Warm up!
∣ x ∣ − 2 ∣ x + 1 ∣ + 3 ∣ x + 2 ∣ = 0 , x = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Very ingenious, but I have a question: do you mean the LHS of the original equation? I can't see why the LHS of the final inequality could not be positive.
Log in to reply
My work shows that ∣ x ∣ − 2 ∣ x + 1 ∣ + 3 ∣ x + 2 ∣ , the LHS of the given equation, is 0 for x = − 2 and it is positive for all other values of x .
First you must determine the zero points: so it's x=0; x= -1; x= -2
The second part of solution is this: You must determinate the intervals maybe like that:
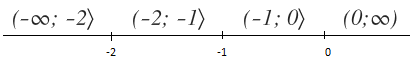
Third part: You need to built a table
maybe like that..
the pluses and minuses means this: example:
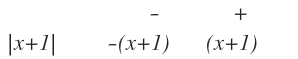
and now you simply make four equations and at the end you must unify results .
Maybe like that:
And if you have a calculator you can do this:
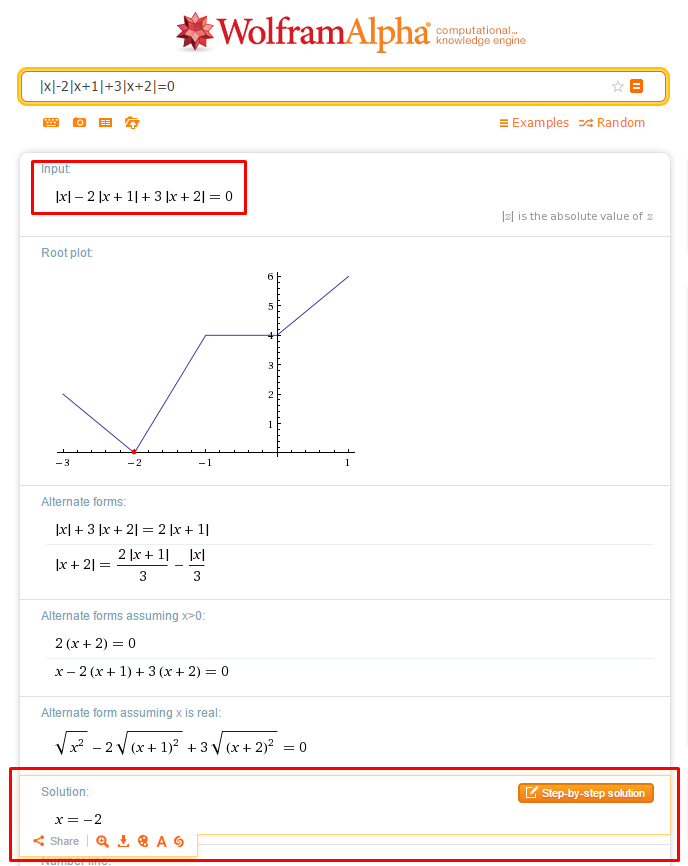
Or maybe using WolframAlpha, or other programs for creating graphs..
By the looks of it, I've got that exact calculator, but how do you solve modular equations with it?
Log in to reply
Do you have casio? If you have it, what model do you have?
Log in to reply
Casio fx -991ES PLUS (in silver)
Log in to reply
@Curtis Clement – I have the same! :D This calculater has a lot of functions. And If you want to solve equations, here is the instruction:
For this example I'll try to solve this easy equation: (x+4)*(x+5)=x^2+29 (^2 this means the second square)
So.. 1) turn on the calculator :D
2) write the equation (by using button - Alpha and button ")" )
3) If you have the left side of the equation, press Alpha and button "CALC" )
4) Now you can write the right side
5) The next step is this: Click on the shift and button "CALC" - so it means the yeallow text - SOLVE
6) press "="
7) And now here we have a solution. :D ...x=1
Do you understand it?
umm... excuse me, can you explain how to read the table? and can you explain how to determine the zero point x=0; x= -1; x= -2 please?
Log in to reply
Hey buddy.. Of course. Do you know how you can determinate the conditions (when you count inequalities)? It's the same. For example, you have this equalities: \left| x-2 \right| +3=5 the zero points, you must only determine from the absolute value! so..
[\left| x-2 \right| \ \ x-2=0\ \quad \quad x=2\quad \Longrightarrow \quad zero\quad point]
you can easyli set the intervals, and n the basis of intervals you setup the table. You add some number from the inerval and place it to absolute value instead the x. like that. you have interval [(-2;-1>] so you can take some number from this interval, I'll pick -1. now you must appoint the number to the table.
[\left| x-2 \right| \qquad |\qquad (you\quad take\quad -1\quad and\quad place\quad it\quad instead\quad the\quad x)\quad \Longrightarrow \quad you\quad get\quad this\quad -(x-2)]
Do you understand, little bit? :D
How to use WolframAlpha.
In the interval (-oo , -2]
|x| = -x , |x + 1| = - x - 1 , |x + 2| = - x - 2
Then
- x + 2(x + 1) - 3(x + 2) = 0
Then
x = - 2 ...............(- 2 belongs to our interval)
In the interval (-2 , -1]
|x| = -x , |x + 1| = - x - 1 , |x + 2| = x + 2
Then
- x + 2(x + 1) + 3(x + 2) = 0
Then
x = - 2 ...............(- 2 does not belong to our interval)
In the interval (-1 ,0]
|x| = -x , |x + 1| = x + 1 , |x + 2| = x + 2
Then
- x - 2(x + 1)+ 3(x + 2) = 0
Then
No solution in this interval
In the interval (0 , +oo)
|x| = x , |x + 1| = x + 1 , |x + 2| = x + 2
Then
x - 2(x + 1) +3(x + 2) = 0
Then
No solution in this interval
Final solution is x = -2
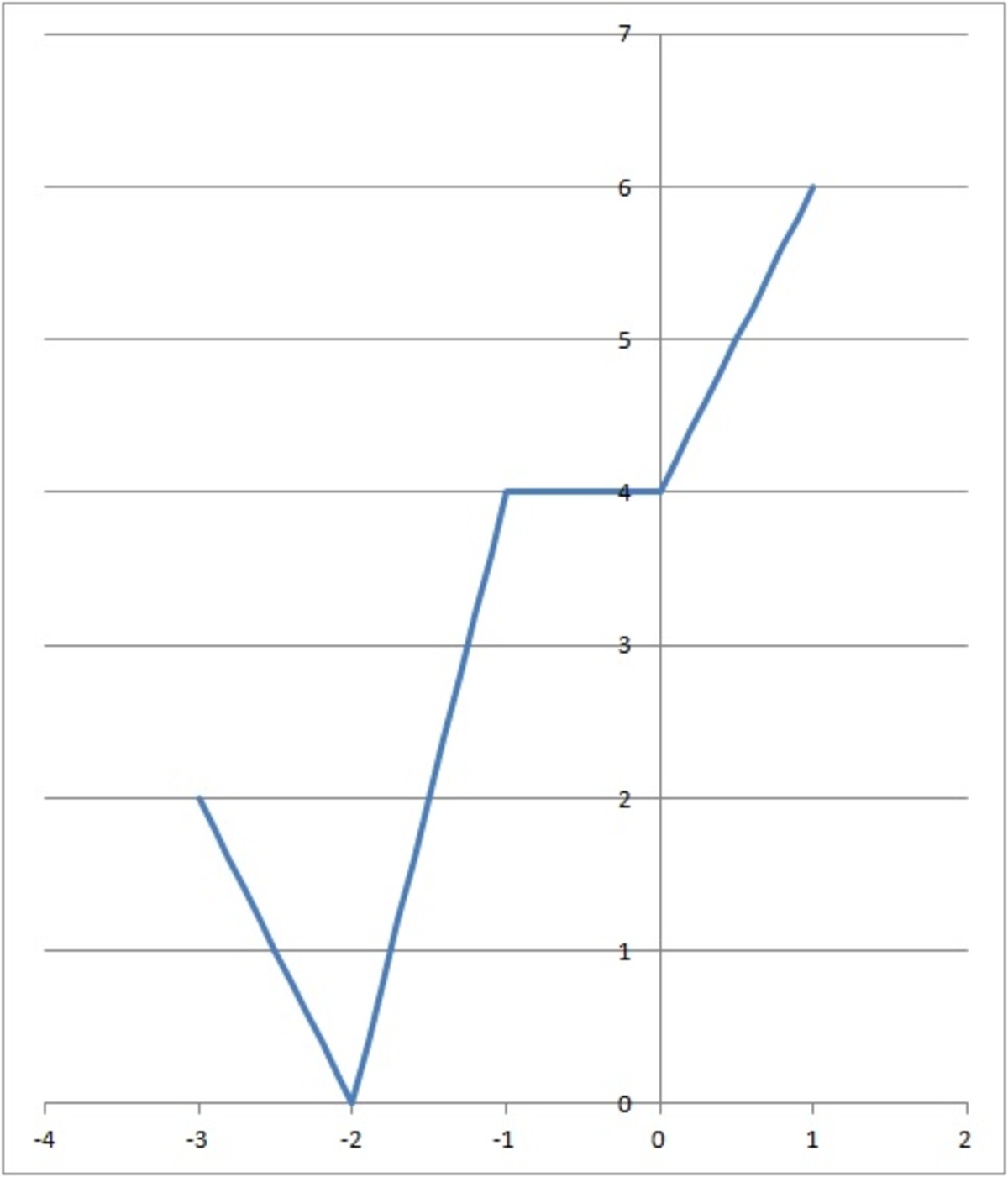
Let f ( x ) = ∣ x ∣ − 2 ∣ x + 1 ∣ + 3 ∣ x + 2 ∣ . Since f ( x ) has three moduli involved ∣ x ∣ , ∣ x + 1 ∣ and ∣ x + 2 ∣ , we have to consider the modular equation in four cases by changing the sign ( + → − or − → + ) with the term involving the corresponding modulus.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ f ( > 0 ) = x − 2 ( x + 1 ) + 3 ( x + 2 ) = 2 x + 4 ∈ ( 4 , ∞ ) f ( − 1 < x ≤ 0 ) = − x − 2 ( x + 1 ) + 3 ( x + 2 ) = 4 f ( − 2 < x ≤ − 1 ) = − x + 2 ( x + 1 ) + 3 ( x + 2 ) = 4 x + 8 ∈ ( 0 , 4 ] f ( x ≤ 2 ) = − x + 2 ( x + 1 ) − 3 ( x + 2 ) = − 2 x − 4 ∈ ( ∞ , 0 ]
Therefore, the answer is x = − 2 .
A graph of f ( x ) confirms the calculation.
| x | - 2| x + 1| + 3|x + 2| = 0 <=>
<=> |x| + |3x + 6| = |2x + 2|
<=> (|x| + |3x + 6|)^2 = (|2x + 2|)^2
<=> x^2 + |6x^2 + 12x| + 9x^2 + 36x + 36 = 4x^2 + 8x + 4
<=> |6x^2+ 12x| = -6x^2 - 28x - 32
For -6x^2 - 28x - 32 > 0:
6x^2 + 12x = -6x^2 - 28x -32 or 6x^2 + 12x = 6x^2 + 28x +32
<=> 3x^2 +10x + 8 = 0 or -16x = 32
<=> (x = -4/3 or x = -2) or x = -2
-4/3 is not a solution of the equation. -2 is solution of the equation.
The only solution of the equation is -2.
I almost did what you did until |x|+|3x+6|=|2x+2| <=> 2x = -4 <=> x=-2 which I then checked since the equation was short and easy.
we can use the triangular inequality ... Or simply substitute the value of x from the given choice
|x|-2|x+1|+3|x+2|=0 x-2x-2+3x+6=0 2x+4=0 2x=-4 x=-2
By the triangle inequality, ∣ a ∣ + ∣ b ∣ ≥ ∣ a + b ∣ , we have ∣ x ∣ + ∣ x + 2 ∣ − 2 ∣ x + 1 ∣ + 2 ∣ x + 2 ∣ ≥ ∣ 2 x + 2 ∣ − 2 ∣ x + 1 ∣ + 2 ∣ x + 2 ∣ = 2 ∣ x + 2 ∣ ≥ 0 . Thus the only possible solution is x = − 2 (for any other x the LHS will be positive), and we can check that x = − 2 is a solution indeed.