Water Droplet Rings
 After a hard rainfall, Bobby decides to go outside to go out to the river behind his house to watch raindrops drip down from the trees above. He notices that a particular tree has one drop fall into the river every second. When the drop hits the water it creates a ring that grows continuously outward at a rate of
π
cm
2
per second. As more drops fall, more rings are created in concentric circles around the drop point. Because the Fibonacci Sequence often shows up in nature, after watching many drops fall and seeing many water rings created, Bobby wonders if there's ever a point in time where there are 6 rings that differ in radius by the first 5 terms of the Fibonacci sequence. An example of what Bobby is thinking of can be seen below.
After a hard rainfall, Bobby decides to go outside to go out to the river behind his house to watch raindrops drip down from the trees above. He notices that a particular tree has one drop fall into the river every second. When the drop hits the water it creates a ring that grows continuously outward at a rate of
π
cm
2
per second. As more drops fall, more rings are created in concentric circles around the drop point. Because the Fibonacci Sequence often shows up in nature, after watching many drops fall and seeing many water rings created, Bobby wonders if there's ever a point in time where there are 6 rings that differ in radius by the first 5 terms of the Fibonacci sequence. An example of what Bobby is thinking of can be seen below.
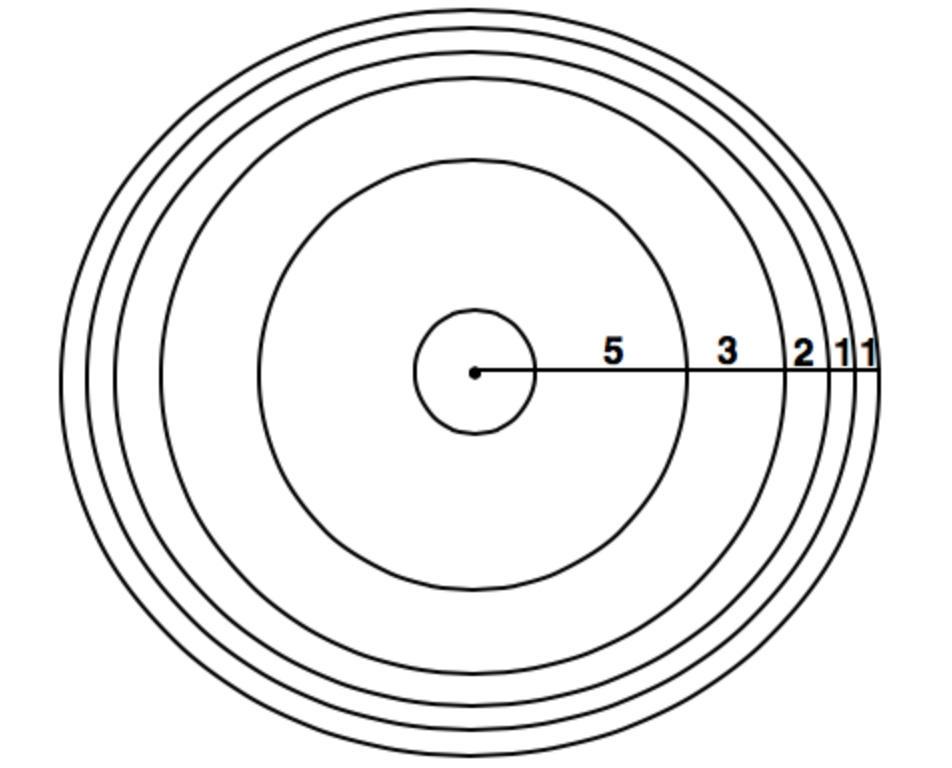
Please note that these rings are not consecutive as shown in the photo; there are other rings of varying radii in between each of the 6 rings.
Bobby soon realizes that there are infinitely many points in time where this can occur, so naturally the question arises: at what point in time does this first occur? If this time can be written in the form b a where a and b are coprime positive integers, find a + b .
Details and Assumptions :
-
Assume t = 0 as the point in which the first drop hits the water.
-
Note that the growth rate is in terms of the area of the circle, not the radius.
-
Circles of radius 0 are not considered circles.
The answer is 629.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very similar to the solution I wrote while making the problem, thank you for posting it and tell your brother I said thank you for his assistance!
Log in to reply
Very beautiful problem, I also thank you Garrett :-) @Morteza Sepehrinia Garrett said thank you for your assistance!
Thanks Garrett
Extension: Prove that for any sequence of differences between circles, the first time when the differences happen satisfies that the radius of the smallest circle r ≤ 2 1 .
Log in to reply
I came across this too while making the problem!
Let r be the time it takes to make the smallest circle and t be the time it takes to make this circle. For positive integers n , m the following equality must hold:
t + n − t = m
t + n = m + t
t + n = m 2 + 2 m t +t)
n = 2 m t + m 2
Our problem requires that n and m be positive integers, which means that 2 m t must be a positive integer as well. We replace t = r :
2 m t = 2 m r
Our problem also requires that we pick t as small as it can be. Minimizing t means also minimizing r . This means that r = 2 m 1 , and m is a positive integer therefore if we let m = 1 we get r = 2 1 , and if there are any greater values of m r will only get smaller, meaning that r ≤ 2 1 for all possible differences. Great question!
Log in to reply
Furthermore, prove that there exists a sequence such that it appears at r = 2 0 1 5 1 .
Log in to reply
@Daniel Liu – I'd actually venture to say that such a value of r is impossible. Take the same formula from above, n = 2 m r + m 2 . We know that if m is an integer, the minimum value is r = 2 m 1 . Since 2 0 1 5 is odd, we know that m can't be an integer. Let's now assume that r = 2 0 1 5 1 is our minimal solution and plug it into our equation.
n = 2 0 1 5 2 m + m 2
n = 2 0 1 5 2 m + 2 0 1 5 m 2
In order for 2 m + 2 0 1 5 m 2 to be divisible by 2 0 1 5 , our minimal value of m is 2 0 1 5 , but look back at our original statement. Plugging in 2015 for m gives us n = 2 ( 2 0 1 5 ) r + ( 2 0 1 5 ) 2 , which has a minimum value of r = 4 0 3 0 1 , a contradiction. Therefore, a minimum value of 2 0 1 5 1 is impossible. Similar methods can be proved to show that any number of the form r = 2 n + 1 1 for n > 0 is impossible.
Log in to reply
@Garrett Clarke – I never said it was supposed to be the minimal solution, but I guess proving that it can't be a minimal solution is a better problem.
Log in to reply
@Daniel Liu – Oh yes, in that case a value of 2 0 1 5 1 is certainly possible. In fact, there are sequences for every rational r that you could choose.
This question was the reason for changing my solution. Regarding the solution I have written: 2 r m i n = max ( a m − a n ) 1 ≤ min ( max ( a m − a n ) ) 1 = 1 r m i n ≤ 2 1
Let r 0 be the radius of the inner ring. Then the outer ring has radius r 0 + 1 + 1 + 2 + 3 + 5 = 1 2 + r 0 .
The time difference between the two outer rings of the pattern of six is of the form ( 1 2 + r 0 ) 2 − ( 1 1 + r 0 ) 2 = 2 r 0 + 2 3 , which must be an integer. This requires r 0 to be a half-integer. Working with other pairs of rings in the pattern yields the same conclusion.
Thus a necessary and sufficient condition is that r 0 ≡ 2 1 mod 2 . The smallest possible value that satisfies is r 0 = 2 1 ; the outer ring therefore has radius 1 2 2 1 , and t = ( 1 2 2 1 ) 2 = 4 6 2 5 . Thus the solution is 6 2 9 .
Best solution.
A lenient/intuitive proof
Let the radius of rings from the inner one to outer one be r 1 to r 6 . (unit: c m )
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ r 1 = x r 2 = x + 5 y r 3 = x + 8 y r 4 = x + 1 0 y r 5 = x + 1 1 y r 6 = x + 1 2 y
where x and y are real numbers
The areas bounded by two consecutive rings are A 1 to A 5 , in terms of π . (unit: c m 2 )
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ A 1 = r 2 2 − r 1 2 = 1 0 x y + 2 5 y 2 A 2 = r 3 2 − r 2 2 = 6 x y + 3 9 y 2 A 3 = r 4 2 − r 3 2 = 4 x y + 3 6 y 2 A 4 = r 5 2 − r 4 2 = 2 x y + 4 2 y 2 A 5 = r 6 2 − r 5 2 = 2 x y + 4 6 y 2
As ring that grows continuously outward at a rate of π c m 2 / s and rings are separated by seconds in integers, the areas are integers.
[Basically next part is matrix reduction using elementary row operations]
Consider A 2 − 2 × A 4 = 9 y 2 and A 4 − A 5 = 4 y 2 , both expression are still integers. Thus y m i n = 1 .
Substitute y = 1 and you will see that x m i n = 2 1 .
Time can be calculated by calculating the area of the first ring = r 5 2 = ( 2 1 + 1 2 × 1 ) 2 = 4 6 2 5
I thank @Morteza Sepehrinia for helping me in solving this problem.
Let A , r and t be area of rings, radius of rings and time respectively.
Growth rate of area for rings is π , hence for each ring A = π t and r = t . Let radius of smallest ring be r , we get r + a k = t k ; 1 ≤ k ≤ 6 ; a k ∈ 0 , 5 , 8 , 1 0 , 1 1 , 1 2 Now the time difference between every two rings is a positive integer, that is if m > n then t m − t n = s m , n ∈ N or ( r + a m ) 2 − ( r + a n ) 2 = s m , n 2 r = a m − a n s m , n − ( a m 2 − a n 2 ) ⋆ To reach the desired condition of problem, RHS of the equation ⋆ must be minimum, which results in minimum r and consequently minimum time where first Fibonacci rings occur.
Now note that a m − a n s m , n − ( a m 2 − a n 2 ) ≥ max ( a m − a n ) min ( s m , n − ( a m 2 − a n 2 ) ) = max ( a m − a n ) 1 ; m > n This is not sufficient, because when equality occurs we have: a m − a n s m , n − ( a m 2 − a n 2 ) = max ( a m − a n ) 1 s m , n = max ( a m − a n ) a m − a n + a m 2 − a n 2 It follows that max ( a m − a n ) ∣ a m − a n for all m > n .
So for any given sequence of natural numbers a k first rings occur for r m i n = 2 ( max ( a m − a n ) ) 1 such that max ( a m − a n ) divides a m − a n for all m > n .
For this problem maximum of a m − a n that divides all of other a m − a n 's is 1 . So r = 2 1 and r + a 6 = t 6 2 1 + 1 2 = t 6 t 6 = 4 6 2 5