Watermelons!
Suppose you have 8 watermelons that are exactly the same in appearance. They are equal in weight except for one, which is heavier than the others. You want to find the heaviest one by using a two-pan balance. Each pan can hold any number of watermelons, and the only items that you can place in the pans are watermelons.
Find the best strategy to determine the heaviest watermelon. In the worst case scenario, how many times do you have to use the two-pan balance?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
"In the worst case scenario, at least how many times do you have to use the two-pan balance?" Doesn't the question ask for the worst case scenario? So doesn't that mean he must try every combination with the other watermelon first before finding the actual one? The tree diagram would be right if it asked to find the heavier watermelon in the least amount of time. (Best case scenario)
Log in to reply
I agree, the phrasing is wrong
Log in to reply
No. Kevin makes the additional assumption that "I can only weight one watermelon against one other watermelon".
Instead, if you look at Sanchayapol's solution, you will see that the first step involves weighing 3 watermelons against 3 other watermelons. If the pans are balanced, then we can eliminate 6 watermelons in the very first step.
The question means the worst case scenario for your method. Ex. If you weighed each melon against the first until you had one that was heavier, in the best case scenario, one of the first two melons that you weighed would have been the heavier one, hence without this clarification the answer would be 1. With the phrasing, you must take the worst case scenario which would be the 7th or 8th melon would be the heaviest, thus taking 6 trials. The best method for the worst case scenario is as Sanchayapol outlined, where any scenario takes 2 trials.
Agreed. The phrasing on this question is unclear at best.
By using 3 on each side and leaving 2 off it doesn't matter. If the 2 balance than it is one of the 2 left off in which case you can determine that using the two arm scale. That would be two steps. If the 3 don't balance in step 1 then you know it is going to be three that on the arm that is higher. In that case you put one on each side of the scale and leave one off. If one of the arms is higher than the other than that one is lighter and if they balance and you know that the one you left off is lighter . Either way it's only 2 steps
And what is wity watermelon 7 and 8?
The question also says "the best strategy" ... The best strategy is the one that "logically" gives you the answer in minimum attempts .. Comparing 1 watermelon each on one pan would not even be a strategy .. I did the same in the beginning but understood later on when my answer "4" went on to be incorrect
Agreed. The answer is 6. In the "worst case scenario" you use the least effective method, which is weighing one individual against the rest. So: 1v2, 1v3, 1v4, 1v5, 1v6, 1v7. In the worst case for this method, all so far are equal weighings, so you have yet to weigh the heaviest mellon. Hence, the 8th is the heaviest and you have weighed 6 times.
Log in to reply
The "worst case scenario" is if your "best method" requires its maximum iterations to complete. The point is to choose the method that, at its least efficient chance, has the fewest measurements.
If you measure each watermelon against the first watermelon, the worst case is that the last measurement, i.e., the sixth measurement, shows you which watermelon is heaviest. Then again, that disregards the fact that after five weighings, having not found the heavy melon, you can deduce that the unweighed melon is the heaviest.
If you measure the melons in pairs, 1v2, 3v4, 5v6, 7v8, the worst case is that either the 7th or 8th melon is the heaviest, which thus takes 4 measurements.
If you measure two pairs of melons at a time, i.e., 12v34, 56v78, then measure the heavier pair against each other (1v2 or 3v4, or 5v6 or 7v8), then you're down to three measurements. since the third weighing will be sufficient to declare the heaviest melon.
The "best method", then, is to measure 123v456, then all that's left is 1v2, 4v5, or 7v8. The worst case of the best method is two measurements.
Maybe the worst case scenario is the capability of the balance to be used with specific times only.
no.... you might not understand it.... but this is my understanding.....
First of all watermelons 1,2,3 _ 456
case 1: if 1,2,3 > 4,5,6, then the heavier one is on 1,2,3 .... eliminating 4,5,6,7,8
case 2: if 1,2,3 < 4,5,6, then the heavier is on 4,5,6.... eliminating 1,2,3,7,8
now the remaining three watermelons, two have the same weigh while ONLY one is heavier... there are only three possibilities:
a. 1 > 2 then 1 is the heaviest b. 2 > 1 then 2 is the heaviest c. 1 = 2 then the remaining no. 3 watermelon is t
Not true. You are making the assuming that we can only place one watermelon into one pan.
Even if you're restricted to weighing one watermelon against the other, in the first round if it's balanced, you can eliminate both of them. Hence, we just need to do 1v2, 3v4, 5v6, 7v8, which means a max of 4 weighings instead of 6.
No, you don't have to weigh every pair of watermelons against each other.
For example, say we weigh water melons 1 and 2, against 3 and 4, and the pan is balanced, then we know that none of these are the "heavier watermelon".
The phrasing is not wrong. Read the solution carefully. It tells you the solution of each possible case.
It depends on how much heavier the heavy one is- in your solution (Case 1.3) you assume that the heavy one is 2 times as heavy as the regular ones- but you don't need the pans at all. You would feel the heavy one as you put it in the scale.
Log in to reply
Where are you seeing that he assumes the heavier melon is twice the weight of a normal one? That's not stated anywhere in his solution. I think his method of using numbers to refer to the watermelons has confused you.
Instead, call the watermelons A, B, C, D, E, F, G, and H.
-First, weigh A, B, and C against D, E, and F.
Case 1: the A, B, C side is heavier, so you know that A, B, or C is the heavy melon.
-Then, weigh melon A against melon B.
Case 1.1: Melon A is heavier than melon B. Thus, melon A is the odd one.
Case 1.2: Melon B is heavier than melon A. Here, melon B is the odd one.
Case 1.3: Melons A and B are equal in weight. This means that neither A nor B is the odd melon, so melon C must be.
Case 2: The D, E, F side is heavier, so you know that D, E, or F is the odd melon.
-Here, just repeat the process outlined in Case 1, using D, E, and F instead of A, B, and C.
Case 3: The A, B, C side is balanced with the D, E, F side. This means that the heavy melon must be either G or H.
-Here, simply weigh G against H. The heavier one here will, of course, be the odd melon.
There was never any assumption about how much more the 'heavy' melon weighed compared to a 'normal' melon.
Yes. Information theory can tell you have many times you need the balance. The first thing you do is find out how much information is contained in knowing which is the heavy watermelon. Since this is one of eight, the amount of information is: -log2(1/8) = 3 bits.
The next thing to work out is how much information you get each time you use the balance. There are three possible outcomes: 1) left side drops, 2) right side drops, and 3) neither side drops (equal weight on both sides). So the amount of information the balance gives you is: -log2(1/3) = 1.585 bits.
Since the information in knowing which melon is heavier is 3 bits, and the information the balance gives you is 1.585 bits (rounded), the theoretical minimum number of times you need to use the balance is 3 / 1.585 = 1.893 times. Since you can't use the balance a fractional number of times, this says you need to use it twice to find the heavy melon. So you actually don't even need to solve the problem to answer the question!
The fact that you're using the balance twice when theoretically you need it only 1.893 times implies that there may be alternate solutions to the problem. There's another (harder) version of this problem where you have twelve coins that all look the same, but one is fake and you don't know whether it's lighter or heavier, only that it's weight is different from the eleven real coins. And you have only three chances to use the balance. It turns out there are at least two solutions to that puzzle, because theoretically you only need to use the balance 2.262 times.
Kevin Kazami, actually the solution is correct-you only need to use the scale twice
Since the question asks you to FIND the heaviest watermelon, if the second test is balanced, you need a third weighting against any other watermelon to verify the heaviest watermelon, otherwise you are ASSUMING the last watermelon is the heaviest (mathematics never assumes, it determines). The "worst case" scenario requires 3 tests, not 2.
Log in to reply
This is engineering, not mathematics. You already know that one of the watermelons is heavy; you have to deduce which one.
The only problem that could be argued with the wording is that the worst case scenario and best case scenario are identical. Having said that, it needs to be mentioned otherwise some fluke could pick up the right melon straight of the bat and compare it individually. That worst case scenario would be 7.
Log in to reply
Even you are restricted to place one melon per pan, you still can do it in 4, or 1v2, 3v4, 5v6 and 7v8
I got tipped of by the term "worst case scenario" so I thought it meant the most number of tries you might need.
I think the answer should be 3 when asked for the worst case with the best method. Divide the mellons in 2 groups of four (weighing 1). Divide the heaviest group in 2x2 (weighing 2) and then idealy you can use your hands to decide which of the two in the heaviest pair is the heaviest. In the worst case you would use the scale for a third time (weighing 3). So I think either the "correct" answer of two is wrong or the question about the worst case is wrong and should be about the luckiest case...
Log in to reply
One of the assumptions in a scales problem like this is that you're only allowed to make weight assessments using the scales themselves, so "using your hands to decide" isn't allowed in the solution.
Sanchayapol Lewgasamsarn posted an explanation of how the weighing can be guaranteed complete in two weighings.
Should be worded. . . . other than picking up two random watermelons & weighing them and the the heaviest tips the scale (one time =1) what is the fewest amount of times you would have to use the scale to determine the heaviest watermelon? 2, 3, 4, 5, 6, 7, 8, etc. I understood the question as worded before . . . sorta, and thought it would be three. I was wrong it is two.
Why r watermelons 7&8 untested? There isn't a definite proof the other 2 remaning are lightest
To me the answer is 3 times. I put 1 2 3 4 and 5 6 7 8 in two pans. If 1 2 3 4 pan is heavier than the heaviest watermelon is in there.
Now i put 1 2 and 3 4 into two pans. If 1 2 is the heavier than the heaviest one is in there.
Now, i put 1 and 2 into two pans and finally get the heaviest watermelon from the heavier pan.
you said 1,2,3 and 4,5,6 but the amount of watermelons are 8 ,so where did the remaining 2 go?
Log in to reply
Read on.
Case 3 deals with the case where the pan is balanced, which tells us that one of the remaining 2 is the heavier watermelon. Case 1 and 2 deal with the case where the pan is unbalanced, from which we can determine that the heavier watermelon is one of the first six.
Log in to reply
i get confuse, did question mention 3 combination in each pan? so how everyone know 3 watermelons in pan but i cant find
Log in to reply
@Wai Keong Ho – You can place any number of melons on each pan.
There are 8 water melon so surely you put four in one pan, and four in the other which ever one ways more you know has the heavier one. you then divide this again so 2 in each, then divide the heavier side again to work out the finally stage. (although this would be for the best possible scenario) the worst would be work out by comparing each one individually as this could potentially lead to 7 trials.
Also the answer 2 doesn't work as they try the solution more than twice.
Log in to reply
That is the correct analysis for the worst case scenario in the specific strategy that you chose.
With the phrasing of "at least how many times", the question is asking for the worst case scenario for the best performing strategy,
The answer is 3.
You put 4 melons on each side. 1 side will be heavier. You discard the 4 melons on the lighter side. You now split the remaining melons in half and weigh 2 on either side. Once again one side will be heavier. Discard the 2 melons on the lighter side. You now have 2 melons, one one either side of the scale. You have now found the heaviest in 3 uses of the scale.
Log in to reply
I would suggest you to look at other solutions which will give better performing strategies.
The solution is not matching the phrasing of the problem. The problem says: "in the worst case scenario, at least ...". "The worst case scenario" means the brute force search, which comparing one with the rest. But the solution considers "the Best case scenario"! I suggest to rephrase the question to: "What is the minimum number of times one could use the two-pan balance to find the heaviest watermelon?"
Log in to reply
No. In the best case scenario, you only need 1 weighing to find the watermelon.
It is "in the worst case scenario", where you are supposed to find the "best approach to minimize".
You're confusing "worst method" with "worst case scenario".
Log in to reply
The worst method is weighing the first four vs. the remaining four, without ever changing the grouping. You'll never be able to find out which one is heaviest. Or if there has to be a guaranteed solution in as many different weightings as possible, start with 8 vs. 0, then do all combinations of 7 vs. 0, ..., 1 vs. 0, then 7 vs. 1, 6 vs. 1, ..., 2 vs. 1 (intentionally skipping 1v1), 6 vs. 2, ... etc. As long as the heaviest melon is less than twice as heavy than the others we can do a lot of weightings with known outcome before we get to weightings which might reveal the heavier one. If we do a 4 vs. 4 weighting, we can determine 4 normal ones and do all possible weightings with those before we further narrow down which one is the heaviest.
It definitely sounds like an interesting math problem to determine the highest number of weightings you can do without repeating weightings (weighing A vs. B and weighing B vs. A are identical), and without determining the heaviest melon.
Also, the brute force search can be waaaaaaay faster than that. Just do 1v2, 3v4, 5v6 and 7v8.
Why isn't the answer 1 time using the balance?
Place 1 melon on each side, if different you have your answer, if same add 1 more melon to each side (since its still balanced) and keep going until you have one side heavier.
Log in to reply
When you do "if same", you are already doing one weighing.
As you "keep going", that's more weighings.
Since the question mentioned that the pan can hold any weight, why not we take the worse case scenario such as 4 watermelons for each side at first go, then take heavier side and weigh 2 each for the second time, and same goes for the third time? The answer will become 3. Correct me if I'm wrong please.
Log in to reply
We want the best strategy with the worst case scenario. So the method said in the answer is more efficient than this method.
The answer is 2.
Take 3 on each pan. If they are same then put rest two on pan and compare. If in first case weight of any 3 watermelons is greater then keep one at a side and rest 2 on the pan. If they are equal then the third one is the answer and if one of them it will ne shown on the pan So the answer is 2.
You are wrong i guess because, there are eight watermelons and your are using 6 only (3-3) what is the heaviest watermelon is between the other 2 left. So i think that the we need to check three times.
First time== divide watermelon 4-4 and check the heavier side then between that the side which is heavier dived that into 2-2.
Second time== divide watermelon 2-2 and check the heavier side and then divide watermelon into 1-1.
Third time== divide watermelon 1-1 then you will get to know the heaviest watermelon . . .
Log in to reply
He accounts for the case that one of the heavy melons is not one of the first six he weighs. In that case, the first measurement comes out equal, and he measures melon 7 against melon 8.
"Worse case" is completely unclear
Log in to reply
"Worst case" is completely clear. "case: A set of circumstances or a state of affairs". It means, in the event that you don't get lucky and find the heavier melon on your first try, how many tries will it take to actually logically ascertain which melon is heaviest?
I believe 3 because it's worded that watermelons may only be placed in pans. This could mean that you must have all 8 in pans at all times. In which case:
1) You have 4 on either side. Call the 4 lighter melons "L's" and the 4 heavier melons "H's".
2) You swap 2 H's from the heavier side with two L's from the lighter side. The H's on the new lighter side become L's, and you have only 2 H's remaining on the heavier side.
3) Then take one of the two H's and swap with one of the L's on the lighter side. The H on the new heavier side is the heaviest.
Log in to reply
It's not saying that you must have all 8 watermelons in the pans at all times, it's saying that you can only count measurements that are made using the scale, i.e., you're not allowed to gauge the weights of the watermelons by hand.
Exacto. Si la pregunta está mal formulada no tiene merito encontrar la respuesta. El peor escenario seria ir midiendo de dos en dos y que al final aparezca el correcto. En ese caso la respuesta seria usar la balanza 4 veces.
First we put 4 watermelons on both sides. Then out of them one side will be heavier as the heaviest is on that side. Now we will take 2 watermelons on both sides. Out of them, one side will be heavier as the heaviest is on that side. Again we can compare both sides and so we will use it 3 times.
The green vertex (green box) is the first step.
The blue vertices (blue boxes) are the second steps.
The red vertices (red boxes) are the conclusions.
The edges (black lines) show the results of each step.
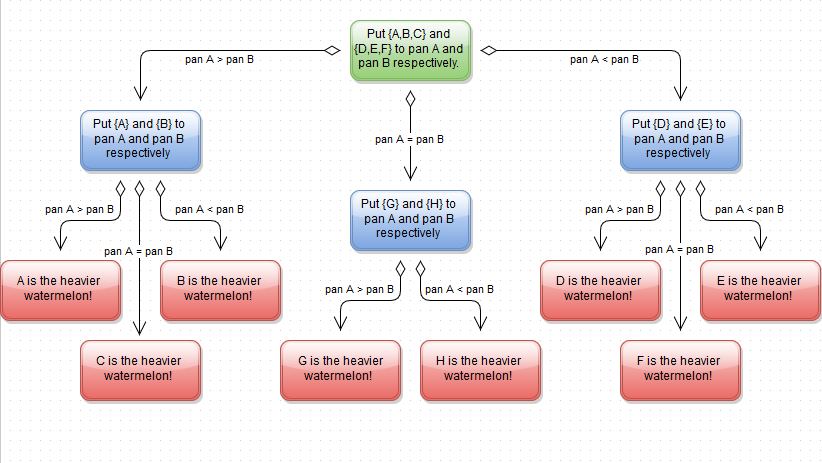
I agree................ Nice come up plan
Sorry to necro, but this is gorgeous. What software did you use to make this map?
Log in to reply
Has anyone pointed out that you don't need to consider cases for the second weighing?
123 vs 456 147 vs 258
works regardless of the result of either weighing.
Log in to reply
Yes that does work but you have to identify the watermelons for the benifit of others spell out what conclusions the results of this weighing will lead to.
Log in to reply
@Zahid Hussain – Sorry, in the second line it should be "...watermelons, and for...
I had a plan, but this beautiful.
Good diagram that fully explains it. Might be easier to understand if you called the watermelons 1,2,3 . . . 8 OR called the pans pan 1 and pan 2.
- take out any two melons.
- put the rest of them onto the pans 3 on each side.
- if they are balanced, the heavier is one of the two you already separated and hence one more weighing will identify it.
- and if they are not balanced, the heavier pan contains the required melon, take one melon that you doubt to be the heaviest out of the three. and do a second weighing, if they get balanced, you have it, otherwise the heavier pan has it.
I understood this answer more clearly! 😃👍🏻👍🏻
I have a doubt regarding 4. if they are not balanced, how can you doubt which is heaviest of the three? They look all exactly the same. If you remove 1 watermelon from both sides and if the pan balances, you would know which one is heaviest. If they still unbalanced then either of the two watermelons on the heavier side can be the heavier one os you would have to do a 3rd measurement. Your strategy's worst case scenario implies 3 steps Then how do you predict 2?
Answer must be 3
It should be 3 times because the question clearly states that melons can only be placed in the pans. This means that we can't have melons on the ground or anywhere else, hence we have to place all 8 melons in the pans during the whole process of determining the heavier melon and we can only swap melons between the two pans.
So: Lets number the melons 1,2,3,4,5,6,7,8 (lets assume 1 is the heavier one)
1st: place 4 melons in each pan (1,2,3,4 and 5,6,7,8). Pan1 will go down because it contains the heavier one.
2nd: swap two melons from each pan. Chase1: You swaped the heavier one (5,6,3,4 and 1,2,7,8) so pan2 will go down. Chase2: You didn't swap the heavier one (1,2,5,6 and 3,4,7,8) so pan1 will stay down.
3rd:
In chase1 swap one of the melons (1 or 2) back. If pan1 goes down again the melon you just put back is the heavier one. If pan2 stays down the melon you didn't put back is the heavier one.
In chase2 swap one of the two melons from pan1 that you haven't put in pan2 yet (1 or 2). If pan2 goes down you just put the heavier one there. If it doesn't the heavier melon is the melon you left in pan1 the entire time.
You've misread the question. It does not say the watermelons can only be in the pan; it says the pan can only take watermelons ("and the only items that you can place in the pans are watermelons").
You do not have to have all the watermelons in the pan at once.
Log in to reply
I had the same suggestion, it would mean in our case that it should be 4 times since for each watermelon separately at last the 7th or 8th will measure the heaviest.
The pan has to weigh separately on each scenario.
That only means you cannot weigh anything other than watermelons on the pans. You do not have to weigh all 8 watermeleons each time.
divide 8 watermelons into 3 groups of 3-3-2 (call them group A, B, C).
-
Weigh group A and B. If they are balanced => C has the one.
-
Weigh 2 watermelons of group C we will find the heavier.
2'. If A and B are not balanced, weigh 2 watermelons of the heavier group. If they are balanced then the answer is the other. If they are not, we can easily see which is heavier.
Wonderful explanation
There is a problem with the question. It states that "You can only place watermelons in the pan". Therefore, you cannot leave watermelons out of the pan as mentioned in most solutions. This requires that a third weighing in needed.
unless the original wording has changed, "Each pan can hold any number of watermelons, and the only items that you can place in the pans are watermelons" doesn't prohibit watermelons from being anywhere other than the pan.
That being said, it would be realistically difficult for one person to be putting in more than one watermelon at a time on either side of the scale, and the heavier one would be located while loading up each side, one by one.
The wording clearly suggests that only watermelons can be placed on tge pans meaning not anything else. Suggests nothing about requiring weighing of all 8 watermelons each time.
This is a much repeated question, just with different things written in a different way. In fact, in this quiz there are 3 questions that are the same!! The real answer is 2, because you can split the 8 water melons into 3 sections. 1 2 3, 4 5 6, and 7 8 . We weigh 123 and 456. If they are egaul which 7 and 8. Then see, that is 2 steps. Some problems however, have the answer of 3. Accluty, my first statement was wrong. 2 questions are the same with different answers. That's weird....
It is a pity they are 8. They should be nine. Still two is the answer.
First, weigh three in each pan. If one pan is heavier, set those three aside, then weigh two of them to see which is heavier. If they are the same weight then the third watermelon is the heavier one. If the first weighing balances, then one of the two watermelons that weren't weighed the first time must be the heavy one. Weigh these two to find out which one is heavier.
You said worst case scenario... so my solution is, divide the 8 into two pans, then whatever is the heaviest holds the heavier one... which leaves me with 4 watermelons... same process leaves me with 2 watermelons... then whatever is heavier then it is the watermelon
Look at other comments for better strategy
At first I thought the purpose of this case is the combination (1-2, 2-3, 1-3, etc) with a special treatment (8C2 - 6 = 56 - 6 = 50 times, because my initial assumption be only one watermelon in the each pan, where specifically taken only one time of 7 times the chance of occurrence pair of watermelons in which there is the heaviest watermelon)
But some time later, I realized that my answer was not confirmed. Moreover, having considered the statements in question "Each pan is very strong that they can hold any weight in the world", which means each pan can be filled watermelon as much as possible. So, maybe I agree with Kevin Kazami on "best case scenario" for the construction of the question, it's not "worst case scenario", although I finally understood what the question's Sanchayapol Lewgasamsarn.
So, the best opportunities ("best case scenario") is to put 3 watermelons to each side of the pan, because then we would get just one clue needed to identify the heaviest watermelon.
By placing 3 watermelons for each side pan of 8 watermelons as a whole, then 2 times by using the scales have been able to find a watermelon heaviest, despite a worst-case scenario "as referred Sanchayapol Lewgasamsarn, when each 3 watermelons on both sides of the pan have the same weight, so that only the scales used for the two remaining watermelons (still only requires two times using the scales cumulatively)
divide them 6 to 2 ..
1-weigh the 6 .. 3 against 3
if
2-they balance weigh the remaining 2 against each other
2-they not take the heavier 3 and pick 2 of them to weigh against each other
2.1-if they balance the excluded is the heavier
2.2-if not the one bottoms is he heavier
the total number is 2
step 1: put 4 watermelon on each side, pan will always be unbalanced. Not take out 1 watermelon form each side, say A and B
step 2: if pan is unbalanced it means A and B are of same weight, put them aside and go to step-1 if pan is balanced, compare A and B's weight on pan and repeat the process.
Since it is asked the least time we need to use the pan, number is 2
I believe the question meant to ask at least how many times to guarantee to find out the heavier one, if its so, in this case your answer is wrong because it cant be guarantee that in 2 weighing, the heavier one can be found. If not, based on your logic, i can just weigh 2 by 2 and the least is 1 weighing if i got lucky the first pair i found the heavier one. So your explanation is wrong.
I guessed 3, then 4, then 2, wondering why 3 was wrong. I understand why now.
- Split items in three groups: G1 (three items), G2 (three items), G3 (two items).
- Compare G1 vs G2.
- If pan is in EQUILIBRUM, compare items of G3 where heavier is the RESULT.
- If pan is not in EQUILIBRUM, take heavier group and continue.
- Compare first and second item.
- If pan is in EQUILIBRUM, then third item is the RESULT.
- If pan is not in EQUILIBRUM, then heavier is the RESULT.
Maybe the general optimal solution is to split remaining group in three and continue with the heaviest group recursively
If we place 7 on one side and 1 on the other, since we're assuming worst case scenario, the pan with the 7 will outweigh the other one. So it would take more than 1 try. I'll start with an observation: it's easy to think about splitting them with 4 and 4. I did some mental experiments with this strategy of splitting into equal parts (got an upper bound of 3 and since we have 3 tries, then I was gonna get the problem right by guessing) and got that the best strategy would be to place 3 and 3.
C a s e 1 They balance out. Then the heaviest one is between the 2 that we did not weigh. weight just those 2 and this will tell us which one is the heaviest.
C a s e 2 They do not balance out. Then the heaviest one is among one of the 3 and we will know which 3. Take 2 of them from that group and weigh just those 2. We have 2 sub-cases. (a) they weigh the same and so the one we did not weigh from that group is the heaviest one. (b) they weigh differently and we have the heaviest one.
Suppose x stands for each watermelon and the balance looks like this. ----- _ _ -----
First, place 3 watermelons on each side and leave the last two. xxx xxx ----- _ _ ----- xx
Next, if one of the sides is heavier than the other, keep the three watermelons on that side and clear the rest because you know that one of these three watermelons is heavier than the others. Put one watermelon on each side and leave one. x x ----- _ _ ----- x
If one side is heavier than that is the heavier watermelon. If it is balanced, then the watermelon that you left on the side is heavier.
There's also another way, when your balance looked like this: xxx xxx ----- _ _ ----- xx
If the sides were balanced, then the two watermelons on the side contained the heaviest watermelon.
Clear the balance except for the two watermelons and put one of the two watermelons on each side. x x ----- _ _ -----
The heavier side is the heavier watermelon.
Therefore, using any of the two ways, you would only have to use the balance two times, so the answer would be 2.
Sorry if this is confusing, I am only a 6th grader, so I can't explain it as well as other people. (Something went wrong with the balances.)
Wouldn’t 2 (being the very least number of times needed to use the balance) be the BEST case scenario? My answer was 8 because it asked for the WORST case. Does that not typically mean the least optimal solution? Compare the first to every other until you see a difference. Worst case, you check one against all others and find that the seventh comparison is the one with the heavier watermelon.
The question wants the BEST strategy for the WORST case.
In "the worst case scenario" one assumes the person trying to find the heavier watermelon is ignorant and balances them 2 at a time with one on each side, and not only being ignorant is unlucky enough to take 4 tries to find the heavy one.
It doesn't assume the person who did the balancing is stupid enough to get LITERRALLY the worst case. It want the BEST method in the worst case.
Solution
Divide 8 to 6-2
Then 6 to 3-3
Now if those weigh the same then you can weigh the two and find out.
But that's not the worst case scenario.
Step 1
In the worst case you will have 3 watermelons left.
Divide it in 2-1.
Step 2
Now weigh the 2.
In the worst case either both weigh the same or one of them is heavier.
Then you can find out the answer in 2 steps.
Let's say our set is {L, L, L, L, L, L, L, H}. Let's take a total of 6 From the set. The two possible cases are that both sides are equal or that one side weighs more than the other. If both sides are equal, then we just take the 2 we didn't use from the set and see which side is heavier. This case took 2 weigh-ins overall. Let's look at the other case: We know that the heavier watermelon must be on the heavier side, so let's remove the other side and the other two melons we didn't use from the set. Now, if we just take two watermelons and put one on each side, one case would be that they weight the same which would mean the one we didn't use is the heavier one. The other case would be that they don't have the same weight which then the heavier side is obviously the heavier watermelon. This case took 2 weigh-ins overall. As we can see, we end up with 2 as the worst case scenario in the final outcomes, so the answer is 2.
Its easy to extend this to prove that you need x = ⌈ lo g 3 n ⌉ measures to locate the heaviest watermelon. Since the outcome of each measure has three diferent values, if 3 x < n there is not enough different measures outcomes to discriminate the watermelon. An optimal strategy is to measure n / 3 against n / 3 watermelons. If they are equal, the other n / 3 watermelons contain the heaviest. If they are different, the heaviest n / 3 watermelons contain the heaviest watermelon. Recurse :)
This can be solved in many ways but I'll show you the general way. Let 1, 2, 3, 4, 5, 6, 7, 8 be the eight watemelons.
In every cases, it's at least 2 times.
I still haven't got a proof which proves that the process cannot be completed in a time. Does anyone have one?