Weight And Springs

Classical Mechanics Level 5

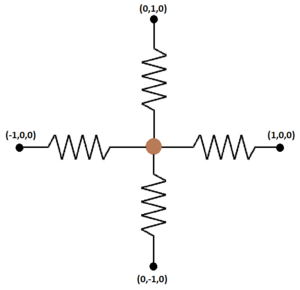
In the $xyz$ -coordinate system, there are 4 fixed (immovable) points at $(x,y,z) = (\SI{1}{\meter},\SI{0}{\meter},\SI{0}{\meter}),\ (\SI{0}{\meter},\SI{1}{\meter},\SI{0}{\meter}),\ (\SI{-1}{\meter},\SI{0}{\meter},\SI{0}{\meter}),\ (\SI{0}{\meter},\SI{-1}{\meter},\SI{0}{\meter}).$ There is a movable $\SI{1}{\kilo \gram}$ mass attached to each of the 4 fixed points by a spring of spring constant $k = \SI{1}{\newton \per \meter}$ . The mass is initially at rest at $(x,y,z) = (\SI{0}{\meter},\SI{0}{\meter},\SI{0}{\meter})$ , and the springs are initially un-stretched.

The mass falls under the influence of gravity $\big(\SI{10}{\meter \per \second \squared}\big)$ in the $-z$ direction of the springs. When air resistance eventually brings the mass to rest at an equilibrium position, how far (in meters) is the mass from the origin (to 2 decimal places)?

Note: All quantities are in standard SI units.

The answer is 3.46.

1 solution

Pranshu Gaba
Oct 23, 2016

When the mass finally stops moving, it will be in equilibrium. Its weight will be balanced by the components of the spring force. The spring force depends on the extension of the spring. From the above diagram, we can see that the original length of the spring is $\SI{1}{\meter}$ , and the final length of the spring is $\frac{1}{\sin \theta}$ . The extension of the spring is $x = \frac{1}{\sin \theta} - 1$ .

The component of the spring force in the vertical direction is $k x \sin \theta = k (\frac{1}{\sin \theta} - 1) \cos \theta$ . Since there are 4 springs, the total upward spring force on the mass is $4 k x \sin \theta$ . This should be balanced by the weight of the mass, therefore

$mg = 4k \left(\frac{1}{\sin \theta} - 1\right) \cos \theta$

We can solve this using WolframAlpha, and the only solution we get for $0 < \theta < \frac{\pi}{2}$ is $\theta = 0.2813...$

The height by which the mass is lowered is $h = \cot \theta \approx 3.461\ldots$

But wouldn't that be below the lowest fixed point ? Is the gravity that much stronger than 4 springs, including top one being stretched over three times it's initial length?

Brian Kelly - 4 years, 7 months ago

Gravity is into the page, not down the page.

Steven Chase - 4 years, 7 months ago

Oops. Thanks much, I see that now.

Brian Kelly - 4 years, 7 months ago

Although i have solved it still i've confusion in wordings of the problem. At the equilibrium position mass won't be at rest will it be? . or the meaning of problem is something else?

Prakhar Bindal - 4 years, 7 months ago

It will eventually be at rest at a point where the sum of the forces is zero (after air resistance brings it to a stop).

Steven Chase - 4 years, 7 months ago

But that isn't the case . if we release a spring block system from rest the mass will be at rest a distance 2mg/K From unstretched position while the equilibrium position will be a distance mg/K From unstretched position.

Where m denotes mass of block , g is acceleration due to gravity and K Is stiffness constant of spring

Prakhar Bindal - 4 years, 7 months ago

@Prakhar Bindal – How are you defining equilibrium? As the point where the net force is zero?

Steven Chase - 4 years, 7 months ago

@Steven Chase – Yep i suppose it is defined that way only!

Prakhar Bindal - 4 years, 7 months ago

@Prakhar Bindal – Yeah, so then the answer to this question is that number. Of course, the mass will descend lower than that point during its transient period. But it will eventually settle there, given losses such as air resistance.

Steven Chase - 4 years, 7 months ago

Weight And Springs

The answer is 3.46.

1 solution

0 pending reports