Weird construction

Geometry Level 4

Given a triangle $ABC$ with circumcenter $O$ , how many moves does it take to draw a line $\ell$ through $O$ where $\ell$ intersects $AB$ and $AC$ at $P$ , $Q$ such that $PO=OQ$ ?

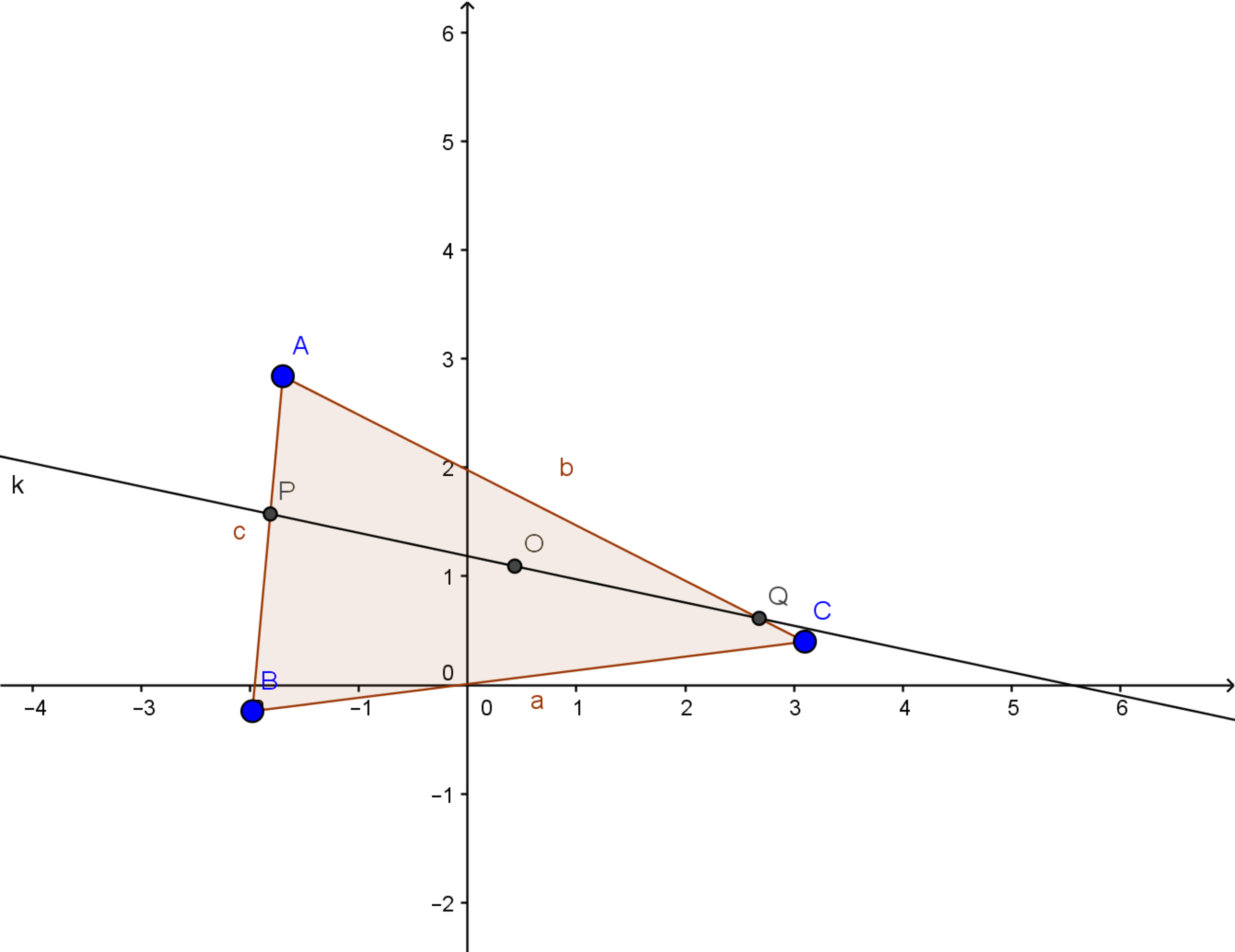
All terminology in this question is explained in the first note of my straightedge and compass set. More straightedge and compass constructions can be found there.

5 Not possible 6 7

1 solution

Wen Z
Nov 16, 2016

I'm not sure if there's a shorter solution

Can you please supply a proof of why this is true?

Sharky Kesa - 4 years, 6 months ago

Really vague proof outline, but all the steps should be quite simple:

Prove that there does exist such a line
Letting E be the other poing of intersection between AO and the circumecenter, prove that AQEP must be a parallelogram
Prove that AB||DE as shown in the diagram
Now to finish prove that AP||QE is sufficient

Wen Z - 4 years, 6 months ago

I like the fact of $AQEP$ is a parallelogram. I think you can use that to make a much more interesting question (and especially one that doesn't rely on there not being a shorter approach to this construction)

Calvin Lin Staff - 4 years, 6 months ago

@Calvin Lin – Well I got the inspiration from an Olympiad training problem: given $E$ above, let the tangent at $E$ intersect $BC$ at $X$ . Prove that if $XO$ intersects $AB,AC$ at $P,Q$ , then $O$ is the midpoint of $PQ$ .

Wen Z - 4 years, 6 months ago

@Wen Z – Oh, the proof of the fact is easier than that.

From A, construct the diametrically opposite point E. Then, draw lines from E that are parallel to AB, BC. This forms a parallelogram, with intersection points of P and Q. Since the diagonals of a parallelogram bisect each other, hence we are done.

Calvin Lin Staff - 4 years, 6 months ago

@Calvin Lin – What I mean is that I realised it would be a parallelogram when attempting the Olympiad problem and made the question.

Wen Z - 4 years, 6 months ago

Weird construction

1 solution

0 pending reports