Weird Land for Sale

Let the side of the square be 1.

Because $\Delta AEF$ is equilateral and symmetrically drawn in square $ABCD$ we know that $\angle DAE = \angle BAF = \dfrac{90^\circ-60^\circ}{2} = 15^\circ$ (see figure made by Worranat Pakornrat).

Because $\sin(45^\circ) = \cos(45^\circ)$ we know that:

$DE = \tan(15^\circ)$

$= \dfrac{\sin(15^\circ)}{\cos(15^\circ)}= \dfrac{\sin(45^\circ-30^\circ)}{\cos(45^\circ-30^\circ)}= \dfrac{\sin(45^\circ)\cos(30^\circ)-\sin(30^\circ)\cos(45^\circ)}{\cos(45^\circ)\cos(30^\circ)+\sin(45^\circ)\sin(30^\circ)}= \dfrac{\cos(30^\circ)-\sin(30^\circ)}{\cos(30^\circ)+\sin(30^\circ)}$

$= \dfrac{ \frac{1}{2}\sqrt{3} - \frac{1}{2} } { \frac{1}{2}\sqrt{3} + \frac{1}{2} }= \dfrac{ \sqrt{3} - 1 } { \sqrt{3} + 1 }= \dfrac{ (\sqrt{3} - 1)^2 } { (\sqrt{3} + 1)(\sqrt{3} - 1) }= \dfrac{ 4 - 2\sqrt{3} } { 2 }= 2 - \sqrt{3}$

So the total area of both green triangles is $2 \times \frac{1}{2} \cdot 1 \cdot (2 - \sqrt{3}) = 2 - \sqrt{3}$ .

And the area of the blue triangle is also $\frac{1}{2} \cdot (1 - (2 - \sqrt{3}))^2 = \frac{1}{2} \cdot (\sqrt{3} - 1)^2 = \frac{1}{2} \cdot (4 - 2\sqrt{3}) = 2 - \sqrt{3}$ .

Conclusion: The total area of both green triangles is equal to the area of the blue triangle.

Let $s$ be the side length of the square ABCD and $x$ be the side length of the equilateral triangle AEF, as shown below.

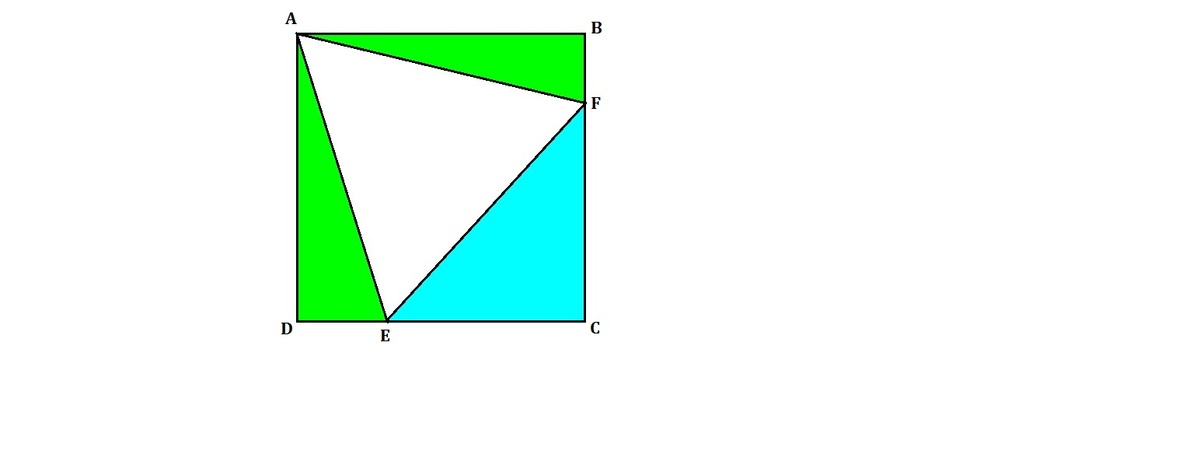
Since the triangles ADE & ABF have the equal 2 sides (AB=AD; AE=AF) and are both right-angled, they are congruent, and so the triangle EFC is an isoscales triangle because the angles $\angle FEC$ & $\angle EFC$ are also equal.

Then $EF^2$ = $EC^2$ + $FC^2$ = 2 $EC^2$ = $x^2$ . Thus, $EC = \frac{x}{\sqrt 2}$ .

Then $DE = BF = s - (\frac{x}{√2}$ ), and $AE^2$ = $AD^2$ + $DE^2$ .

Hence, $x^2$ = $s^2$ + $[s - (\frac{x}{\sqrt 2})]^2$

0 = 2 $s^2 - sx\sqrt{2} - \frac{x^2}{2}$

Solve for $s$ in terms of $x$ , we will get: $s = \frac{x}{4}$ ( $\sqrt 2$ + $\sqrt 6)$ .

Therefore, the area of the square ABCD = $s^2$ = $\frac{x^2}{16}$ (2 + 4 $\sqrt 3$ + 6) = $\frac{x^2}{2}$ + $\frac{x^2(\sqrt 3)}{4}$

By using the formula, we known that the area of an equilateral triangle with side length x = $\frac{x^2(\sqrt 3)}{4}$ .

That means, when we subtract the triangle area from the square, the rest of the areas (sum of blue & green lands) = $\frac{x^2}{2}$ .

We can then calculate the area of the blue land = $\frac{1}{2}$ $EC^2$ = $\frac{x^2}{4}$ .

Then the area of the green land = $\frac{x^2}{2}$ - $\frac{x^2}{4}$ = $\frac{x^2}{4}$ .

As a result, the green & blue regions have the same amount of area = $\frac{x^2}{4}$ .

Simpler than the rest, such equilateral triangle in a square , will always divide it into 3 portions, with 2 equal to one's area

I didn't even use maths for this one, I simply imagined one side of the triangle flat against, and completely parallel to, one side of the square. Assuming of course the square is perfect and the triangle is perfectly equilateral, as you change the orientation of the triangle, the ratio of Green:Blue area never changes, because as one decreases the other increases at the same rate. Easy.