What a chain! 4
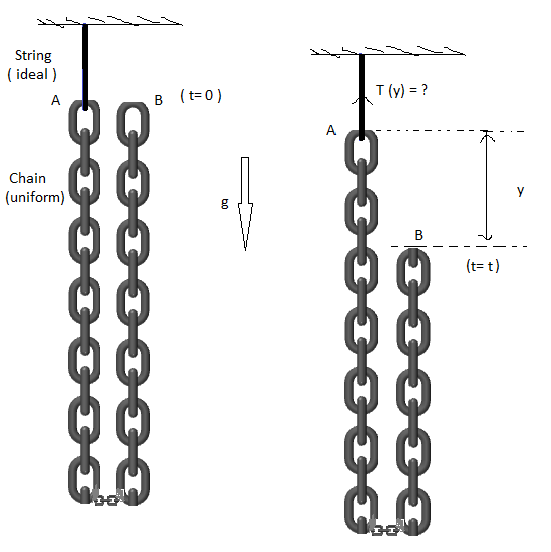
A chain of uniform mass density and mass and length is hanging from ceiling through a string. The other end of the chain is held at rest at the position shown in the figure. At time the held part of chain is left to fall under gravity. Find the tension in the string as a function of time (neglecting friction). Your answer can be represented as
where , , and are positive coprime integers. Enter your answer as .
Note : Figures are not to scale.
This is inspired by Depanshu's Chain please don't fall! and is a part of my set Aniket's Mechanics Challenges .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First of all lets find out the Tension as a function of distance falled(y) or T ( y ) .
So We can see that 2 L + y λ = m , where m=mass of the left portion.
d t d m = 2 λ d t d y
⟹ F t h r u s t = 2 λ v and v = 2 g y .
Now the force due to the mass of the rope,
F w e i g h t = T − m g .
Also F w e i g h t − F t h r u s t = m a ....
Hence F w e i g h t − F t h r u s t = m × 0 as there is no accleration of the left chain.
F w e i g h t = F t h r u s t ⟹ F w e i g h t = 2 λ v = λ g y
So putting in the equation with Tension we get
T ( y ) = 2 λ g ( L + 3 y )
Now we know v 2 = 2 g y and v = g t
So y = t 2 g
Again T ( t ) = 2 λ g ( L + 3 t 2 g ) ⟹ 2 M g + 4 L 3 M g 2 t 2
So a + b + c = 2 + 3 + 4 = 9