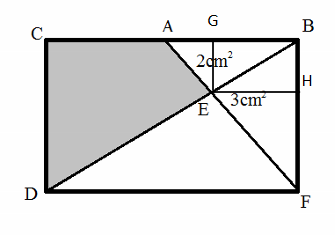
Rectangle Divisions
 B
C
D
F
is a rectangle. Triangle
A
B
E
has an area of
2
cm
2
. Triangle
B
E
F
has an area of
3
cm
2
.
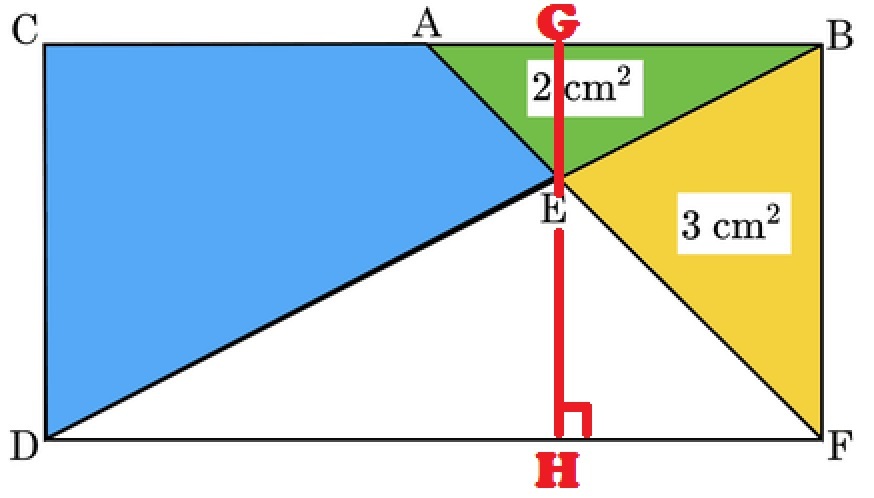
B
C
D
F
is a rectangle. Triangle
A
B
E
has an area of
2
cm
2
. Triangle
B
E
F
has an area of
3
cm
2
.
Find the area of the blue region (in cm 2 ). Give your answer to 1 decimal place. (The figure is not drawn to scale. )
Note: This question is supposed to be harder than it looks like. Do not assume anything that is not stated in the problem! (Hint: Angle E is NOT 90 degrees, nor is A the midpoint of BC.)
The answer is 5.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Nice Problem @Margaret Zheng ... :D
Log in to reply
thanks I will post some more
Nice problem with nice solution .
if A is the mid point of CB then the shaded area will b 8 square centimeter
Log in to reply
But A wasn't given to be the midpoint, and considering the given values, cannot be the midpoint.
Log in to reply
That was a mistake I also made, and was wondering about the numbers...
Triangles ABE and DEF are similar, with linear ratio 2:3. Therefore AB is 2/3 of DF. Therefore AB is 2/3 of CB. Therefore A is 1/3 of the way along CB.
This problem works with rectangles of different proportions (e.g. square or long & thin), but A has to be one third of the way along the side, if the green and yellow areas are 2 and 3.
why are angle aeb and feb 90.?? why are we assuming that???
Log in to reply
nop they are not 90
Log in to reply
If ABE and DEF share the same height then line-BE should be perpendicular to line-AF. This is not given in the problem.
Log in to reply
@Ian Iran – The line-BE is not the height being referred to in this topic. It is correct that the height of a triangle is always perpendicular from its base to the opposite vertex. The height of triangles ABE and BEF being mentioned here is the height of the triangle ABF with line-AF as its base. It is the line perpendicular to line-AF extending to vertex B. Hope it helps.
a questionable question.....actually....
No, I never said that the shared height was B E . I never assumed that anywhere, if you look carefully.
Don't ABE and EBF share a height? On line 2, you said it was ABE and DEF.
Log in to reply
Oh, thanks for pointing that out! I'll fix it. :D
Nice one.... R@j
"Note that ABE and DEF are similar."
Can you explain this part to me? I thought in order for them to be similar the bisector should be perpendicular to point B and create two 90 degree angles?
Log in to reply
I would try to explain how I prove this (yes, my proofs are probably not the ones on your textbook) draw an auxiliary line that goes through point E and is perpendicular to segment AB. Then you have divided ABE and DEF both into smaller triangles. Now for both pairs of triangles, you have the vertical angle and the right angle to prove that the pair of small triangles are similar; therefore, all three of their sides are proportional. Do you get what I am trying to say? If not, I will try to make it clear.
Log in to reply
Got it thanks. I seem to have tangled up my right triangle properties. I thought it said "BEF" instead of "DEF" hence why I was looking for the 90 degrees.
I was also gonna ask about why (AE/EF)^2 is equal to the ratio of two triangles, then I remembered that they're basically just halved squares. I'm super rusty, but interesting nonetheless. Thanks for coming to my rescue, I would've saved this problem and asked my friends simply because I thought D was B.
Log in to reply
@Jan Edmark Arieta – Thanks for the compliment and I'm glad that you got it!
The last line above appears to be EACD + triangleABE = EACD which is evidently incorrect???
Log in to reply
Oh, that's actually a long right arrow for implication. Possibly looks like an equal to sign. I'll edit it to the next line.
I entered 11/30 because it's 11/30 of the area of the whole rectangle. Correct as far as it goes, but one must remember the 2 and the 3.
Why do you say the two triangles share a height? That would only be true if AF and DB are perpendicular, which not only wasn't stated but doesn't even look like they are in the diagram.
Log in to reply
You are right that AF and DB aren't perpendicular. But, the height we're interested doesn't have anything to do with them.
If you consider the base of triangle ABE to be AE, then its height is the length of some line you draw from B that's perpendicular to AF. Note that this new line is not the same as BE.
Similarly, if you consider the base of triangle BEF to be EF, then its height is the length of some line you draw from B that's perpendicular to AF, the same line you drew as the height for triangle ABE.
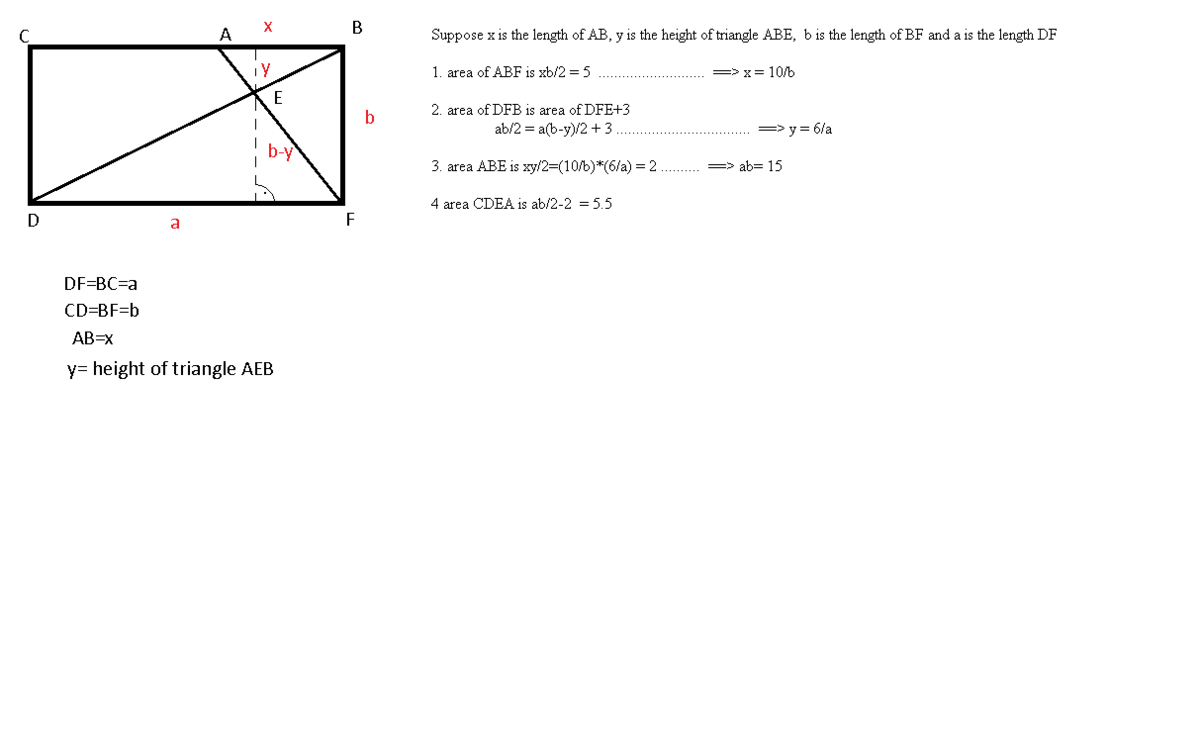
Let EG be the height of △ABE and EH be that of △BEH.
Suppose x is the length of AB. The area of △ABF= 5 = ½ x BF.
So BF is 10/x. Then the area of △BEF= 3 = ½ (10/x) EH; EH= 3x/5.
Likewise, the area of △ABE= 2 = ½ x GE; GE = 4/x.
The rectangle BGEH has one vertex on the diagonal of the big rectangle, so they are similar.
So GE:EH = BF:DF.
Since BF:BH = BF:GE = (10/x)/(4/x) =2.5,
DF = 2.5(EH) = (2.5)(3x/5) = 1.5x.
Thus, the area of rectangle BCDF = 1.5x*10/x = 15.
The area of △DEF = ½ DF HF = ½ 1.5x 6/x =4.5.
As a result, the shaded area = 15-4.5-2-3 = 5.5 cm2.
that was what I thought to be the answer, but u guys gave me more inspirations! thanks!
impecable!
Thanks. never though in this way!
Interesting, you solved it using similar rectangles, rather than similar triangles (which is the course topic)
△ s A B E a n d F B E h a s b a s e A E a n d F E b u t s a m e h e i g h t . ∴ F E A E = 3 2 . . . . . . . △ s A B E a n d F D E a r e s i m i l a r . ∴ A r e a F D E A r e a A B E = ( 3 2 ) 2 = 9 4 ∴ A r e a F D E = 4 . 5 . ⟹ A r e a B D F = 4 . 5 + 3 = A r e a B D C = A r e a A E D C + A r e a A E B ∴ A r e a A E D C = 4 . 5 + 3 − 2 = 5 . 5
why are u considering angle AEB and FEB 90 degree?
Log in to reply
No, I have not. I said the triangles have the same height.
in third line which theorm is applied?
Log in to reply
That is just a result when the area of two congruent figures is compared. If two polygons are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides. For more: http://regentsprep.org/regents/math/geometry/gp11/lmoresimilar.htm
Proper LaTeX code would say \triangle\text{s }ABE\text{ and }FDE\text{ are similar}. And \left( \frac 2 3 \right) so that the parentheses will have appropriate sizes. Writing \operatorname{Area} will de-italicize that word and proved proper spacing, and how much is proper depends on whether you write \operatorname{Area}(ABC) with parentheses (then there's only a thin space) or \operatorname{Area}ABC, in which case a space comparable to that between words of text appears.
Nice way to solve this question sir.
- area ABE is xy/2=(10/b)*(6/a)/2=2.......ab=15 (typo) thanks, very clear
Interesting that we can introduce so many unknowns and still solve it!
Rotate the rectangle 180 degrees and let B=(0,0), E=(x,y), A=(l,0), D=(b,h). We have l y = 4 h x = 6 l h = 1 0 y / x = h / b ⟹ ( l h ) ∗ ( h x ) / ( l y ) = 1 5 ( h 2 ) ( x / y ) = 1 5 ( h 2 ) ( b / h ) = 1 5 b h = 1 5 △ B C D = b h / 2 − 2 = 5 . 5
Please: Write \cdot or \times for multiplication. An asterisk is a workaround for occasions when you are limited to the characters on the keyboard.
 (FBAB)/2 = area = 2 cm^2 + 3 cm^2 = 5 cm^2; FBAB = 10 cm^2; AB = 10/FB; AB^2 + FB ^2 = AF^2; (10/FB)^2 + FB^2 = AF^2; 100/FB^2 + FB^2 = AF^2; FB^4 – AF^2FB^2 + 100 = 0; (FB^2 – 10)^2 = 0; FB^2 = 10
FB = sqrt(10); -AF^2FB^2 = -20FB^2, so AF^2 = 20, so AF = sqrt(20) = 2*sqrt(5); Since AB^2 + FB^2 = AF^2, we get AB^2 + 10 = 20. Thus, AB^2 = 10, and AB = sqrt(10) = FB.
(FBAB)/2 = area = 2 cm^2 + 3 cm^2 = 5 cm^2; FBAB = 10 cm^2; AB = 10/FB; AB^2 + FB ^2 = AF^2; (10/FB)^2 + FB^2 = AF^2; 100/FB^2 + FB^2 = AF^2; FB^4 – AF^2FB^2 + 100 = 0; (FB^2 – 10)^2 = 0; FB^2 = 10
FB = sqrt(10); -AF^2FB^2 = -20FB^2, so AF^2 = 20, so AF = sqrt(20) = 2*sqrt(5); Since AB^2 + FB^2 = AF^2, we get AB^2 + 10 = 20. Thus, AB^2 = 10, and AB = sqrt(10) = FB.
(EG * AB)/2 = 2 cm^2 = (EG * sqrt(10))/2. So EG*sqrt(10) = 4. EG = 4/sqrt(10); EH = FB – 4/sqrt(10) = sqrt(10) – 4/sqrt(10) = 10/sqrt(10) – 4/sqrt(10) = 6/sqrt(10);
Triangle AEB is similar to triangle DEF, so EG/EH = AB/DF = 4/sqrt(10) / 6/sqrt(10) = 4/6 = 2/3; AB/DF = 2/3 = sqrt(10)/DF. 2DF = 3sqrt(10). DF = 3sqrt(10)/2; Area of triangle DBF = (EHDF)/2 = (6/sqrt(10) times 3sqrt(10)/2)/2 = (18/2)/2 = 4.5.
So area of triangle BCD = 4.5+3 = 7.5. That means the blue area is 7.5-2 = 5.5.
Triangles \triangle\text ABE and ABF have the same base, so the ratio of their areas (2/(2+3)) = the ratio of their heights. When you go on the diagonal from B to D, by the height you reach E, you have descended 2/5 of the height of the rectangle (BCDF does not need to be a rectangle, it is enough to say it is a parallelogram, we get the same result!), thus BE is the 2/5 of BD. Enlarge triangle ABE keeping B: E goes to D, A goes to A'. Triangle A'CD is congruent to ABF, their area is 5 cm2. The enlarged sides and heights of A'BD are 5/2 times of those of ABE, thus the area of A'BD=5/2 * 5/2 *2 =12.5, of which 5 is A'CD, 2 is ABE, thus 5.5 cm2 is the blue area.
It is clear that,
[FBA] = [DBA]
hence,
[DEA] = 3
From the given areas, we have
[ABE] : [BEF] = AE : EF
also,
[DEA] : [DEF] = AE : BF
It implies
[ABE] : [BEF] = [DEA] : [DEF]
So
3 : [DEF] = 2 : 3
then we get
[DEF] = 4.5
Finally
[DEF] + [BEF] = [ACDE] + [AEB]
4.5 + 3 = [ACDE] + 2
from this,
[ACDE] = 5.5
You say that 2x = 3. I don't understand why. And what is x?
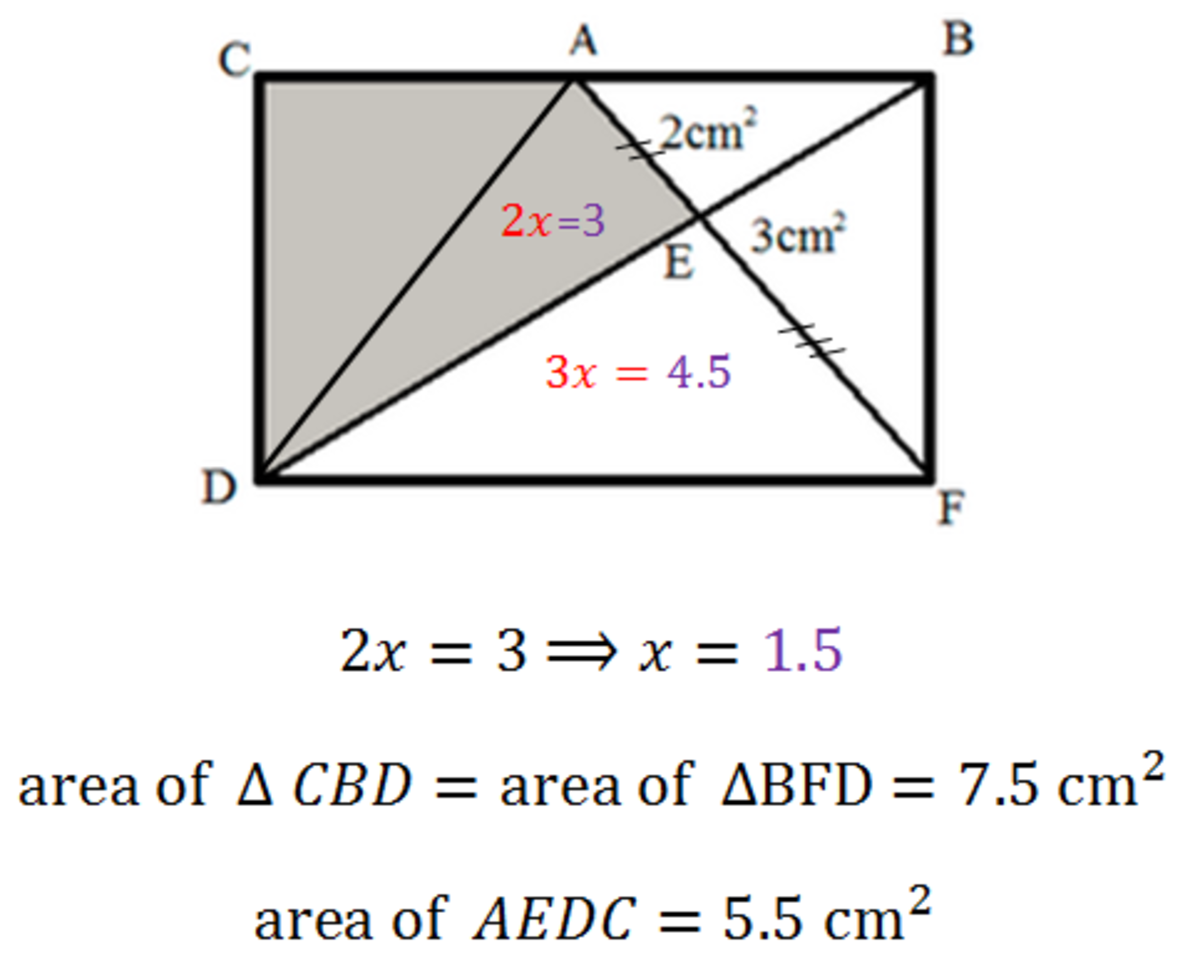
Δ D E F Δ A B E = ( E F A E ) 2
Since Δ A B E = 2 c m 2 ,
Δ D E F = ( 2 3 ) 2 × 2 = 4 . 5 c m 2
Δ D E F + Δ B E F = E A C D + Δ A B E
⟹ E A C D = 5 . 5 c m 2