What a game!

Assuming they keep tossing even after the game has been won, Anik and Nihar's tosses form an infinite sequence of heads and tails. We want the probability that the first head occurs in an even position. This can be found by summing an infinite series of independent probabilities...

P(first head in position 2) + P(first head in position 4) + P(first head in position 6) + ...

$=\left(\frac{1}{2}\times\frac{1}{2} \right)+\left(\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\right) +\left(\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}\right)+ \dots$

This is a geometric series with first term and common ratio both $\frac{1}{4}$ which sums to

$\dfrac{\frac{1}{4}}{1-\frac{1}{4}}=\boxed{\frac{1}{3}}$

Let the probability that Anik wins be $P.$ If Anik throws a tail on his first toss, (which has a probability of $\frac{1}{2}$ of occurring), then we can essentially "restart" the game with Nihar being the player with the "first" toss, i.e., Nihar takes the place of Anik in this restarted game. Thus the probability that Nihar wins the (original) game will be $\frac{1}{2}P.$

Since the probability that either Anik or Nihar will (eventually) win is $1,$ we have that

$P + \dfrac{1}{2}P = 1 \Longrightarrow \dfrac{3}{2}P = 1 \Longrightarrow P = \dfrac{2}{3},$

and thus the probability that Nihar wins is $\dfrac{1}{2}P = \dfrac{1}{3}.$

Thus $\alpha + \beta = 1 + 3 = \boxed{4}.$

Comment: Technically the game could go on forever, but from a probability standpoint this "event" occurs with zero probability, leading to my statement that the probability that one of the players will eventually win is $1.$

M:Me

N:Nihar

Possible combinations : (MN, MNMN, MNMNMN... till infinity) for Nihar winning the game.

Therefore total Probability = P(MN) + P(MN)*P(MN) + P(MN)^3 ... till infinity. This forms a GP.

Therefore Probabilty = P(MN)/(1-P(MN)) <- Formula for infinite GP = (0.5 x 0.5)/(1-0.5 x 0.5) = 1/3

I typed a COMPLETLEY random number and got it right the first try, That is how I got my solution

Take P(I) as I win and P(N) as Nihar wins. Now if I flip the coin once, either I win or Nihar gets a go to win. P(I)=0.5+0.5 P(N), 1-P(N)=0.5+0.5 P(N), P(N)=1/3

Say x is the probability I win. I play first, and win pith p= $\frac{1}{2}$ The other option is that p= $\frac{1}{2}$ Nihar plays. He either wins $p= \frac{1}{2} \cdot \frac{1}{2}$ and he wins, or I have another chance to win with probability again x (since the game is exactly as initially) Therefore $x= \frac{1}{2} + \frac{1}{4} \cdot x$ So $x= \frac{2}{3}$ So Nihar wins with $p_{Nihar}= \frac{1}{3}$

I just guessed and got it write omg

Let p be the probability for Nihar to win.

The probability that Anik does not win directly at the start by tossing a head is 0.5, so in case Nihar tosses a head (probability 0.5 * 0.5 = 0.25), he wins. In case they both toss tails (probability 0.5 * 0.5 = 0.25), the game is essentially restarted. Thus

p = 0.25 + 0.25 * p

and therefore

p = 1/3

holds.

• Since alpha and beta are both coprime numbers. alpha = 1, beta = 3. 1+3 = 4. the solution to 1 + 3 = 4

Alternative solution: You can draw a tree of the possibilities; when [H]ead, stop; when [T]ail, branch again. The [H] in every second "layer" is good for Nihar, framed in the picture below:

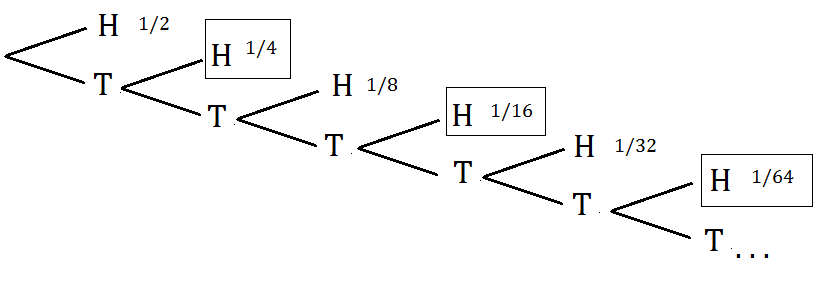
If you sum the probabilities for Nihar, you get $\mathbb{P}($ Nihar wins $) = \frac12 + \frac18 + \frac1{32} + \frac4{128} + \dots$

the same for your case is $\mathbb{P}($ You win $) \frac14 + \frac1{16} + \frac1{64} + \frac1{256} + \dots$

The ratio of the two probabilities is $\frac{ \mathbb{P}(Nihar) }{ \mathbb{P}(You) } = \frac{ \frac14 + \frac1{16} + \frac1{64} + \frac1{256} + \dots }{ \frac12 + \frac18 + \frac1{32} + \frac4{128} + \dots } = \frac12$ , since the $n$ th element of the top sum is always half of the corresponding element of the bottom sum.

Since one of you has to win, $\mathbb{P}(Nihar) + \mathbb{P}(You) = 1$ , which can only happen if $\mathbb{P}(Nihar) = \frac13$

If Nihar wins then the first toss must be tails. Then if he got heads, he would win. There is a 1/4 chance that could happen. However, if he also got a tail, and then I got a tail (remember we are focusing on him winning), and then he gets a head, that would be a probability of 1/16. This keeps on repeating.

So the probability 1/4 + 1/16 + 1/64 + 1/256... We need to evaluate this sequence.

Let S = 1/4 + 1/16 + 1/64 + 1/256... 4S = 1 + 1/4 + 1/16 + 1/64...

4S = S + 1 3S = 1 S = 1/3

The probability of getting a first head in the $n$ th toss is $(1/2)^n$ .

I win if $n$ iss odd. So, the probability of me winning is $M = 1/2 + 1/8 + 1/32 + ...$

Nihar wins if $n$ iss even. So, the probability of Nihar winning is $N = 1/4 + 1/16 + 1/64 + ... = (1/2)*(1/2 + 1/8 + 1/32 + ... ) = M/2$ .

The sum of probabilities is $1$ (either i win or Nihar wins). So, $1 = M + N = M + M/2 = 3M/2$ . Then, $M = 2/3$ and $N = 1/3$ .

The answer is $4$ .