What about the aspect ratio?
When you try to buy a (rectangular) TV in a shopping mall, you will find that the size of a TV screen is described by the length of its diagonal in inches.
If the size of a certain TV screen is 34 inches, and the other two dimensions (length and width) are also integers (in inches), what is the perimeter of this TV screen in inches?
Clarification: The perimeter is 2-dimensional, not including the thickness of the TV screen.
The answer is 92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It can be easily observed that
3 4 2 = 3 0 2 + 1 6 2 .
so the perimeter comes out to be 2 ( 3 0 + 1 6 ) = 9 2
Is the answer unique?
How do you know that is the only ratio? You need to prove this, using Pythagorean Theorem.
Log in to reply
Quadratic residues ? Really? Don't we just need to find all the primitive Pythagorean triples with hypotenuse 17? Or in other words, find all pairs of positive integer solutions to m 2 + n 2 = 1 7 ?
Log in to reply
Haha! Thought that might be an approach. Seems like there is no easy start. It's easy to realize that Pythagorean triple is of course 8 − 1 5 − 1 7 , but I expect an interesting mathematical proof. :)
Oh well. :)
Log in to reply
@Michael Huang – Depends on how much power you want to use. In this case, since it's a level 1/2 problem, I would recommend just stating trial and error.
More generally, we can use the sum of squares classification.
34²=x²+y² Formula for Pythagorean triples z=k(m²+n²)=34,m>n, x=k(m²-n²), y=2kmn So for k=1, m=5,n=3 So x=16, y=30 or For k=2, m=4,n=1, x=30, y=16 So solution is 2(x+y)=92cm
If the tv size gets really big, we can factor the size and then find a sum of squares for a smaller number.
34 = 17x2 = 2(4^2 + 1^2) = k(m^2+n^2)
a=2(4^2-1^2)=30 = k(m^2-n^2)
b=2x2x4x1=16 = 2kmn
P=2(16+30)=92
In this case, theres not much difference between finding a sum of squares that gives us 34...(25+9) and other that gives us 17...(16+1) but maybe you can find factoring useful if you can't notice any sum of squares that add up.
The TV above is rectanglular, which means we can cut it into two congruent triangles along its diagonal. By doing this we have a 30-60-90 triangle. a 30-60-90 has the following angles and side lengths:
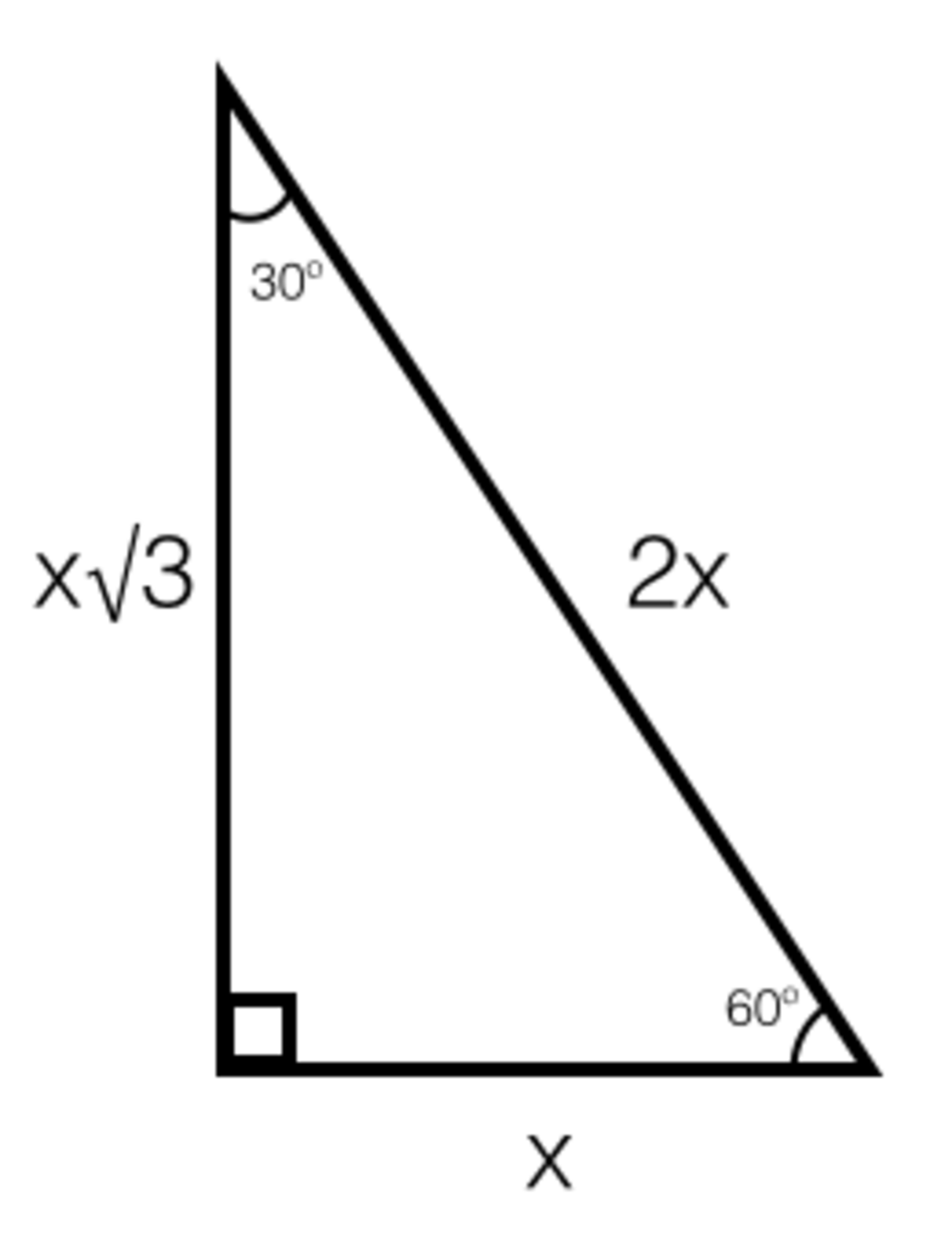
We can solve this problem using what we know about special right triangles. First of all, we have our hypotenuse, which is 34". Since the hypotenuse of any 30-60-90 triangle is equal to one of the legs doubled, we will then find x, which is 17". Now that we have x, we can find our other side length, which is equal to 17√3, or 29.4448637..., which we round to be 29". We then add 17+29+17+29 to get 92".
No, this is incorrect. You can't round up the side lengths.
Note that I stated that the sides are integers, so one of the side lengths cannot be 17√3.
Log in to reply
But I rounded it to an integer in my solution.
Log in to reply
Doesn't matter. I stated that the side lengths are integers, I didn't state that "the side lengths are non-integers that round up to an integer".
Log in to reply
@Pi Han Goh – I'm sorry, I feel like an idiot!
Log in to reply
@Deva Craig – Don't worry, everyone makes mistakes. Keep trying and you will get eventually get the hang of it! ;)
Log in to reply
@Pi Han Goh – Sorry about that, I don't particularly think highly of myself at times.
Log in to reply
@Deva Craig – Haha you got to stop apologizing, nobody's mad at you. We're all here to learn~
Log in to reply
@Pi Han Goh – OK! :) I enjoyed your problem, and the way you explained your solution did get me to see integers and decimals in a new way!
Log in to reply
@Deva Craig – No problem. By looking at the other solution (and their respective solution discussion), you should probably already know that we need to apply Pythagorean theorem ...
Message me (here) if you need any help~~
Log in to reply
@Pi Han Goh – How exactly do you find the other Pythagorean triples if they are in fact integers?
Log in to reply
@Deva Craig – Well, first notice that if ( a , b , c ) is a pythagorean triplet , then so is ( k a , k b , k c ) , where k is any positive integer.
For example, we know that ( 3 , 4 , 5 ) is a Pythagorean triplet, so ( 6 , 8 , 1 0 ) and ( 9 , 1 2 , 1 5 ) are also Pythagorean triples.
Now we call a Pythagorean triplet as primitive if the greatest common divisor of a , b , c is 1. For example, 3 , 4 , 5 does not share any common divisor larger than 1, so ( 3 , 4 , 5 ) is a primitive Pythagorean triplet, whereas 6 , 8 , 1 0 share a common divisor of 2, so ( 6 , 8 , 1 0 ) is not a primitive Pythagorean triplet.
Now back to this question. We want to find all the integers ( a , b , 3 4 ) such that ( a , b , 3 4 ) is a Pythagorean Triplet, and that a , b are less than 34.
Consider two cases: What if ( a , b , 3 4 ) is a primitive Pythagorean triplet? And what if ( a , b , 3 4 ) is not a primitive Pythagorean triplet?
Do you know how to proceed?
Log in to reply
@Pi Han Goh – Wait, I think I got a simpler explanation.
Note that all Pythagorean triplets ( a , b , c ) are in the form ( m 2 − n 2 , 2 m n , m 2 + n 2 ) , where c is the largest value among the 3 numbers ( a , b , c ) , and m , n are positive integers with m > n .
In this question, c = 3 4 , so c = 3 4 = m 2 + n 2 . Now, we just need to find the integers m , n that satisfy this condition. The values are m = 5 , n = 3 only. So the other two integer side lengths are m 2 − n 2 = 5 2 − 3 2 = 1 6 and 2 m n = 2 × 5 × 3 = 3 0 .
So the perimeter of this rectangle is just 2 × ( 3 4 + 3 0 ) = 9 2 .
@Pi Han Goh – I didn't exactly think of rounded integers and just plain or regular integers as different things.
Formula for pythagorean triplets is z=k(m²+n²),x=k(m²-n²),y=2kmn. m,n,k are positive integers,m>n. z=34,so k=1 or 2 (17 and 34 can't). For k=2. m²+n²=17, so m=4,n=1. Then x=2(4²-1)²=30, y=16 Similiar for k=1, we'll get x=16,y=30. So answer is 2(16+30)=92cm