What do you call a shoe made from bananas?

Logic Level 4

I have 6 separate baskets none of which is contained in another. In these baskets you will find plums, apples and bananas. In each basket there are as many plums as apples in all the other baskets combined. Moreover, in each basket, there are again as many apples as bananas in all the other baskets combined.

What is the largest integers that the total number of fruits is always divisible by?

The answer is 31.

3 solutions

A Former Brilliant Member
Feb 27, 2016

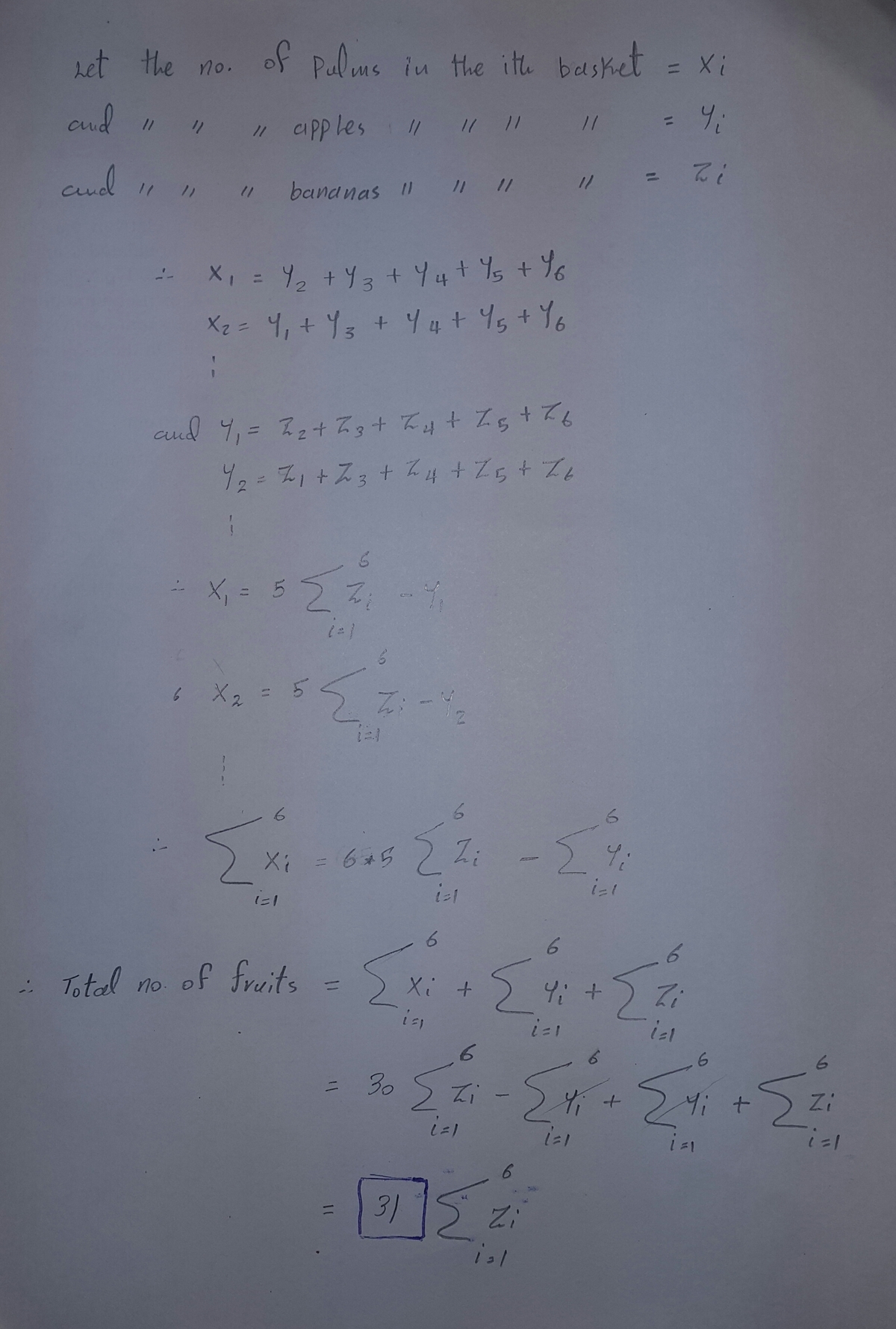
First, let's consider statement $1$ :

In each basket there are as many plums as apples in all the other baskets combined.

This tells us that the number of plums in basket $1$ is equal to the number of apples in baskets $2, 3, 4, 5, 6$ combined. Draw a table.

Plums:

Sum of:

Basket 1:

Basket 2, Basket 3, Basket 4, Basket 5, Basket 6

Basket 2:

Basket 1, Basket 3, Basket 4, Basket 5, Basket 6

Basket 3:

Basket 1, Basket 2, Basket 4, Basket 5, Basket 6

Basket 4:

Basket 1, Basket 2, Basket 3, Basket 5, Basket 6

Basket 5:

Basket 1, Basket 2, Basket 3, Basket 4, Basket 6

Basket 6:

Basket 1, Basket 2, Basket 3, Basket 4, Basket 5

Each basket containing apples appears $5$ times. Thus, the total number $p$ of plums is $5$ times that of apples, and by the same logic, the total number of apples is $5$ times that of bananas.

Therefore, the total number of fruits is $n+5n+25n=31n$ , if $n$ is the number of bananas. It is always divisible by $31$ . $_\square$

$\text {Answer to question "what do you call a shoe made from bananas?": a slipper.}$

You have calculated the number of total fruits in one basket whereas the question asks total number of fruits in all baskets combined , hence 31n×6 = 186 . So , the answer can be any divisor of 186 .

Ujjwal Mani Tripathi - 5 years, 3 months ago

Agree. Was slightly annoyed to find that neither 186 nor 6 was correct.

Will Hawkes - 5 years, 3 months ago

If there was only one banana, there would be 5 apples (1 for every other basket) and 25 plums (5+4+4+4+4+4), making a total of 31 fruits, which is not a multiple of 186.

Ferran Espuña - 5 years, 3 months ago

@Ferran Espuña – Good point.

Will Hawkes - 5 years, 3 months ago

Consider this distribution ---

30 plums, 5 apples and 2 bananas in one basket. (37 fruits)

29 plums, 6 apples, 1 banana in each of the remaining 5 baskets. (36 fruits in each basket)

It satisfies all the conditions and the total number of fruits is 217. Divisible by 31...

Satyen Nabar - 5 years, 3 months ago

Thamk you @Satyen Nabar for the explanation . I was thinking only one aspect .

Ujjwal Mani Tripathi - 5 years, 3 months ago

Nice explanation and second question!

Akhash Raja Raam - 5 years, 3 months ago

Ajinkya Shivashankar
Oct 17, 2016

Basket	1	2	3	4	5	6
Bananas	a	b	c	d	e	f
Apples	S-a	S-b	S-c	S-d	S-e	S-f
Plums	4S+a	4S+b	4S+c	4S+d	4S+e	4S+f

Where S = a+b+c+d+e+f

Total number of fruits = 31S

Abdelrahman Sabri
Apr 28, 2016

What do you call a shoe made from bananas?

The answer is 31.

3 solutions

0 pending reports