Classify this real number!
 n
=
1
∑
∞
2
n
2
1
n
=
1
∑
∞
2
n
2
1
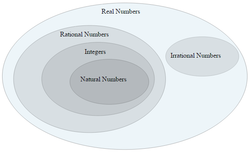
In mathematics, a real number is a value that represents a quantity along a continuous line. The real numbers include all the rational numbers, irrational numbers. And some irrational numbers are transcendental.
What kind of number is the expression above?
Image Credit: Wikimedia Real numbers by Damien Karras
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
follows link, gets intimidated, posts comment. +1
Log in to reply
Hahaha. Yeah, I found that proof pretty intimidating too. :)
The given series is not the type covered in Theorem 15. That series has a geometric progression in the powers 2^k. Not k^2.
Log in to reply
Oh darn. Thanks for catching my error. I tend to transpose terms when I'm tired and I did this problem after midnight last night, (as I recall). :P O.k. then, I'll edit my solution to indicate that the link proves the transcendence of a different number and that the proof of the transcendence of the number in this question remains elusive. n 2 grows too slowly to ensure that the number here is a Liouville number so we can't automatically conclude that the given number is transcendental. There will have to be a tailor-made proof then.
Log in to reply
Does it really grow too slowly? I'd think that by the definition of a Liouville number n 2 would grow quickly enough, making the sum a Liouville number.
Log in to reply
@Jake Lai – Oh, I left a reply above to your (now deleted) comment. So as stated there, I think it does grow too slowly. The topic of Liouville numbers is new to me so I'm trying to get a handle on it, but I'm not certain anymore if the number in this question is in fact known to be transcendental or not.
Log in to reply
@Brian Charlesworth – I posted a problem which happens to (hopefully) be a corollary of the theorem you linked, after giving the proof a quick glance. Might have to remove it, though, if the term in my sum still grows too slowly.
Log in to reply
@Jake Lai – I actually had a look at your problem just before being notified of your comment. :) I don't think this one grows fast enough either; with a n = ( n 2 n ) we would have lim n → ∞ a n a n + 1 = 4 , and we want this limit to be ∞ to be certain of transcendence. Your number may be transcendent, but until we're sure it might be better to delete it for now. Sorry. :( You could post a problem involving the Fredholm number I linked to in my solution; I'd be fine with that. :)
Log in to reply
@Brian Charlesworth – Michael mentioned an excerpt of "Introduction to Algebraic Independence Theory" in the disputes, so I consulted my old friend Uncle Google.
After a bit of digging around I found this abstract and a couple of pages (click "Look Inside") on the proof of the transcendence of numbers of the general form ϑ 3 ( z ) = ∑ z n 2 for z ∈ Q ∩ ( − 1 , 1 ) . Hope you enjoy.
Log in to reply
@Jake Lai – Wow, you're good at digging around. :) Thanks for the link. I read the two pages provided and I'm still wondering if they definitively state the transcendence of these numbers. I think they do, but the reference to "transcendence degree over Q" has me a bit confused. But Michael's reference seems to indicate that these numbers are transcendent, so between this and your assurance I think that the matter is closed. I don't know how the asker expected us to figure all this out ourselves, as this result is quite recent and very difficult to determine.
The numbers dealt with in this paper don't appear to help with the number in the question you've posted, so I'm still trying to decide which answer option to choose. :)
@Brian Charlesworth – What's the point in asking this question if the answer is absurd
It's a difficult task to prove the transcendence of a number, but I have found a proof here . Scroll down to Theorem 15.
EDIT: The theorem I've linked to actually proves the transcendence of the Fredholm number n = 0 ∑ ∞ 2 2 n 1 and not the number in this question. (I have a tendency to transpose terms when I'm tired. Sorry. :( ) I'll have another look for the "right" proof, if in fact there is one. (This number is not on any list of transcendental numbers that I have managed to track down.)