What is that figure?
Find the area of the figure given by the Cartesian equation below:
1 6 ( x + y ) 2 + 9 ( x − y ) 2 = 1
By the way, to make the problem easier, here is a graph of the figure to help you:
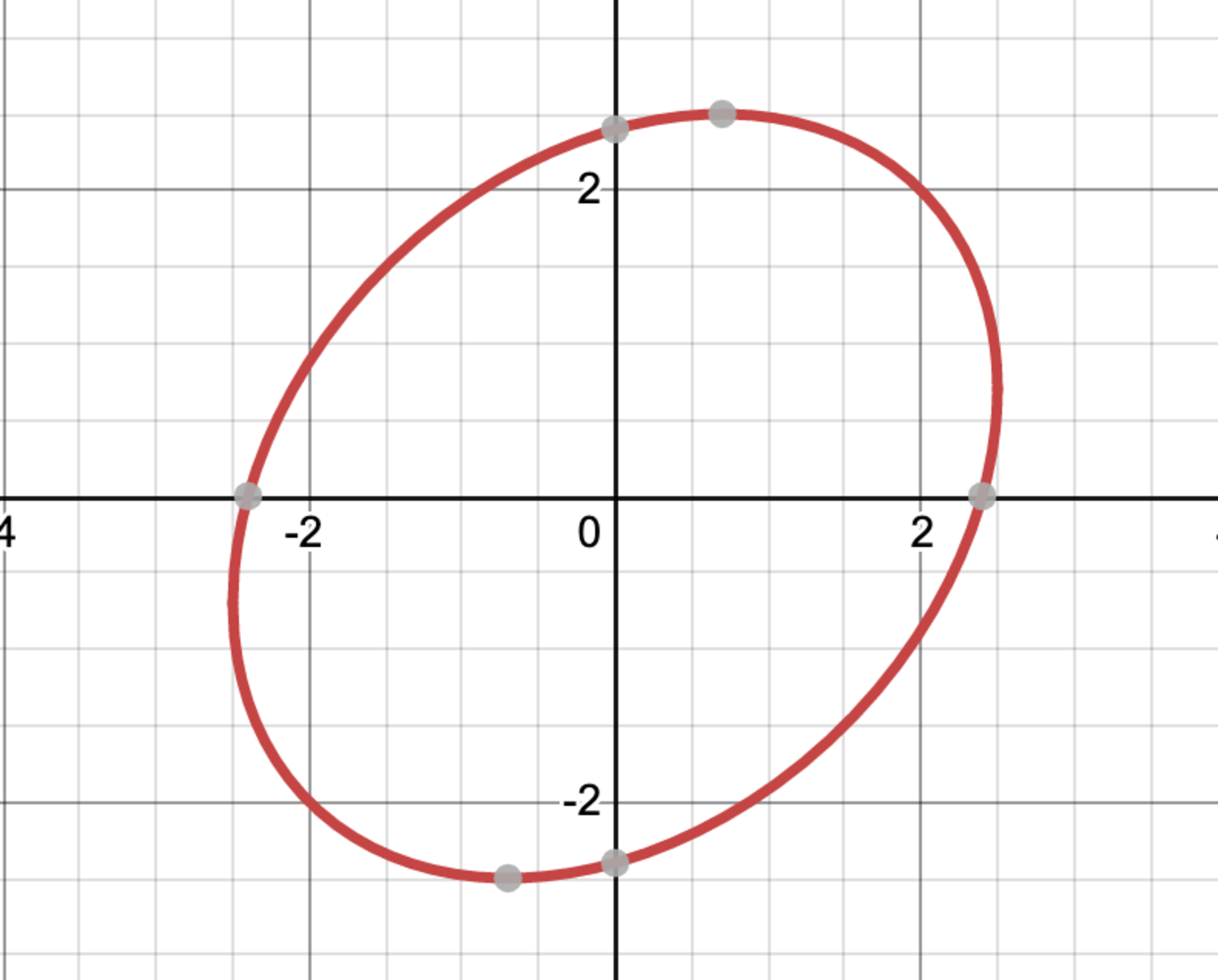
This isn't an original problem. It's a JEE problem sent to me by Lil Doug (Neeraj Anand Badgujar)
The answer is 18.85.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
@Steven Chase
(upvoted)sir is the last equation like this
A
=
2
1
×
R
×
R
d
θ
Taken from the formula of triangle. Am I correct ?
Log in to reply
Yeah, that's a pretty good way to think of it. Another way is to use the cross product formula for the area of a triangle. If two sides of the triangle are given by vectors A and B , the area is:
A r e a = 2 1 ∣ A ∣ ∣ B ∣ sin θ
In the above, θ is the angle between the vectors. So in this case, the two vectors are separated by an infinitesimal angle d θ , and the radii are approximately equal to r , and we can use the small angle approximation for sine, resulting in:
d A = 2 1 r 2 d θ
Log in to reply
Noice. I'm fascinated with using cross product/determinant to find the area.
Hmm, I like it. Evaluating in polar coordinates.
@Steven Chase
I've posted a new problem, if you want to check it out. Simulating Dynamics 5.0
Please let me know if the solution's right.
Log in to reply
@Krishna Karthik by the way how much you scored and did you have any doubt?
Log in to reply
The problems are too hard for me lol. I am not experienced enough in momentum formulation. I'm fine in Newton's Laws, and just started with momentum.
I think I got 6/24 XD
Btw 16/24 is genius level.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
I want to do that test with Steven sir.
I am just curious to know his score.
I think he will deny us for that.
What do you think?
Log in to reply
@Talulah Riley – Well, don't think too much if he scores lower than you, but he probably hasn't done timed competitive exams in 20 years lmao.
Just bear in mind that if you give it to anybody, even Stephen Hawking, they probably wouldn't get more than 10/24.
That doesn't mean that without practice they won't get as much.
However, the thing about Steven Chase is that he is exceptional at problem solving, even with only pencil-paper. He could probably get 20/24. Knowing his level of thinking, I would bet on it.
@Krishna Karthik
–
@Krishna Karthik
Bro I am allowing you to use any type computation like python/Matlab.
Then what do you think what will be your score.?
Log in to reply
@Talulah Riley – Probably wouldn't be any different. I am not familiar with the momentum model; I'm mostly just familiar with Newtonian dynamics, Conservation of Energy, and Lagrangian Dynamics.
I haven't done collision and momentum problems before.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
You have not done Rotation, Collision, Momentum.
These topics are the backbone of mechanics. .
Log in to reply
@Talulah Riley – I'm ok with Rigid Body dynamics. Just not confident with momentum and collisions. I have understood the concepts; just that I can't do super hard problems involving them.
Overall, I'm super confident in Newton's laws and Lagrangian dynamics.
I will first have a read about momentum and impulse, and then post discussions addressing doubt.
Log in to reply
@Krishna Karthik – @Krishna Karthik By the way, the teacher who has taken the test is also not able to solve some questions of the paper. Ha ha ha.
Log in to reply
@Talulah Riley – Yeah; that paper's super hard. I bet if you gave it to professors at MIT many would not pass.
Log in to reply
@Krishna Karthik – @Krishna Karthik let's give it to Steven sir.
Log in to reply
@Talulah Riley – Sure. We'll post the problems one by one. Give him a condition: no numerical methods!
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
Exactly that is what I am also thinking.
By the way bro , I am planning you to give a test of Newtonian Dynamics. I am selecting some good problems. Be ready for that.
Let u = 2 1 ( x + y ) and v = 2 1 ( x − y ) . This transformation is a rotation through 4 5 ∘ , and doesn't affect the area of the figure.
In the new coordinate system, the equation is 8 u 2 + 9 2 v 2 = 1
This is the equation of an ellipse centred at the origin with semi-major axis 8 and semi-minor axis 2 3 .
Its area is just π × 8 × 2 3 = 6 π .
@Chris Lewis
But sir how did you make it as a new coordinate system. Can you describe little more?
Thanks in advance.
Log in to reply
Let's say you have a point P ( a , b ) and you want to apply a rotation through an angle of θ anticlockwise to it, around the origin O , to get to a new point P ′ ( a ′ , b ′ ) .
It's easier to think about rotations in polar coordinates, so let's say that the distance O P = r , and the angle the line O P makes with the positive x − axis is α .
By Pythagoras, r = a 2 + b 2 .
Also, cos α = r a and sin α = r b .
Now, O P ′ will still be r (rotation doesn't change this); but the angle O P ′ makes with the positive x − axis will be α + θ .
Using trig, this gives a ′ = r cos ( α + θ ) and b ′ = r sin ( α + θ ) .
Finally, using addition formulae, we get a ′ b ′ = r cos α ⋅ cos θ − r sin α ⋅ sin θ = a cos θ − b sin θ = r sin α ⋅ cos θ + r cos α ⋅ sin θ = a sin θ + b cos θ
This is a general formula for rotation about the origin in 2D.
If you plug θ = − 4 5 ∘ into this, you get the transformation I used to get to ( u , v ) .
Hope that makes sense - it's much easier with matrices/complex numbers, but this is a purely geometric approach.
Lastly, the way to spot that a 4 5 ∘ rotation might be helpful is when you see a function of x − y and x + y .
Log in to reply
@Chris Lewis
Thank you so much.
By the way can we do this with matrices/complex numbers as you said above .?
Log in to reply
@Talulah Riley – I just meant the transformation is more "natural" in those settings. That felt like a clunky explanation for how you get a rotation in coordinates.
Let x + y = 4 cos α , x − y = 3 sin α
Then
x = 2 4 cos α + 3 sin α
⟹ d x = 2 3 cos α − 4 sin α d α
y = 2 4 cos α − 3 sin α
So, y d x = 3 − 8 2 5 sin 2 α
Hence the required area is
∫ 0 2 π ( 3 − 8 2 5 sin 2 α ) d α
= 6 π ≈ 1 8 . 8 4 9 .
Mate, I absolutely love your substitution. Genius. Well done👏🏽
@Foolish Learner you just rocked.
Looking at the graph, we can tell that the equation above is in fact that of a rotated ellipse.
Writing and simplifying the expression of the above figure, we get:
2 5 x 2 − 1 4 x y + 2 5 y 2 = 1 4 4
The equation above is in the general form of a rotated ellipse, confirming our suspicions that it is one.
Now that we know that it is a rotated ellipse, the major axis can be found using Pythagoras' theorem, or by finding the furthest point to the origin by optimising this expression:
d = x 2 + y 2
We can maximise or minimise to find the major and minor axis respectively.
Of course, the easier way is using Pythagoras' Theorem when shown the graph of the equation above.
We immediately see that the furthest points are ( 2 , 2 ) and ( − 2 , − 2 ) . The closest points are ( − 1 . 5 , 1 . 5 ) ; ( 1 . 5 , − 1 . 5 )
2 2 + 2 2 = 8
2 × 1 . 5 2 = 2 . 1 2 1
Plugging the values into the equation π a b , we get 1 8 . 8 5
@Krishna Karthik but how did you optimise it??
Log in to reply
I didn't optimise. I used a graph and first showed that the equation is a rotated ellipse, then I used Pythagoras' Theorem.
Log in to reply
@Krishna Karthik
i want a little bit elaborated solution.
What you do after
d
=
x
2
+
y
2
Log in to reply
@Talulah Riley – I didn't optimise. I used the graph to work out where the furthest and closest points were.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
my dear bro. You didn't have to use graph Or anything
You have to solve through pen and paper only.
Log in to reply
@Talulah Riley – Yeah bro; it's really hard to solve only through pen and paper. To find the furthest and closest point you would have to optimise. And optimisation is long with a complicated function.
To be honest it's really hard to solve without a graph.
@Krishna Karthik it should be − 1 4 x y ?
Log in to reply
I thought it was − 4 . I'll check.
Edit: hang on... you're right. I'm just half asleep lmao.
You're right that the equation is a rotated ellipse, but you're making an assumption that the rotation is 4 5 ∘ .
You'd need to justify that somehow; I think the easiest way is to note that the equation you get is symmetric in x and y (you can swap the variables in the equation without changing it). This means the figure is symmetric in the line y = x , which (given you know it's an ellipse) tells you that y = x is an axis of the ellipse.
Log in to reply
I didn't make any assumptions. I was given a graph as was everyone who solved the problem; the graph showed the semi-major axis at ( 2 , 2 ) and the semi-minor axis at ( − 1 . 5 , 1 . 5 )
Log in to reply
That's not shown in the diagram in the question you posted.
Log in to reply
@Chris Lewis – You can see that by looking at the subdivided lines. It's a desmos picture.
I proved that the figure was an ellipse by looking at the form of the equation when simplified. It was in the form of a rotated ellipse.
That's a good way of finding out that the rotation is 45 degrees.
Here is the solution according to my textbook
After that also I am not able to understand,
Help me to explain the solution.

I don't understand how they got it. Is there some formula? I have no idea how factorials come into this. Wtf????
Edit: The solution above assumes that it is a rotated ellipse, yet they don't even bother to clarify how they know it is one.
Log in to reply
@Krishna Karthik anyone can come into anger if they see such small solution. :)
Log in to reply
I agree. It's stupidly unjustified; do they expect us to understand a solution with only numbers?
@Chew Seong Cheong @Mark Hennings @Pi Han Goh
Please let us know how the solution above came to be. And please let us know how you would do it without using the graph.
First, they had misprinted the denominator terms. It should be 4 instead of 2 . Second, they should explain what they are going to do. Actually they have rotated the ellipse clockwise through 4 5 ° (which is the same as rotating the axes system counterclockwise through 4 5 ° ) about the z - axis.
Log in to reply
I agree. How can they expect someone to go through the JEE by giving a crap solution that no one can interpret and is written as though the person who wrote it was on meth?
I think what they've done is written 2 ! for 2 . If you interpret it like that, the solution makes sense, and matches the original equation. Essentially it's the same way I did it; their last line would read a = 2 4 (which is 8 ) and b = 2 3 .
Log in to reply
I've never seen that notation before, though. Is it used elsewhere in the textbook?
Log in to reply
Neither have I. It's such a weird notation. Maybe the guy who wrote the solution in the textbook was high on meth.
@Chris Lewis
sir can you post your solution.
Thanks in advance
Log in to reply
It's already posted.
Yeah; it's already posted. In my opinion, Chris' solution and Alak Bhattacharjya's should get top upvotes. Good solutions indeed.
Since the book says "Megacosm", I assume it's by Fitjee. I can't believe a solution by Fitjee is that bad.
Log in to reply
@Krishna Karthik Yeah bro sometime FIITJEE make mistake in questions, but the questions in the book are very good.
Log in to reply
Yes. The questions are actually well thought out. I love the questions. They're much better than crappy repetitive Australian systems like Jacaranda Plus.
My method isn't particularly creative, but it works.
x = r cos θ y = r sin θ
Note that r varies with θ . Plugging these into the equations and isolating r 2 yields:
r 2 = 1 6 1 + 2 sin θ cos θ + 9 1 − 2 sin θ cos θ 1
The area is then:
A = ∫ 0 2 π 2 1 r 2 d θ ≈ 1 8 . 8 5