What is the area of the blue triangle?
The line segments shown divide parallelogram A B C D into 8 regions, and the areas of the orange triangles are 48, 21, and 63.
What is the area of the blue triangle?
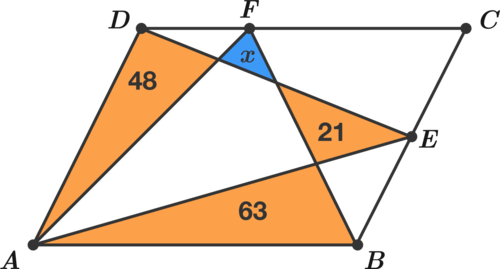
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
This doesn't mean that any parallelogram can actually exist with such regions having areas 48, 42, 63, 27, as how it appears in your figure. It would be nice if one did exist for verification. Can't find one yet.
Log in to reply
The numerical values for the triangular areas are actually derived from a real parallelogram with the points
A = ( 0 , 0 ) , B = ( 3 , 0 ) , C = ( 4 , 2 ) , D = ( 1 , 2 ) , E = ( 3 . 5 , 1 ) , F = ( 2 , 2 )
In addition, the sketch is even drawn to scale, so that in principle you could measure the solution.
Log in to reply
I used your coordinates for your parallelogram and scaled it up so that A 1 = 4 8 . I then found the following areas:
A
1
=
4
8
A
2
=
2
1
A
3
=
9
9
A
4
=
6
3
A
5
=
6
B
1
=
8
(white area upper left)
B
2
=
7
0
(white area upper right)
B
3
=
2
1
(white area lower right)
Total area 3 3 6
What I suspect is that you "found" the area A 2 to be twice 2 1 . From this, you deduced that A 5 = 2 7 , not 6 .
Also, in your problem statement, you wrote 68, when it should have been 63. See where you wrote "48, 42, 68".
Log in to reply
@Michael Mendrin – I made a typo, when I created the diagram... Now I have adjusted the number in the text accordingly. There might be no matching parallogram to the numbers, but now everything is consistent. Thanks, for the comment.
He was going j
NThank Viet g
How did you find A3?
Log in to reply
A3 cancels out so does not actually have to be found.
David meant that since A1 + A2 + A3 and A3 + A4 + A5 are equal to the same thing, you can cancel out A3, which leaves you with A1 + A2 = A4 + A5. Just a clarification :)
How do you make this graph with different colors for each region?
Log in to reply
I’m not sure how he did it, but one option would be to use Geogebra, a free geometry tool available as a webapp, a chrome app, and an iOS app (maybe android too I’m not sure).
I actually created the graphic in latex with the package tikz.
well, I'm confused isn't that A (ADF) =A3+A4+A5? You may mix them up, still thanx!
Log in to reply
You're right, I mislabeled the areas. It was still true, because both surfaces are the same anyway. But I've corrected that now.
how do you know abf or ade is half of abcd?
Log in to reply
create a point along AB which is a distance of DF away from A. Connect that point to F with a dashed line and all will be revealed; you’ll see 2 parallelograms, both bisected by the sides of ABF
i don't get it
Log in to reply
Read Daniel McShane's reply to the comment below. It's a good, concise explanation that is key to arriving at the answer.
AB & AD are not necessarily equal, so this logic is wrong even if the answer is correct.
Log in to reply
The line segments AB and AD are not equal. Only the triangles ABF and ADE have the same area.
how did u know "the two triangles and each have a height and a base side in common with the parallelogram, so that their areas are both equal to half the parallelogram area"???
Log in to reply
It is definition of area of triangle (St=base x height /2) and parallelogram (Sp = base x height). If you cannot see on current picture, imagine edge case - triangle is formed of 3 corners of parallelogram.
How did you get from A 5 = A 1 + A 2 − A 4 to 6 ?
Log in to reply
He plugged in the values for A 1 , A 2 , and A 4 given in the problem.
W.K.T , If a triangle and a parallelogram are on the same base and between same parallels, then the area of the triangle is half of the area of the paralellogram. So, from the above statement - a r ( A B F ) = 2 1 × a r ( A B C D ) ⋯ ( 1 ) Similarly, a r ( A E D ) = 2 1 × a r ( A B C D ) ⋯ ( 2 )
∴ , From equations (1) and (2) a r ( A B F ) = a r ( A E D ) ⋯ ( 3 ) Now, Let the area of the region enclosed between the orange shaded regions be ′ y ′ So, from equation (3) we get, 6 3 + y + x = 4 8 + y + 2 1 6 3 + x = 6 9 x = 6 9 − 6 3 x = 6
Is this true for all triangles whose base/height is within the parallels? I can see it's true for a triangle whose top point (say) bisects the upper boundary of the parallelogram. It's not intuitively obvious to me that this is also true as the top point of a triangle moves across the upper boundary (again, say) while the base remains still. Perhaps you can enlighten me? Good problem. Thank you.
Log in to reply
As the top point moves across the height remains the same.
Log in to reply
You are absolutely right @Luke Briggs And... @ted fedorowicz - This is a property of parallelogram
Log in to reply
@Prem Chebrolu – Thank you Prem. I agree I should have been able to intuit that but I didn't. Lesson learnt. Ted F
Thank you. Yes it's clearer now; the base and height do remain the same. I'll remember that. Ted F
Relevant wiki: Length and Area - Composite Figures
We must realize that Δ A D E and Δ A B F have the same area (it is half of the area of the parallelogram).
This is because the product of their bases and heights are the same due to their relation to the parallelogram.
Note that the quadrilateral is common among both figures.
Hence,
4 8 + 2 1 = 6 3 + x 6 9 = 6 3 + x x = 6
While the conclusion of the answer is correct, the bases and heights do not match. Only their product is equal, due to their relation with the parallelogram.
Log in to reply
Ah, I should clarify that the base of ADE is the height of ABF, and vice versa, as seen by the term “just interchanged”. But just in case, I edited that part. Thanks for the correction!
Let us assume that the white quadrilateral between the marked areas as y.(refer diagram if you have problem). Now let us shift point E to point C.(the point to observed is that the area of triangle AED doesn't change in doing so,as base and hieght are both constant). Similaly let us shift point F to point C. What we get to see is that a digonal is formed from A to the opposite point which you may call A,C or F. What is to be observed is that the area of the triangles formed are equal. (Diagonals bisect parallelogram).hence we proove that area of AED and AFB are equal. Now, let us come back to the original diagram. Remember, we assumed the white space as y. We get an equation. 48+y+21=x+y+63. Y cancels from both sides, and x=6, and that's our answer!!!!
I feel like a freak, I visualised it (I do a lot like this that way). I simply looked at X as being close to a third of 21. Then mentally rotated X into the corners of 21 and concluded it wasn't quite a third, but definitely more than a quarter. that doesn't leave many whole integers in that bracket that make sense. It had to be 6.
me too. i just saw all the numbers were multiples of three, and 9 was too large (at least three seem to fit, and 3x9=27 > 21), so 6 fit the bill. And that makes two even areas(6 and 48).
The triangles A B F and D E A have the same area, which is half of the parallelogram A B C D 's area. Both triangles contain that entire empty space in the middle, implying their leftover area when said empty space is removed is the same. Therefore, 48+21=63+x, implying x=6.
The triangles are all somewhat similar. 63-48=15, so 21-15=6. Further more each triangle is made of the same components so their area are equal.
Well I just added 48 and 21 and then subtracted the result from 63
x+W+63 = 48+W+21 ==> x=48+21-63 ==> x=6
As an alternate way to show △ A B F and △ A D E are congruent is that by moving one point on a triangle parallel to its base it’s area doesn’t change. By moving point E up to point C we can clearly see that it’s area is one half the parallelogram, and similarly with F and C . Once we know the areas are congruent we know that,
4 8 + 2 1 + A q u a d = 6 3 + A q u a d + x , x = 6
The answer has to come from the numbers 21, 48 and 63, so the only answer that made sense was 48+21-63! Bad maths, good logic
Relevant wiki: Length and Area - Composite Figures - Intermediate
The two triangles A B F and A D E each have a height and a base side in common with the parallelogram, so that their areas are both equal to half the parallogram area. If we divide the triangles into the areas A 1 , A 2 , A 3 , A 4 and A 5 as shown above, the result is A A D E A A B F ⇒ A 5 = A 1 + A 2 + A 3 = 2 1 A ABCD = A 3 + A 4 + A 5 = 2 1 A ABCD = A 1 + A 2 − A 4 = 6