What is the area of the polygon?
I have a polygon with a perimeter of 45 and can inscribe a circle with a maximum radius of 5.
What is the area of this polygon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great visualization to the solution Raymond! And the best part is, the area is independent of the number of sides for the polygon. However, is there a way to prove that all n-sided polygons (n>=3) can be used to solve this problem, or will the solution not be applicable after a certain point?
Thanks! When the inscribed circles are the same, the regular polygon has the shortest perimeter. Therefore, when n has the maximum value, the circumference of the polygon is 45cm. Let the radius of the inscribed circle be 5cm. Then 2 n × 5 × tan ( 2 n τ ) = 4 5 n tan ( n π ) = 4 . 5 n ≈ 3 . 4 0 1 9 1 0 5 So the maximum value of n is 3 ! In my solution I draw a quadrilateral...
Log in to reply
Thanks for the clarification!
You started your train of thought on the right foot but you must have been confused from there on because you got the conclusion backwards. In fact, what you would have shown with a correct reasoning and the above equation is that there exists no such triangle that fulfills the constraints of the problem and that any suitable tangential polygon must have more than three (that is, at least four) sides. In fact, by even the weak version of the isoperimetric inequality for triangles, there exists no triangle with has both the perimeter and the area you have in this problem, much less one with is a tangential triangle and with an inradius of some arbitrary length that you have given. In fact, a triangle with a perimeter of 45 cannot have area larger 225 sqrt(3)/4than and even in the most favourable shape the corresponding inradius cannot exceed in length the value of 5 sqrt(3)/2. Both of those values are significantly smaller than the values given in the problem (not that it matters how much smaller they are, of course - it doesn't matter by how much a fundamental inequality is not satisfied, merely that it is not satisfied). I guess the lesson here is that one always has to pay attention to the conditions under which a relationship holds, and existence is often overlooked but is in fact crucial - one cannot simply put arbitrary numbers into geometric relationships under a false assumption of universality of the equations without regard to the attached conditions. As an example: Following the perimeter formula in such a mindless way would tell one that a triangle with sides 2, 3 and 10 has a perimeter of 15. That is however completely false because the question itself is ill-defined: no such triangle exists at all, and you cannot draw such a triangle even if you try for eternity.
@Raymond Fang Then, what is the polygon which you mentioned in the problem.
Log in to reply
Well, what does "what is the polygon" mean? Are you asking me to say that change that "polygon" to "triangle" or specified place that is a triangle?
Log in to reply
I mean I do not know if the polygon is a triangle, quadrilateral, pentagon, etc.
Log in to reply
@. . – Oh, I know. The number of sides of the polygon has nothing to do with the result.
Log in to reply
@Raymond Fang – That is a strong statement to make in the best of cases in geometry, and here it is in fact demonstrably false. It has at least as much to do with it as to say that such a n-gon doesn't even exist for all n given the parameters of the problem. Though it would be correct to say that for the tangential polygons that do exist given the constraints you've put, the result is independent of the number of sides. You cannot sidestep the fact that they might not even exist though for a given n.
I approached this problem as a regular polygon. In that instance, the area of the polygon is 1/2AP where P is the perimeter and the apothem is equal to the radius of the inscribed circle. In the case of an irregular polygon, where an inscribed circle can be created, the area will also be equal to half of the inscribed radius times the perimeter.
The difficulty of this question is that I didn’t give a picture (I didn’t draw it on the title on purpose). You can draw a picture: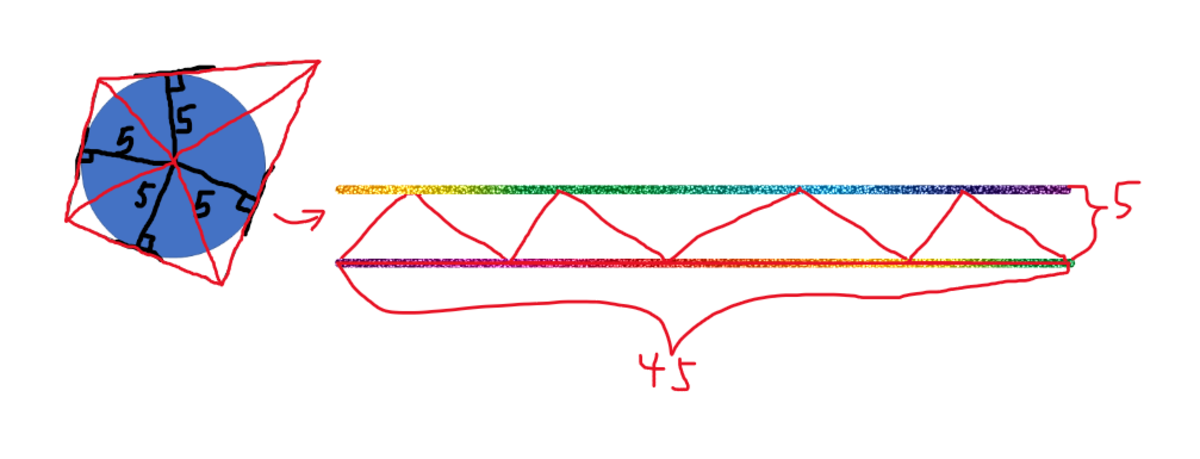
The area of the polygon is
4
5
×
5
÷
2
=
1
1
2
.
5
(
c
m
2
)
Note
: The number of sides is at most 3. Please ignore the quadrilateral here. The result is independent of the number of sides.