What is the area of the quadrilateral?
A B C D is a square and A E = B F = C G = D H .
What is the area of the orange quadrilateral D H M G ?
The answer is 102.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Could you explain why the pairs opposite of each other have the same area or provide a link please...?
Log in to reply
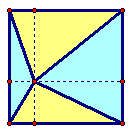
s =side length of the square. The two yellow triangles have the same base s and heights that together add to s . The two blue triangles also have the same base s and heights that together add to s .
Therefore the yellow area = blue area = 2 1 s 2
Log in to reply
If you had another square with equal baces(X,Y) and hight on each side would you still get X area= y area= 1/2 S2
Thank you for your explanation and diagram!
Brilliant!
I also solved just the same way.
Beautiful in its simplicity.
I don't yet get how you added those areas
Log in to reply
ar( E B F ) = ar( G C F ) = ar( H D G ) = ar( A H E ) = y . You understood that the the sum of pair of opposite triangles are equal. Therefore, ar( E F M ) + ar( H G M ) = ar( G M F ) + ar( H M E ). That implies, ( 6 0 − y ) + ( x − y ) = ( 9 3 − y ) + ( 6 9 − y ) . Therefore, 6 0 + x = 9 3 + 6 9 . So, x = 1 0 2
You seem to have skipped one or more steps between lines 2 and 3.
How do you know that EFGH is a square?.. All it's sides are equal.. that's okay, it doesn't mean that it's a square.. It can also be a rhombus.🤔
Log in to reply
Think about the angles of the four triangles and how they lead to the angles of EFGH.
No, it can't be a rhombus bcoz here in the square ABCD, you easily conclude that FH = GE.
Life hack:
You have 3 tries before you fail. This type of question usually uses integers. The total area of the square should be an integer squared. The known area is 93 + 60 +69 = 222 Likely possibilities: A) 34 ; Total area = 16^2 = 256 -> 256 - 222 = 34 B) 67 ; Total area = 17^2 = 289 -> 289 - 222 = 67 C) 102 ; Total area = 18^2 = 324 -> 324 - 222 = 102 D) 139 ; Total area = 19^2 = 361 -> 361 - 222 = 139
However, judging by the diagram 102 seems to be the most plausible answer.
After doing this cheeky trick you might want to see how the real problem solvers have done it so that you will not have to rely on approximations and luck next time
Log in to reply
Lol! 😂😄. Well done!
I did it on similiar lines - I added up the three given areas and had 222, and realised that 67 and 102 were the two most likely options for the missing area.
Oh,you 're very smart
Unfortunately, one has to previously know that the opposite triangles (in the inner square) add up the same area than the other pair, because it is not an intuitive result. So, you can not solve it just by "thinking out of the box" as Brilliant states. Just saying.
Log in to reply
You are right, this piece is missing. One way to see that it is true is to notice that moving M in a parallel direction relative to one of the sides of the small square leaves the sum of opposite triangles invariant. By two such moves one can bring M to the center of the small square, where the result becomes obvious.
Log in to reply
Or it should be given that M is at the horizontal CENTER of the larger square.
Intuitive Proof of EFGH is square: assume HA is tilted by some degree to make HE. Similar tilt has been made for other 4 sides. Hence, all tilted sides would be at 90* & equal in length. Let £ means triangle. Ar(£HEM) + ar(£GFM) = 1/2(HE x EF) where EF is sum of perpendicular distances of M from both the bases.
i just guessed it first try.... not quite sure how that happened
I guessed the answer also correctly. I guessed it because the area of a triangle is 1/2 h b. b is the same for all triangles. The addition of the h of 2 opposite triangles is equal to the square base. so the area of 2 opposite triangles is the same as the other 2.
Set up coordinates with A at the origin, and let B have coordinates ( X , 0 ) , and let M have coordinates ( a , b ) . Suppose that A E = x . Then A E M H + C G M F = ( 2 1 x b + 2 1 ( X − x ) a ) + ( 2 1 ( X − x ) ( X − a ) + 2 1 x ( X − b ) ) = 2 1 x X + 2 1 ( X − x ) X = 2 1 X 2 and hence X 2 = 3 2 4 , and X = 1 8 . But then D H M G = 2 1 X 2 − B F M E = 1 6 2 − 6 0 = 1 0 2
can you explain it through diagram? i am not getting the last equation.
Log in to reply
I showed that one pair of opposite quadrilaterals have total area equal to half the square. Thus the other two opposite quadrilaterals must have area equal to half the square as well.
I think that the last equation was intended to start with DHMG, instead of DHMC.
I got the same simply rotating a bit
Let H E = E F = F G = G H = c ; Δ A H E = Δ B E F = Δ C G F = Δ D G H = x and D H M G = y
Note that Δ A H E = 2 c h = 6 9 − x and Δ C F G = 2 c ( c − h ) = 9 3 − x
So we get c h = 1 3 8 − 2 x ; c 2 − c h = 1 6 8 − 2 x where h is the height of Δ A H E .
⟹ c 2 = 3 2 4 − 4 x
Similarly we get c 2 = 1 2 0 + 2 y − 4 x
Equating both equations
⟹ 3 2 4 − 4 x = 1 2 0 + 2 y − 4 x
⟹ y = 1 0 2 .
@Hans Gabriel Daduya you need to specify "h" that you have used in your solution!
Log in to reply
Ok thanks!!!
Log in to reply
@Hans Gabriel Daduya how did you find the area of triangle AHE using height and hypotenuse?
Log in to reply
@Moulik Bhattacharya – He means the triangle MHE, not AHE. Just replace M with the corners and you can read it properly.
well ,the sum of the total area should be a perfect square.(side * side for a square) 69+93+60+x=perfect square. where x is the answer. rest is hit and trial. we have two appropriate perfect squares 289 and 324 which can be used.
Log in to reply
Exactly - two serious possibilities and three attempts allowed = too easy to be considered interemediate.
why not 225? the area can be 3 in that case..
Maybe I'm missing something here but how can triangle AHE = 69-x and triangle CFG = 93-x if you defined both triangles equal to x?
Log in to reply
Ah! I think there's a typo. Triangle MHE = ch/2 = 69 - trangle AHE = 69 - x, where h = height of MHE where HE = c is the base.
Empirically the area of square must be (side) squared. Known area of quadrilaterals is 222 and orange area largest, so must be larger than (16) squared. Logic shows (17) squared not large enough and (19) too large. Answer is (18) squared = 324. Orange = 324-222=102.
Finally the least confusing and simplistic answer which doesn't require my brain to work out maths!! Thank you!!
That's exactly how I solved it!
But why the side of the square must be a whole number?
Again, guessing instead of proving...
Join the vertices
M
and each of
A
,
B
,
C
and
D
by a line segment.
Let [ X Y Z ] denotes the area of the polygon X Y Z .
Suppose A E : E B = 1 : p . Then B F : F C = C G : G D = D H : H A = 1 : p .
Suppose [ A E M ] = r , [ B F M ] = s , [ C G M ] = t and [ D H M ] = u . Then [ B E M ] = p r , [ C F M ] = p s , [ D G M ] = p t and [ A H M ] = p u .
We have the following:
[ B F M E ] [ C G M F ] [ D H M G ] [ A E M H ] = = = = p r + s p s + t p t + u p u + r r + t = = = = = 6 0 9 3 ? ? 6 9 s + u
Hence, ( p t + u ) + ( p r + s ) = = = p ( r + t ) + ( s + u ) p ( s + u ) + ( r + t ) ( p s + t ) + ( p u + r )
This means that [ D H M G ] = p t + u = ( p s + t ) + ( p u + r ) − ( p r + s ) = 9 3 + 6 9 − 6 0 = 1 0 2 .
@Chan Lye Lee I solved this in exactly the same way!!!!
It therefore follows that the point M can be determined uniquely,i.e. - distance from LH edge = 69/9 - distance from RH edge = 93/9 - distance from top edge = 102/9 - distance fro bottom edge = 60/9
However, the distances AE=BF=CG=DH cannot be determined uniquely!
Simply I solved by area square thought. Total area should be in the square format as it is sqaure. There are 225,256, 289 and 324 around that one( sum of remaining is 222 ). It is closed to 93 as it is opposite to that one (and it seems to be also). So 324 is the utopian one which gives the answer as 102 which is around 93. ( 324- 102)
Because this site is all about guessing and not proving
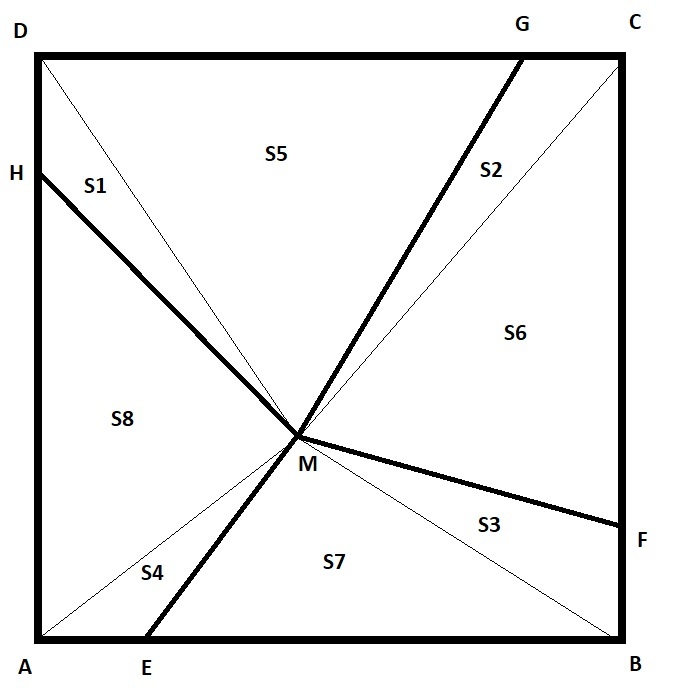
S1 + S3 = S2 + S4
S5 + S7 = S6 + S8
Add up these two equations
(S1 + S5) + (S3 + S7) = (S2 + S6) + (S4 + S8)
S1 + S5 + 60 = 93 + 69
S1 + S5 = 102
Consider eight triangles: DGH, AHE, BEF, and GFC are all clearly identical. That leaves HME, GMF, EMF, and EMG.
The formula for an area of a triangle is (base*height)/2, where base and height are defined perpendicular to each other and in the plane of the triangle. The bases of all the unknown triangles are the lines HE, EF, FG, and GH, and must be identical due to the side lengths of ABCD and the AE=BF=CG=DH equivalences.
Now consider the square HEFG. Drawing lines through M perpendicular to the square will produce the height lines of the triangles, and these heights don't need to be directly calculated - the line passing from GH to EF through M must be the same length as the line passing from HE to FG passing through M. The formula A=bh/2 thus means that the areas of HME+GFC equals the areas of EMF+HMG. The identical triangles can be added to this, meaning that HMEA+GCFM=EMFB+HMCD.
Solving for HMCD produces HMCD=HMEA+GCFD-EMFB=69+93-60=102
This is not a very reliable method for future problems but someone will probably find it useful: First I tgought that the area of the square has to be the square of some number, so I added the known areas first, that is 222. Then I compared the area of DHMG to MFCG, and DHMG had to have an area equal or lager than MFCG, so I added 93. 315 was the minimum area of the square, so I rounded up to the closest square number, that was 324, or 18^2. After that I remained with 69+60+93+x=324. x=102.
Basically, I supposed the square was drawn to scale with each side being an integer. It seemed probably that the square was 18x18 = total area of 324.
The area can be presumed to be a square of a natural number. Since DGHM looks bigger than CGMF the nearest possible number that would lead to a square of 18×18=324 area would be 102: 102+60+69+93=18×18
I noticed all areas where divisible by three. And the blank one seemed bigger than the one with 93, so I first tried 99, that was false. Then I tried 102 and that was correct. A little educated guessing :p
I just guessed squares and subtracted the area from each result until I got a solution just bigger than 93, as that’s the way it looks to me. I landed on 18x18, which is 324, subtract 222 (60+69+93) from that and end up at 102.
69-60+93=102, that is wassup,
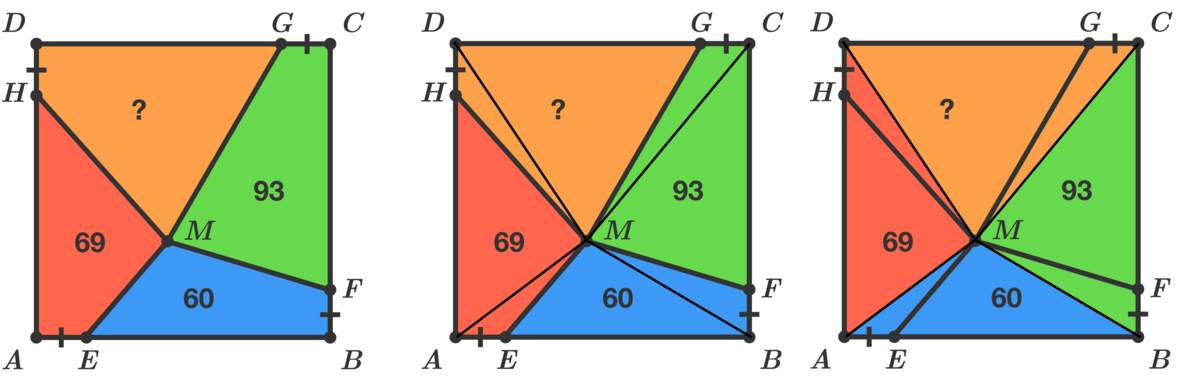
This is my solution: Let the small length be a and the side of square be L : Since G C M + A E M = 2 1 a L = D M H + B M F
So we can swap the color as the right figure, so ? + 6 0 = 6 9 + 9 3 Obtain the answer ? = 1 0 2 .
Total area of the given parts = 222.
The square numbers great than 222 are 225, 256, 289, and 324.
324 - 222 = 102
This is the suitable solution.
Another approach using estimation: assuming the sides of the square are integers, and judging the orange area slightly larger than the green area, around 10%, say 100. Total Area is then an estimated 69+93+60+100=322. Then I try approaching the answer: Sides are 17 then 17x17=289 Sides are 18 then 18x18=324 (very close)
Therefore I assume the sides to be 18, resulting in an area for the orange area of 324-(60+69+93) = 102
Because there is only one solution, the lengths of A E , B F , C G , and D H should not matter. To simplify things, we assume that A E = B F = C G = D H = 0 . Again, to find the answer, it does not matter what we set the lengths to, as long as the given conditions in the problem are satisfied. Now, we get four triangles which have areas of 6 9 , 6 0 , 9 3 , and an unknown area. Let the distance that M is from A D be m . Adding the areas of the red and green triangles together, we get 2 x m + 2 x ( x − m ) = 2 x ( m + x − m ) = 2 x 2 = 6 9 + 9 3 = 1 6 2 . We know that x 2 is the area of the square, so the area is 2 ⋅ 1 6 2 = 3 2 4 . We can find the area of the orange area by subtracting the area of the entire square by the area of the red, blue, and green. Doing so gives an answer of 3 2 4 − 6 9 − 9 3 − 6 0 = 1 0 2 .
A r e a ( D H M G ) = 1 0 2