What is the minimum distance between a point on one torus and another point of the other torus?
This problem's question: What is the minimum distance between a point on one torus and another point of the other torus?
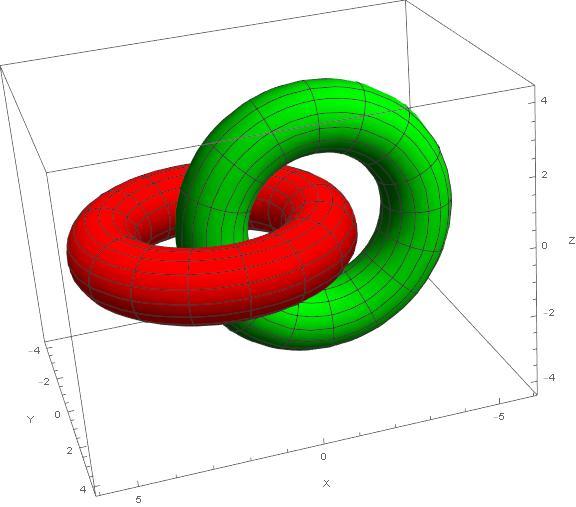
The set of parametric functions describing the first torus is { cos ( u ) ( cos ( v ) + 3 ) + 2 3 , sin ( u ) ( cos ( v ) + 3 ) , sin ( v ) } . This torus is red in the image, if that is important to you.
The set of parametric functions describing the second torus is { cos ( u ) ( cos ( v ) + 3 ) − 2 3 , − sin ( v ) , sin ( u ) ( cos ( v ) + 3 ) } . This torus is green in the image, if that is important to you.
The equations were adjusted to make the form of the answer very simple. This information may be useful.
The answer is 1.000000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thank you for the problem! It is a nice one. Based on the parametric curves provided in the question, I obtain an answer of 3 as opposed to your answer of 1. I request you to check the expression for the Euclidean distance. If I happen to be wrong, please tell me my mistake.
Also, I see a ' cos ( v ) − 3 ' term in the expression for distance that you have obtained. If I understand correctly, based on the description of the curves, there is no such term.
Log in to reply
Upon further inspection, I see that the parametric coordinates of the tori are different in your solution as compared to that described in the question. I request that this problem be rechecked.
Log in to reply
The only significant problem in the entire solution was the misquote of p1 by its negative. It turns out the correct value of p1 was used through the remainder of the solution (or explanation)
Log in to reply
@A Former Brilliant Member – Thank you for looking into the problem. Unfortunately, I am still not convinced. I tried framing the equation for the Euclidean distance between the position vectors p 1 and p 2 x . The expression that I obtain after multiple cross checks is different from the one written in your solution. Maybe I am doing some very simple mathematical operations completely wrong, but I still request you to check the expression for the distance between the two parametric coordinates.
Log in to reply
@Karan Chatrath – I have checked it yet again. There is nothing wrong with that expression. The only possible issue is that the last two summands are reversed. As addition is commutative, this is of no consequence. Six people, including myself, have solved this problem.
Post your formula for the Euclidean distance so that may I can then guess what the issue is.
Log in to reply
@A Former Brilliant Member – Thank you for taking out time to address this.
We have:
Parametric coordinates of the first Torus: x 1 = cos ( u ) ( cos ( v ) + 3 ) + 2 3 y 1 = sin ( u ) ( cos ( v ) + 3 ) z 1 = sin ( v )
Parametric coordinates of the second Torus: x 2 = cos ( r ) ( cos ( s ) + 3 ) − 2 3 y 2 = − sin ( s ) z 2 = sin ( r ) ( cos ( s ) + 3 )
The distance between the points is: D = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2
Which simplifies to:
D = ( cos ( u ) ( cos ( v ) + 3 ) − cos ( r ) ( cos ( s ) + 3 ) + 3 ) 2 + ( sin ( u ) ( cos ( v ) + 3 ) + sin ( s ) ) 2 + ( sin ( v ) − sin ( r ) ( cos ( s ) + 3 ) ) 2
Now, substituting u = v = r = s = 0 , we get: D = ( ( 1 + 3 ) − ( 1 + 3 ) + 3 ) 2 + 0 + 0 Which leads us to the answer of 3
Log in to reply
@Karan Chatrath – I entered your distance formula and verified for myself that it returns 3 for u → 0 , v → 0 , r → 0 , s → 0 .
For the first summand and ignoring the squaring operation for the time being, I find differences. I expanded the expression to make the difference more apparent:
Mine: cos ( r ) ( − cos ( s ) ) − 3 cos ( r ) − cos ( u ) cos ( v ) + 3 cos ( u ) + 3
Yours: cos ( r ) ( − cos ( s ) ) − 3 cos ( r ) + cos ( u ) cos ( v ) + 3 cos ( u ) + 3
The difference, subtracting mine from yours: 2 cos ( u ) cos ( v )
There are sign differences. Please, check your signs.
Log in to reply
@A Former Brilliant Member – The distance formula is different (from that of yours) because the formula I have used is the one based on the given parametric coordinates. Your distance formula is based on a set of parametric coordinates that is not similar to the ones given in the question.
In your solution, I once again request you to see the expressions p 1 and p 2 x . The expressions in red and green. The expression that follows that is Δ = p 1 − p 2 x . This expression is the one based on which you have computed the distance formula. This expression is where I see that something is not right.
The first element of the expression Δ that you have typed is: − cos ( r ) ( cos ( s ) + 3 ) − cos ( u ) ( cos ( v ) − 3 ) + 3
According to me, by looking at the x coordinates of each torus (according to the coordinates typed in the problem statement), it should be:
− cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) + 3 ) + 3
I have verified this with a symbolic toolbox using a computer.
I will definitely cross check my work once again, if necessary. As you correctly pointed out, many people have solved the problem. But I am still not convinced.
Log in to reply
@Karan Chatrath – I discovered that I had overlooked mentioning a change I made in the p1 formula to bring the numerical solution to all zeroes. This caused our differences. These differences are insignificant in determining the minimum distance. For that, see the addendum of 2019 June 2 0900Z. There are many distance 1 solutions. For the original p1 and using your version of the distance formula, ( − cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) + 3 ) + 3 ) 2 + ( sin ( v ) − sin ( r ) ( cos ( s ) + 3 ) ) 2 + ( sin ( s ) + sin ( u ) ( cos ( v ) + 3 ) ) 2 /. { u → 0 , v → π , r → 0 , s → 0 } ⇒ 1 .
Log in to reply
@A Former Brilliant Member – This clarification was helpful.
It means that the equation for distance has multiple local minima in the parameter space. I have overlooked this point once before while solving an optimization problem. Now I know better.
I ran a simple computer code that searches for the minimum when all independent parameters are varied between − 2 π and 2 π in steps of π / 1 0 0 . The correct answer is indeed equal to 1 .
Thank you!
Added 2019 June 2 0900Z:
I awoke in a nightmare about this problem.
A slice through the tori on the z = 0 plane.
A similar slice exists on the y = 0 plane.
The bright red circle, which is the innermost circle going around the red torus, surrounding the darker green circle within is at distance 1 from corresponding points on the darker green circle. Also the closest point on the lighter green circle is distance 1 from the darker red circle, which is the outermost circle going around the red torus.
Therefore, there are an uncounted infinite of points at which the distance is 1 .
ParametricPlot ⎣ ⎢ ⎢ ⎡ ⎝ ⎜ ⎜ ⎛ 2 cos ( u ) + 2 3 4 cos ( u ) + 2 3 cos ( u ) + 2 3 − cos ( u ) − 2 9 2 sin ( u ) 4 sin ( u ) − sin ( u ) − sin ( u ) ⎠ ⎟ ⎟ ⎞ , { u , 0 , 2 π } , PlotStyle → { Red , Darker [ Red ] , Darker [ Green ] , Green } ⎦ ⎥ ⎥ ⎤
A simple examination of the parametric equations reveals that they are all circles and the first three are concentric.
And, this is a far simpler solution to the problem.
End of 2019 June 2 0900Z addendum.
Added 2019 June 11 1745Z.
In fact, the entire two annuli regions, in blue, are of distance 1. The two annuli intersect in a line segment between the two tori, which is where my original solution is.
End of 2019 June 11 1745Z addendum.
The material below was edited 2019 June 4 1700Z to amplify and clarify several points.
First, I did a numerical minimization. The equivalent could be done by examining the plot given in the problem and then, using descending sized steps, search for the variables u and v to find values close to where the solution must be.
To do the numerical minimization, I changed the u and v in the second (green) parametric equations to r and s , respectively. This is necessary so that the positions on the two tori are independent. This is a four -dimensional optimization problem.
The p1 formula has had π added to v to bring the solution to all zeroes. Mea culpa: I forgot to mention this when writing this solution. Added: 2019 Jun 5 1600Z. This does not affect the minimum distance; it only affects the values of u, v, r and s at which this solution occurs. Please note well the addendum of 2019 June 2 0900Z above.
p1 = { cos ( u ) ( cos ( v ) + 3 ) + 2 3 , sin ( u ) ( cos ( v ) + 3 ) , sin ( v ) }
p2x = { cos ( r ) ( cos ( s ) + 3 ) − 2 3 , − sin ( s ) , sin ( r ) ( cos ( s ) + 3 ) }
Δ = p1 − p2x ⇒
{ − cos ( r ) ( cos ( s ) + 3 ) − cos ( u ) ( cos ( v ) − 3 ) + 3 , sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) , sin ( r ) ( − ( cos ( s ) + 3 ) ) − sin ( v ) }
Computing the Euclidean distance using the vector dot product:
Δ . Δ ⇒
( − cos ( r ) ( cos ( s ) + 3 ) − cos ( u ) ( cos ( v ) − 3 ) + 3 ) 2 + ( sin ( r ) ( − ( cos ( s ) + 3 ) ) − sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2
The equation above is the same equation given by the Wolfram Mathematica 12 EuclideanDistance function with absolute function replaced by the identity function as the problem is using real numbers and the square of a real is always non-negative.
EuclideanDistance [ p1 , p2x ] /. Abs → Identity ⇒ ( − cos ( r ) ( cos ( s ) + 3 ) − cos ( u ) ( cos ( v ) − 3 ) + 3 ) 2 + ( sin ( r ) ( − ( cos ( s ) + 3 ) ) − sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2
NMinimize [ { EuclideanDistance [ p1 , p2x ] , 0 ≤ u < 2 π ∧ 0 ≤ v < 2 π ∧ 0 ≤ r < 2 π ∧ 0 ≤ s < 2 π } , { u , v , r , s } , AccuracyGoal → 3 0 ]
The values returned are all very close to 0 or 2 π ; hence, the simplification to 0 .
Considering that trigonometric functions are being used, it seems that u , v , r and s are all 0 . Now to show that that is a solution.
The plot below contains small patches of the red and green tori. The orange line is the solution indicated by the numerical minimization. The ends of the orange line are the points { { 2 7 , 0 , 0 } , { 2 5 , 0 , 0 } } ) .
First, develop an equation for the Euclidean distance between arbitrary points on the two tori:
d = ( − cos ( r ) ( cos ( s ) + 3 ) − cos ( u ) ( cos ( v ) − 3 ) + 3 ) 2 + ( sin ( r ) ( cos ( s ) + 3 ) + sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2
Now, compute the derivatives of the Euclidean distance with respect to each of the variables, respectively:
eu = ∂ u ∂ d = − ( cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) − 3 ) − 3 ) 2 + ( sin ( r ) ( cos ( s ) + 3 ) + sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2 ( cos ( v ) − 3 ) ( sin ( u ) ( cos ( r ) ( cos ( s ) + 3 ) − 3 ) + sin ( s ) cos ( u ) )
ev = ∂ v ∂ d = ( cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) − 3 ) − 3 ) 2 + ( sin ( r ) ( cos ( s ) + 3 ) + sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2 sin ( v ) ( cos ( u ) ( − ( cos ( r ) ( cos ( s ) + 3 ) − 3 ) ) + sin ( s ) sin ( u ) + 3 ) + sin ( r ) ( cos ( s ) + 3 ) cos ( v )
er = ∂ r ∂ d = ( cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) − 3 ) − 3 ) 2 + ( sin ( r ) ( cos ( s ) + 3 ) + sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2 ( cos ( s ) + 3 ) ( sin ( r ) ( 3 − cos ( u ) ( cos ( v ) − 3 ) ) + cos ( r ) sin ( v ) )
es = ∂ s ∂ d = ( cos ( r ) ( cos ( s ) + 3 ) + cos ( u ) ( cos ( v ) − 3 ) − 3 ) 2 + ( sin ( r ) ( cos ( s ) + 3 ) + sin ( v ) ) 2 + ( sin ( s ) − sin ( u ) ( cos ( v ) − 3 ) ) 2 − sin ( s ) ( cos ( r ) ( cos ( u ) ( cos ( v ) − 3 ) − 3 ) + sin ( r ) sin ( v ) + 3 ) − cos ( s ) sin ( u ) ( cos ( v ) − 3 )
Note that eu , ev , er and es are equations into which specific values can be substituted.
Then. check that the derivatives are all zero when the variables are all zero (the suspected answer).
eu = 0 ∧ ev = 0 ∧ er = 0 ∧ es = 0 /. { u → 0 , v → 0 , r → 0 , s → 0 } ⇒ True
That check is successful.
Then, evaluate the Euclidean distance formula developed above to get the answer to the problem.
d /. { u → 0 , v → 0 , r → 0 , s → 0 } ⇒ 1
The answer is 1 .