What is the overlap width of these two semicircles?

Geometry Level 2

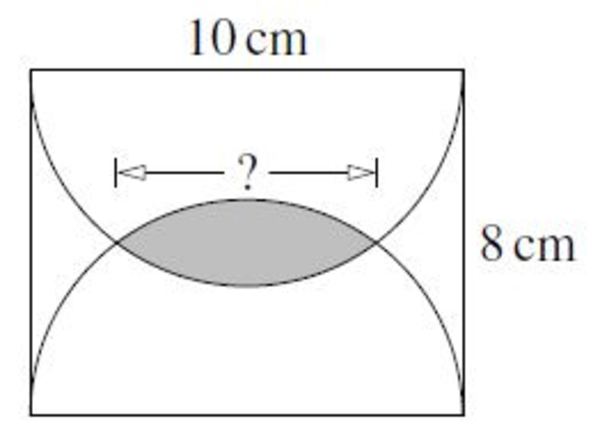Two similar (rotated) semicircles are drawn in a rectangle as shown. What is the width of the overlap of the two semicircles?

Source: Paralell

6.4 cm Not enough information 6 cm 4√2 + 𝜋/10 cm 2𝜋 (tau) cm 4√2 cm

1 solution

A Former Brilliant Member
Feb 5, 2020

To make it easier to explain, let's assign letters to the points. Let P, Q be the midpoints of the longer sides of the rectangle. Let R, S be the points where the semicircles meet. Let T be the point where PQ meets RS.

Each of the semicircles has a radius of 5 cm. Therefore PR, PS, QR and QS all have length 5 cm. Therefore PSQR is a rhombus. Hence the diagonals PQ and RS bisect each other at right angles. It follows that PT and QT each have a length of 4 cm. Let the common length of RT and ST be x cm.

We now apply Pythagoras’ Theorem to the right-angled triangle PTR. This gives 42+x2=52, and hence x2=52−42=25−16=9. Therefore x=3. It follows that both RT and ST have length 3 cm. Hence the length of RS is 6 cm. Therefore the width of the overlap of the two semicircles is 6 cm.

You can solve $x^2+y^2=5^2$ and $x^2+(y-8)^2=5^2$ , where $x=\pm 3\, \mathrm{cm}$ and $y=4\, \mathrm{cm}$ .

Sebastián Vidal Romero - 1 year, 4 months ago

Epic! I 95% get you

A Former Brilliant Member - 1 year, 4 months ago

How do you get y=(y-8)?

A Former Brilliant Member - 1 year, 4 months ago

Those equations describes two circumferences of radius $5\, \mathrm{cm}$ with its origins displaced $8 \, \mathrm{cm}$ along the vertical axis. You can solve for $y$ computing the difference between both and then solve for $x$ .

Let me know if you understand it! 😁

Sebastián Vidal Romero - 1 year, 4 months ago

@Sebastián Vidal Romero – Thank you - I think I remember the equation now :)

A Former Brilliant Member - 1 year, 4 months ago

What is the overlap width of these two semicircles?

1 solution

0 pending reports