An algebra problem by Aly Ahmed

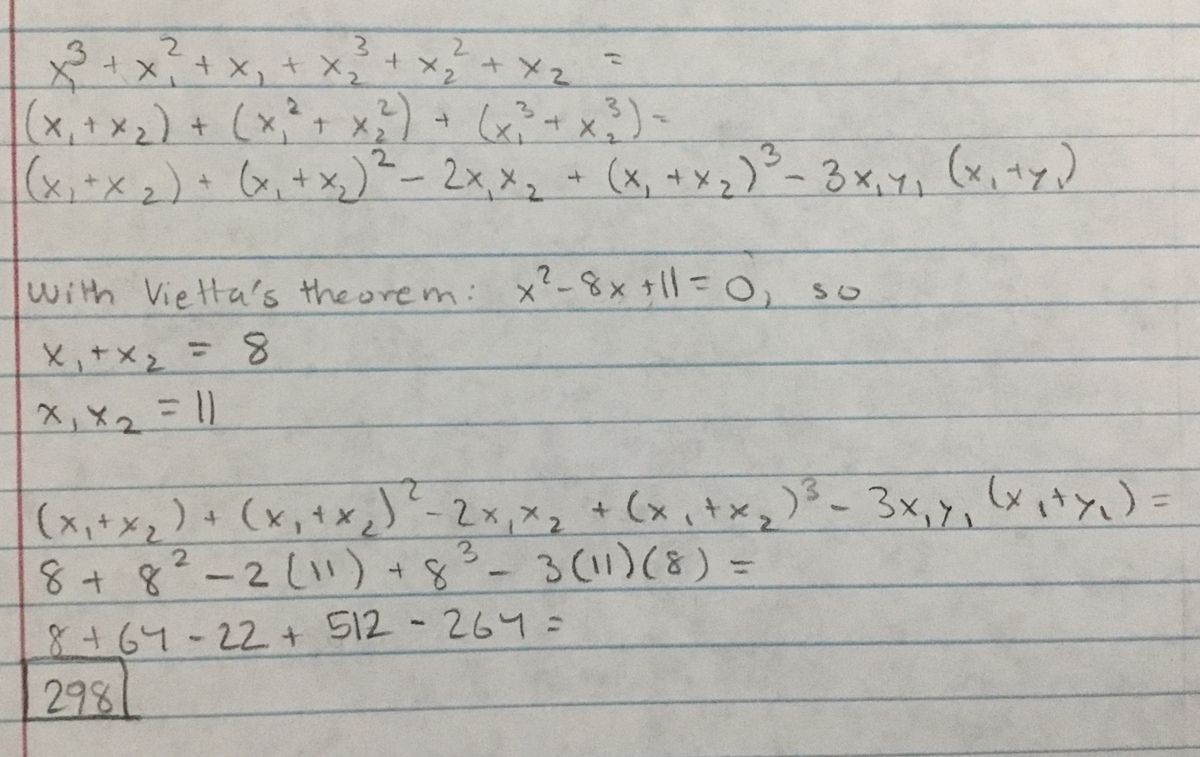
Given that:

$\begin{aligned} x^2 - 8x + 11 & = 0 \\ \implies x^2 & = 8x - 11 \\ x^3 & = 8x^2 - 11x \\ & = 8(8x-11) - 11x \\ & = 53x - 88 \\ \implies x^3 + x^2 + x & = 62x - 99 \end{aligned}$

Since $x_1$ and $x_2$ are the roots of $x^2-8x + 11$ , the sum:

$\begin{aligned} S & = x_1^3 + x_1^2 + x_1 + x_2^3 + x_2^2 + x_2 \\ & = 62x_1 - 99 + 62x_2 - 99 \\ & = 62 \blue{(x_1+x_2)} - 198 & \small \blue{\text{By Vieta's formula }x_1+x_2 = 8} \\ & = 62 \blue{(8)} - 198 \\ & = \boxed{298} \end{aligned}$

---

Reference: Vieta's formula