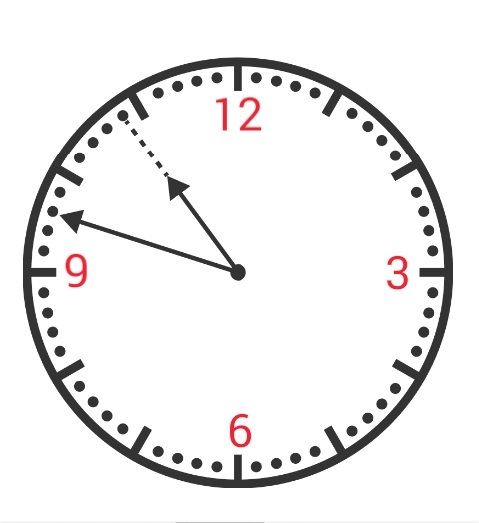
What time is it?
A clock with no numbers fell to the ground.
What time is it?

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
You cannot add or subtract time (apart from duration), so your answer is wrong
Log in to reply
The weekly problems including this one are checked by more than 10 Brilliant moderators including me before releasing. You understanding is wrong.
Log in to reply
No. I mean in your solution
It would be more proper if you told "12 minutes before 11"
Chew-Seong -- Do you check ALL of the weekly problems, contributed by others as well as yourself ?
Log in to reply
@Jesse Otis – Usually look through but do not try all. Why?
Log in to reply
@Chew-Seong Cheong – You do such a great job at posting problems and solving them I thought that maybe Brilliant recruited you to help them 'from afar'. :-)
Log in to reply
@Jesse Otis – We are appointed as moderators by Brilliant. We contribute for free. If you are active enough by contributing problems or solutions, you will be appointed as a moderator too.
If that actually happened then the answer is most likely correct
No idea what u r talking about
Actually, i didn't add or subtract time. I just added and subtracted numbers and not time. You just failed to see it.
Beautiful, and simple!!!
I found I was able to orient the clock so that every answer was possible. Unless someone can see a remedy to this every answer seems possible.
Log in to reply
It is not possible to do this. The time has to be twelve minutes from the hour due to the position of the hour hand.
Log in to reply
you are absolutely right -- my error was look only at the minute hand -- the relationship between the hour and minute was key, thus 10:48 was the only choice satisfying this relationship. I think it is interesting that 10:48 is only a potential answer, as there are 12 potential :48 points. Thus it is true that you cannot say what the time on the clock was, unless perhaps you looked on the back side and there was a point of suspension and you accepted the implication it was suspended from that point.
Log in to reply
@Cornelius Cooper – Actually, this is also not true. Note that in twelve minutes, the hour hand will be on an hour marking, so the minute hand MUST be on the 12 in 12 minutes.
Log in to reply
@Zain Majumder – I said when the hour-hand is at the hour mark, the minute-hand must be at the 12-hour mark. I didn't say it must be after 12 minutes.
Log in to reply
@Chew-Seong Cheong – It's the same thing; the hour hand must move a fifth of an hour (12 minutes) to get to the hour mark, and at that point the minute hand will be on the 12.
Log in to reply
@Zain Majumder – I don't understand what you don't understand, then.
Absolutely crazy! Great explanation and it already has me looking at things differently. At first glance I thought this was a trick question...mind blown!
this makes no sense. a clock falls to the ground how much does it weigh? like who knows when it fell to the ground and how much time has elapsed. you've provided a minute amount of the necessary info to make that assumption ultimately your question is only answerable with multiple choice and a selection process
Log in to reply
Since the clock has no AC cord it must be battery operated with an AA cell battery. This indicates the angle of descent and crash forced the AA cell battery to be jarred lose and thereby stop the forward motion of the minute hand. From this we use 24/2 to determine what you ate for lunch.
Wow i never thought like that I get it
It was not clear what "fell to the ground" entails. I thought it meant that the hour and minute hands got knocked and rotated by some angle.
The hour hand is 5 4 of the way between hour marks, and since 5 4 ⋅ 6 0 = 4 8 , that means the time is some hour and 4 8 minutes.
Since the minute hand must point to 4 8 , the hour mark between the given minute and hour hand must be 1 0 , so it is 1 0 : 4 8 .
 THIS PICTURE WILL BE OBTAINED IF WE ROTATE THE GIVEN PICTURE AT 180°.
THIS PICTURE WILL BE OBTAINED IF WE ROTATE THE GIVEN PICTURE AT 180°.
But why must we rotate the picture? Is it me, or is this question unclear?
Log in to reply
Thomas Sutcliffe Sep 18, 2018
The 5:23 and 11:53 options can be ruled out by observing the relative positions of the hour and minute hands. Brief observation shows that the clock cannot be the right way up was the hour hand is far too far beyond 4 o'clock (it is almost at the next hour instead of being about a third of the way round) for it to be 4:18. Having ruled out three possibilities we are left with 10:48 being the answer - and the minute and hour hands are the in the right relative positions for that.
we do not know the time to begin with....
Attempted in the same way.
...and this clock says NINE 48, not 10:48...
Log in to reply
Explain? You do know that the little hand is the hour hand right?
One of the easiest question on Brilliant. Use elimination and you'll get your result easily. Pay little attention on hour's hand and by intuition, answer is 10:48.
Pipe down, mate.
The clue is the minute hand (large one), which shows that the time must be 4/5 of an hour past the last hour. Therefore the time must be one in which the minutes are 4/5 of 60 = 48. Ed Gray
The hour hand is about to reach the next hour. Therefore, the minutes must not be less than 30. We have 10:48 and 11:53 as potential solution. But if the solution is 11:53 then the minute hand must be on the right side of the hour hand. So that reduces to 10:48.
I agree that it's 10:48, but I don't agree that "if it's 11:53 then the minute hand must be on the right side of the hour hand." That doesn't make sense to me. If it was 11:53 it would look almost identical, but the hour hand would be slightly past the hour mark, instead of directly aligned with it.
The hour hand is 4/5 of the way to the next hour. Because 60/5=12 therefor the minutes must end in 48, or 4*12.
Hour hand is nearing an hour. This means the minute hand should be nearing the 12.
In between two hour location is divided by 4 dots. Hence five segments. 60/5 = 12. Hence every 12 min hour hand travels one segment.
Since hour hand is still to travel one more segment to reach another hour point the minute hand must be 12 min away from hour point 12. Hence hour 12 is located. From there when we calculate for current location of hour hand we find it is reaching 11.
Hence correct answer is 10:48.
solution without using the full hour indicators on dial
| a … | angle to 12 o'clock | |||
| Z … | angle of minute hand | Z = | 6 0 3 6 0 ° *m - a | (1) |
| z … | angle of hour hand | z = | 1 2 3 6 0 ° *(h+ 6 0 m ) - a | (2) |
| z - Z | = 6 * 6 0 3 6 0 ° = 36° | (3) (from graph) |
| h … | current hour |
| m … | current minute |
(1) and (2) in (3) : 1 2 3 6 0 ° (h+ 6 0 m ) - a - 6 0 3 6 0 ° m + a = 36°
m = (30 * h - 36) * 1 1 2 ... must be integer -> only valid for h = 10, therefore m = 48
If minute-hand=x, and hour-hand=y x=y/12 so y=12x, when y need step 1 to next hour, the x (step 12 and) reach the 60th minute. Which at that time is 11:00. So y=11-1, and x=60-12, wich is 10:48.
A subtle thing to know about clocks is that when the minute hand is nearing twelve, the hour hand is quite close to the upcoming hour. In the above clock, the minute hand isn’t even last halfway, yet the hour hand is close to the next hour.
If you rotate and play around with the orientation of your screen, you’ll find that a 180 degree rotation of your screen (sorry if you’re on a computer) will produce a situation where the minute hand is nearing twelve and the hour hand is close to the next hour.
Read the clock and you get 10:48.
I f y o u l o o k c a r e f u l l y y o u w i l l s e e t h a t t h e r e a r e 1 2 m i n u t e s t i l l t h e n e x t h o u r . T h e o n l y a n s w e r t h a t i s w i t h 1 2
m i n u t e s t i l l t h e n e x t h o u r i s 1 0 : 4 8 .
The 5:23 and 11:53 options can be ruled out by observing the relative positions of the hour and minute hands. Brief observation shows that the clock cannot be the right way up was the hour hand is far too far beyond 4 o'clock (it is almost at the next hour instead of being about a third of the way round) for it to be 4:18. Having ruled out three possibilities we are left with 10:48 being the answer - and the minute and hour hands are the in the right relative positions for that.
It takes the hour-hand 12 minutes to move a small division of the dial. Therefore 12 minutes later, the hour-hand will be at an hour mark and the minute-hand will be at the bottom hour mark. When the hour-hand is at an hour mark, the minute-hand must be at the 12 hour-mark. Therefore, the time is 1 1 : 0 0 − 0 : 1 2 = 1 0 : 4 8 .