What's 7 Doing In There?
x can be expressed as b a , where a and b are coprime positive integers.
What is a + b ?
Note: Synthetic proofs welcome.
The answer is 157.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
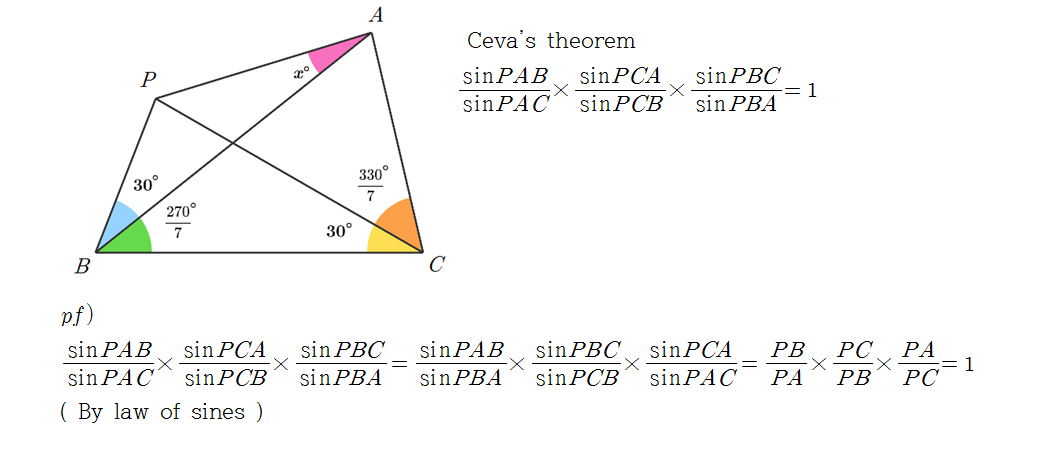
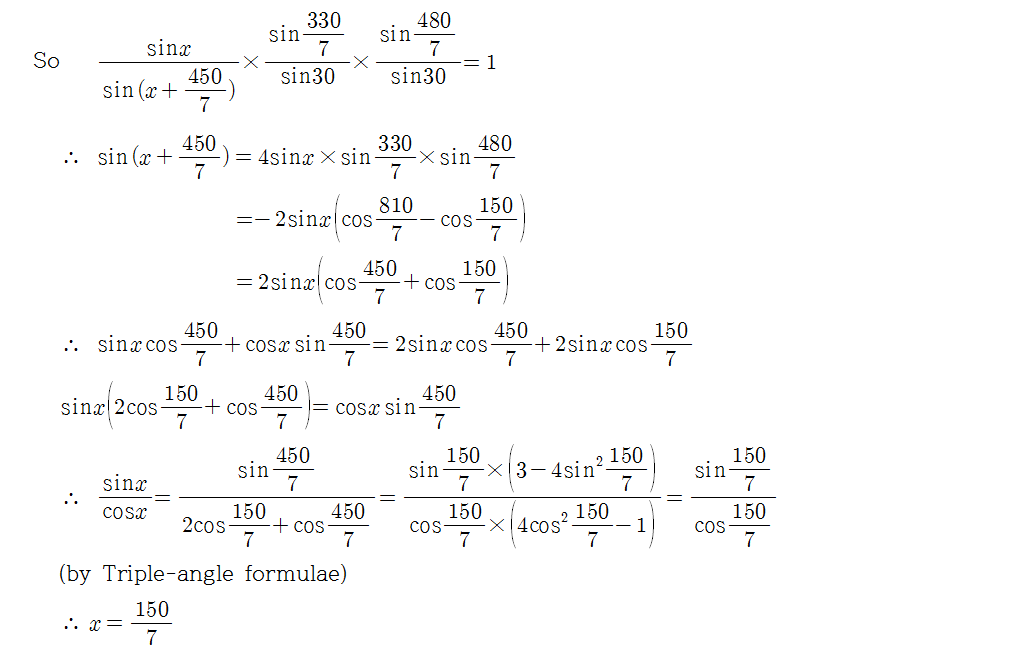
Excellent solution, direct derivation of x from known angles. If you don't mind, I've included a result of Ceva's Theorem in my solution at the bottom.
But this is not CEVA'S THEOREM
Log in to reply
So what should we call this?
Log in to reply
In Korea, this is called angle-ceva's theorem. 각 체바의 정리
https://ko.m.wikipedia.org/wiki/%EA%B0%81%EC%B2%B4%EB%B0%94_%EC%A0%95%EB%A6%AC
Probably something else; but I tried to solve using transformation Geometry which to my surprise didn't work
Log in to reply
@Ariijit Dey – This is Ceva's theorem, because the proof of Ceva's theorem comes from the fact that each the triangles with points that are collinear divided over each other is equivalent to the ones divided over each other on the other side of point P
Excellent Solution by the way
x = 7 1 5 0
Note: Please check Albert Lau's proof using a 42-gon, based on concurrency of 3 diagonals
Albert Lau's approach in using n-gon is more general and can be used for other such adventitous quadrilaterals. See his other posted adventitous quadrilateral problems.
Here, another geometric proof will be given. For an arbitrary angle
x
, construct irregular pentagon
A
B
C
D
E
as per the following figure, WITHOUT drawing line
A
D
with the angles
3
0
−
x
inside triangle
Δ
A
E
D
. This can be done in a straightforward way.
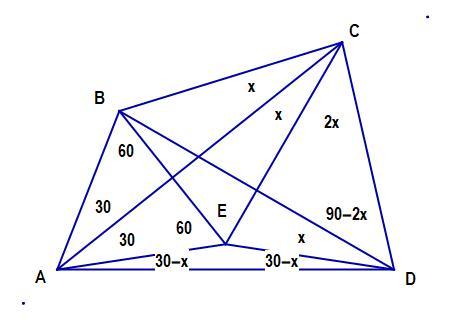
It can be readily seen that when line A D is drawn, triangle Δ A E D is isoceles, and that angles ∠ E A D = ∠ E D A = 3 0 − x . From this, angle ∠ B C A = 6 0 − ∠ C A D
Now, alternatively by trigonometric methods, first, we start with a true equation, and work from there, making use of sum/product of Sines and Cosines
2 ⋅ 2 1 − 1 = 0
2 C o s ( 7 4 2 0 ) − 1 = 0
2 C o s ( 7 4 2 0 ) S i n ( 7 4 8 0 ) − S i n ( 7 4 8 0 ) = 0
S i n ( 7 9 0 0 ) + S i n ( 7 6 0 ) − S i n ( 7 4 8 0 ) = 0
S i n ( 7 9 0 0 ) − 2 C o s ( 7 2 7 0 ) S i n ( 7 2 1 0 ) = 0
S i n ( 7 2 7 0 ) S i n ( 7 9 0 0 ) − 2 S i n ( 7 2 7 0 ) C o s ( 7 2 7 0 ) S i n ( 7 2 1 0 ) = 0
S i n ( 7 2 7 0 ) S i n ( 7 9 0 0 ) − S i n ( 7 5 4 0 ) S i n ( 7 2 1 0 ) = 0
Now refer to the figure below, with more angles put in as easily determined, so that triangle Δ A C D is established, and we let C D = 1 . Then we form another triangle Δ A B C ′ such that ∠ A B C ′ = ∠ C A D + 9 0 , and B C ′ = 1 . We don't know if B C ′ actually meets at vertex C , but we shall find out.
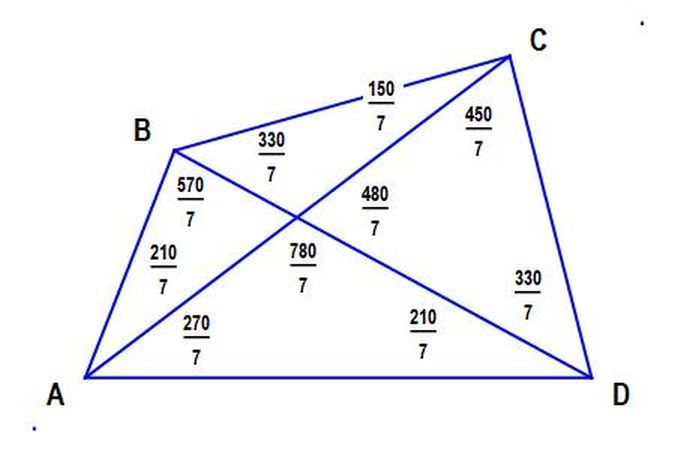
We then determine the length of A C , A C ′ of each, using Law of Sines.
S i n ( 7 2 1 0 ) 1 = S i n ( 7 9 0 0 ) A C
S i n ( 7 2 7 0 ) 1 = S i n ( 7 5 4 0 ) A C ′
From the equation derived from above, we see that A C = A C ′ , and from there we can determine that ∠ B C A = 7 1 5 0 . And once it is seen that Δ B C D is isoceles, we can draw line B D back again with all angles intact.
See
Sum-to-Product Identities
See
Product-to-Sum Identities
For any θ (here in this problem θ = 7 2 7 0 ), the following are true for some L
S i n ( 3 0 ) 1 = S i n ( θ + 9 0 ) L
S i n ( θ ) 1 = S i n ( 2 θ ) L
since if
2 = C o s ( θ ) L
then
S i n ( θ ) 1 = 2 S i n ( θ ) C o s ( θ ) L = S i n ( 2 θ ) L
For a less trivial example which doesn't make use of this identity, check this out
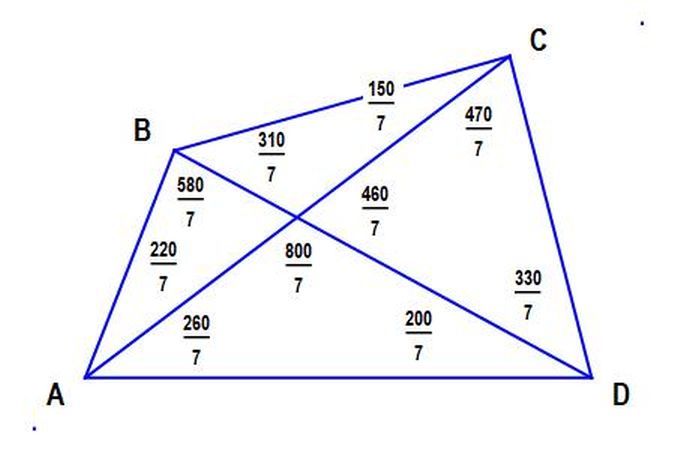
If angles a , b , c , d at the bottom of the quadrilateral are known, then
x = A r c C o t ( S i n ( a ) S i n ( c ) S i n ( b + c + d ) S i n ( a + b + c ) S i n ( c + d ) − C o t ( a ) )
a
=
∠
B
A
C
b
=
∠
C
A
D
c
=
∠
A
D
B
d
=
∠
B
D
C
x
=
∠
B
C
A
If a , b , c , d are all rational angles, and x turns out to be rational also, then all angles in the quadrilateral are rational.
Alternatively (per Ceva's Theorem, thanks Dong kwan Yoo),
S i n ( x ) S i n ( d ) S i n ( a + b ) − S i n ( a ) S i n ( c ) S i n ( b + c + d − x ) = 0
or
S
i
n
(
a
+
b
+
d
+
x
)
+
S
i
n
(
a
+
b
−
d
−
x
)
+
S
i
n
(
a
−
b
−
d
+
x
)
+
S
i
n
(
−
a
−
b
+
d
−
x
)
+
S
i
n
(
−
a
+
b
+
2
c
+
d
−
x
)
+
S
i
n
(
−
a
−
b
−
2
c
−
d
+
x
)
=
0
The Question: For any quadrilateral with all rational angles, is it always possible to resolve this equation, through repeated application of Sum-to-Product and Product-to-Sum identities?
You got to give more details than just the final answer.
I got a formula very much like yours for x but with different angles, but it was too daunting so I just plugged it into my calculator. Then I confirmed with Geometer's sketchpad.
Log in to reply
I've included "a" formula for the benefit of readers that want to check the answer. Many different formulas are possible, it's a question of which looks the tidiest or prettiest.
The interesting question is, which cases yield all rational angles, and why? Sometimes, as with this problem, one can generate such a "rational angle quadrilateral" just by varying one of the angles, which affects the others by some algebraic relation, but other cases are not so simple.
Did you know that there exist a proof WITHOUT trigonometry?
Log in to reply
I think anytime a quadrilateral has all rational angles, there exists a geometrical proof without resorting to trigonometry, even though for some cases, it can be pretty involved. For this problem, it would depend on those angles that are 30 degrees. Can you offer one?
I wasted half an afternoon before turning to trigonometry and solving it in 5 minutes. But it hurts. Please help us out :)
I feel deeply interested in that... Please provide one. Thanks....
My answer is 2795/56.
Your proof needs editing a bit: "Arbitrarily setting /_CBD = 330/7" - Do you mean something like 1) Drawing a line from B to CD (subtending an angle of 330/7), meeting at arbitrary point C' to form a isosceles triangle? Or 2) Drawing a line of length CD from B (subtending 330/7), that ends at an arbitrary point in space C' ?
"Let CD=BD=1" - I suppose you mean something like 1) Let C'D=BC'=1 ? Or 2) Let CD=BC' ?
OR do you mean, assume the angles are 330/7 and 150/7, and then show that this is consistent with the sine rule??
Log in to reply
What I am doing is leave triangle Δ A C D alone since that's established, and then create another triangle A B C with angles 3 0 and 7 9 0 0 , and B C = 1 . Then show that A C , A C ′ are the same, and then draw in line B D . One could argue that I'm deciding that ∠ A B C = 7 9 0 0 because I am assuming that ∠ C B D = ∠ C D B , but I can argue that it's because ∠ A B C = ∠ D A C + 9 0 . An Euclidean approach using this argument is possible, but it'd take up quite a bit more space to demonstrate the identity given "for any θ " This identity does depend on the fact that angles ∠ B A C , ∠ B D A are both 3 0 degrees.
Okay, I've made some changes to the solution to reflect the conversation we are having. What is probably unsatisfying (even though correct) proof is that 1) it uses trigonometry extensively, and 2) it depends on having a preternatural hunch about the nature of that triangle Δ B C D , an isosceles triangle, or at least about that angle ∠ A B C = ∠ C A D + 9 0
Log in to reply
Okay, that makes sense. It is a nice proof. I think both ∠ C ′ B D = ∠ C D B and ∠ A B C ′ = ∠ D A C + 9 0 are required for the proof tho, as you do need B C ′ = 1 for the sine rule used.
I also liked the use of multiple sine rules for the general x. In the 2nd case, do you have any nice identities to show x=150/7 from the expression of arccot? Or is that left to the reader.
Log in to reply
@Alex Burgess – Okay, you're opening up a Pandora's box of complexities when you start asking, "what rational angles a , b , c , d will yield a rational angle x ?" That ArcCot formula should give one an idea of how that's not going to be easy to determine. But I believe that whenever all the angles a , b , c , d , x are rational, i.e., where there exists a trigonometric expression containing just Sine and Cosine functions of rational angles that equals 0, there should exist a way to demonstrate it through Euclidean geometry. I suspect that it could become extremely complicated, as with the non-trivial example I gave at the bottom of my solution.
What I've noticed that, for such all-rational angle quadrilaterals, either 1) there exists a linear algebraic relationship between all angles, or 2) there isn't, so that kind of divides these all-rational quadrilaterals into these two classes. In my solution, I gave an example of both.
Here's another way to express the ArcCot equation entirely in Sine and Cosine form
C
o
s
(
x
)
S
i
n
(
a
)
S
i
n
(
a
)
S
i
n
(
c
)
S
i
n
(
b
+
c
+
d
)
−
S
i
n
(
x
)
S
i
n
(
a
)
S
i
n
(
c
+
d
)
S
i
n
(
a
+
b
+
c
)
−
S
i
n
(
x
)
C
o
s
(
a
)
S
i
n
(
a
)
S
i
n
(
c
)
S
i
n
(
b
+
c
+
d
)
)
=
0
Through repeated applications of the Sum-to-Product and Product-to-Sum identities, this equation can be resolved, every step of the way involving rational numbers that are added or subtracted and/or halved.
i solved it in a different way. by method of reflexion. is there any software to draw geometric figures. it is difficult to solve the problems unless we have a proper drawing. which is the best software.
Log in to reply
Try Geometer's Sketchpad , which Mark Hennings likes to use.
Log in to reply
I like Geometer's sketchpad a lot as well. Desmos geometry has the advantage of being free https://www.desmos.com/geometry
Log in to reply
@Jeremy Galvagni – Desmos seems quicker to set up and get going with graphics, I think? I'm looking into it now.
Log in to reply
@Michael Mendrin – Each can do things the other can't. The graphing calculator is the best.
i am sorry. i solved it exactly the way you solved it without using any trigonometry.
Log in to reply
What's to be sorry about? Did you make use of an equilateral triangle somewhere?
Log in to reply
i was in a hurry. my proof is totally different. i took reflexion of B about AC. i get a new triangle B"AD. i will extend AB" so that it meets BD at D". angle CAD"=angle BDA=30. this implies that AC is tangent to the ex-circle of the triangle AD' D. then i draw a line perpendicular to AC passing through A. it is clear that the centre of the excircle of the triangle AD'D lies on this line. after this observation with little effort i could find a cyclic quadrilateral. that finishes the problem.
Log in to reply
@Srikanth Tupurani – my geometry is so poor. it is not ex-circle. it is circumcircle of triangle AD'D. i am really shocked. i missed out that equilateral triangle.
Notice that 2 1 . 4 2 8 5 7 1 4 3 + 3 8 . 5 7 1 4 2 8 5 7 = 6 0
See my geometrical proof at top.
Log in to reply
Interesting.
Don't worry bout it, I did a ton of law of sines bashing and then used a calculator at the end
where from did you get the tool/software? pls give me the link
Log in to reply
Autodesk Autocad. Not really designed for math so it might be better to check geogebra.
Log in to reply
No, I meant Wolfram Mathematica It is quite expansive and I thought you somehow managed to get it free
Log in to reply
@Ariijit Dey – Read the letters in the photo and google it.
amazing software. we can solve every geometry problem using this. synthetic methods require lot of practice. some problems need extremely creative constructions. but it is better to use software than using non-synthetic methods. non-synthetic solutions are lengthy and ugly.
You are fool
Log in to reply
this is too harsh. in real life most of the things are solved by using softwares.
This solution is inspired by Michael Mendrin's solution on a similar problem.
This solution will be attempted without trigonometry as an added challenge.
for simplicity, let u = 7 3 0 ∘ , 4 2 u = 1 8 0 ∘
we start by constructing a regular 42-gon and connect 6 diagonals. any angles on vertices are founded by counting number of subtended sides. the rest can be found by using triangles.
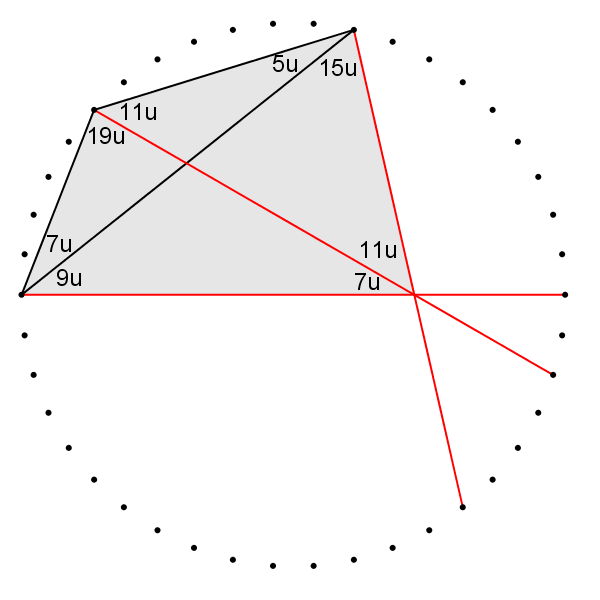 by comparing the angles,
x
=
5
u
=
7
1
5
0
∘
. unfortunately this proof is incomplete without proving concurrency of 3 (red) lines.
by comparing the angles,
x
=
5
u
=
7
1
5
0
∘
. unfortunately this proof is incomplete without proving concurrency of 3 (red) lines.
we will complete the proof by constructing
A
D
,
E
D
, and try to prove
B
C
D
F
is collinear.
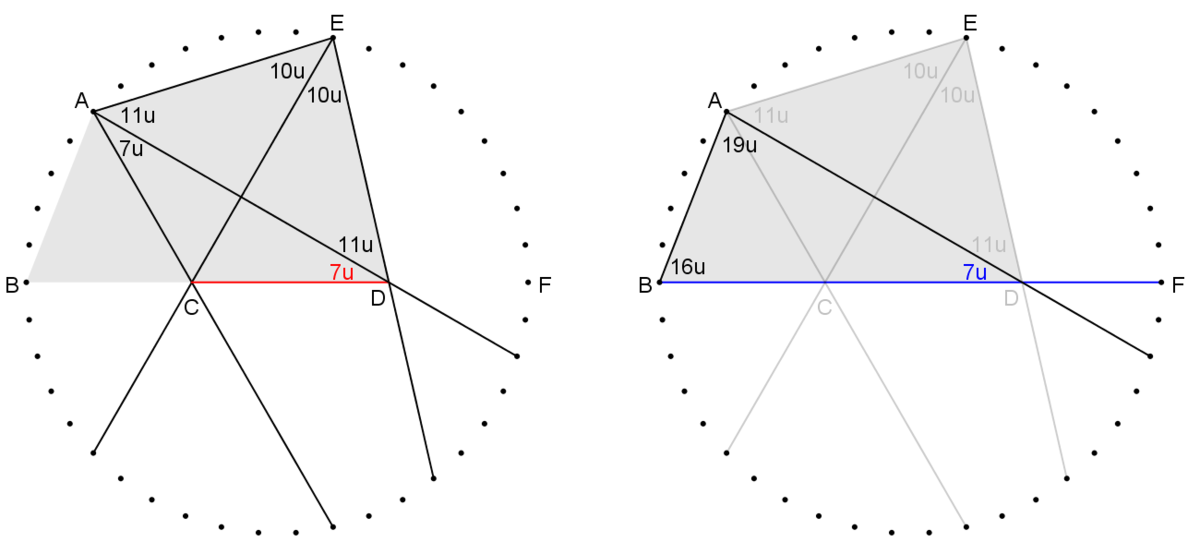 on left diagram, we construct 5 diagonals as shown. connect
C
D
. it can be shown that
A
C
D
E
is a kite, hence
∠
A
D
C
=
7
u
.
on left diagram, we construct 5 diagonals as shown. connect
C
D
. it can be shown that
A
C
D
E
is a kite, hence
∠
A
D
C
=
7
u
.
on right diagram, we construct 3 diagonals as shown. ∠ A D B = 7 u .
since both C D and B D makes the same angle 7 u from A D , then B C D F must be collinear, proving concurrency of lines B F , A D , E D , which completes the proof.
The illustration and proof using the 42-gon is really beautiful, event though the last step is a bit subtle and requires careful thought. (We know how easy it is for me to go wrong with this approach!) One might argue if it's any more elegant than other possible non-trigonometric proofs, but we're investigating if all "adventitous quadrilaterals" can be analyzed by means of such n-gons. I think that for every such adventitous quadrilateral, there is an associated cyclic quadrilateral divided into 3 triangles, all with rational angles, so that proving one proves the other. I'll try to post such a cyclic quadrilateral for this problem here to see if that's any help towards a systematic treatment.
Log in to reply
yes, im figuring some systematic treatment too, my best guess is to use kites, but the 3 kites we've seen are so different from each other. in fact i used geogebra to try fit the shape into different position and see if any kite pop out, its just trial and error.
(though i secretly hope there isnt one, because i have more similar problems which i might post in the future.)
Log in to reply
What I seem to find with "adventitious quadrilaterals" is that some of them have the angles in an algebraic relationship, so that one can vary one angle which produces more of the same. Others do not allow such variation, and are "one-of"s. I look forward to more of your posts on this kind of problem, as this is a deep subject involving different aspects of mathematics.
Here we draw lines
A
D
,
B
E
,
C
F
, and the cyclic quadrilateral
A
B
C
D
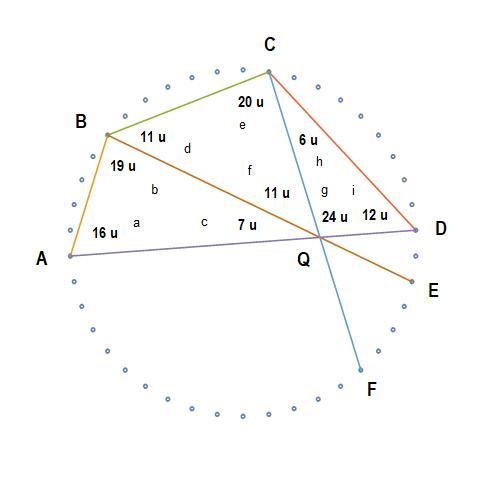 The angles are in units
u
=
7
3
0
degrees, from
a
to
i
, which satisfy the following
The angles are in units
u
=
7
3
0
degrees, from
a
to
i
, which satisfy the following
a
+
b
+
c
=
4
2
u
d
+
e
+
f
=
4
2
u
g
+
h
+
i
=
4
2
u
a
+
e
+
h
=
4
2
u
b
+
d
+
i
=
4
2
u
Given angles b = 1 9 u , d = 1 1 u , e = 2 0 u , h = 6 u , all the other angles are uniquely determined. But do the vertices of this cyclic quadrilateral necessarily lie on the vertices of the 42-gon? Hmm..., no, not necessarily. Oh well .
Log in to reply
given b,d,e,h, not all the other angles are uniquely determined. line AD can be "rotated" about Q which makes line AD cuts the other two sides outside the circle.
fixing a=16u will fix the whole diagram, and will give a+e+h=42u which proves it to be cyclic.
Log in to reply
I'm still thinking about this angle, pun or no pun. I don't know if this cyclic quadrilateral makes this any easier.
Log in to reply
@Michael Mendrin – i'd say the whole n-gon method definitely not easier. behind this seemingly elegant solution is hours to days of trial and error using computer softwares, without geogebra i'd never make it. but its fun to know there's a connection.
Log in to reply
@Albert Yiyi – Yeah, agree... so much for finding the "Rosetta Stone" of adventitous quadrilaterals.
Just think of two same base triangle ABC and DBC with common base BC.
in triangle ABC,
angle ABC=30+270/7,
angle ACB=30 and angle BAC=180-(ABC+ACB).
In triangle DBC,
angle DBC=270/7,
angle DCB=30+330/7,
angle BDC=180-(DBC+DCB).
Suppose BC=1 unit, then try to find AC and CD,
You know the angle ACD ,
now it is easy for you to find angle ADC from triangle ADC.
Then find ADC-BDC
You will find ADB which is 150/7
Can you please elaborate on "now it is easy for you to find angle ADC from triangle ADC". To me it seems anythings but easy, though I might be overlooking something. Both angles CAD=30+270/7-x, ADC=x, and also AD are unknown. Sine rule will lead to a mess. One can find answer numerically (which I did), but finding it exactly seems to me quite elaborate.
B A C = 7 5 7 0
B D C = 7 4 5 0
Let BC = 1
Apply sine rule s i n 3 0 A B = s i n 5 7 0 / 7 1
AB = 0.506
Apply sine rule s i n 5 4 0 / 7 B D = s i n 4 5 0 / 7 1
BD = 1.082
Apply cosine rule A D 2 = ( 0 . 5 0 6 ) 2 + ( 1 . 0 8 2 ) 2 − ( 2 × 0 . 5 0 6 × 1 . 0 8 2 × c o s 3 0 )
AD = 0.692
Apply sine rule s i n x 0 . 5 0 6 = s i n 3 0 0 . 6 9 2
Sin x = 0.365
X = 7 1 5 0
x = 7 1 5 0
We can solve this problem by using slopes.
First notice that in order to make a line have a certain angle from the x axis, you make the tangent of the desired angle the slope. For example:
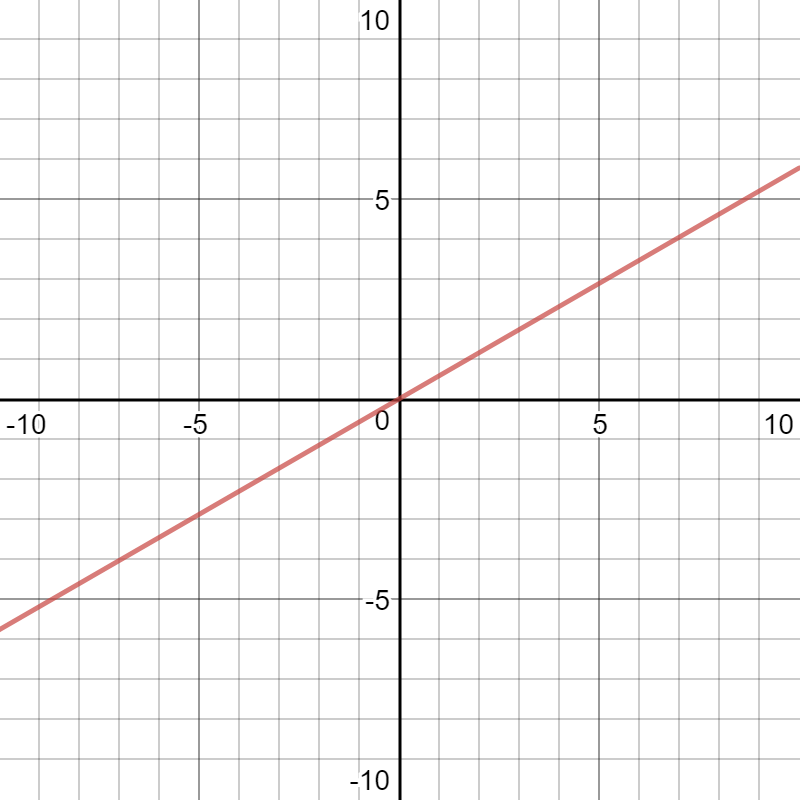
We can model this figure with equations using this technique:
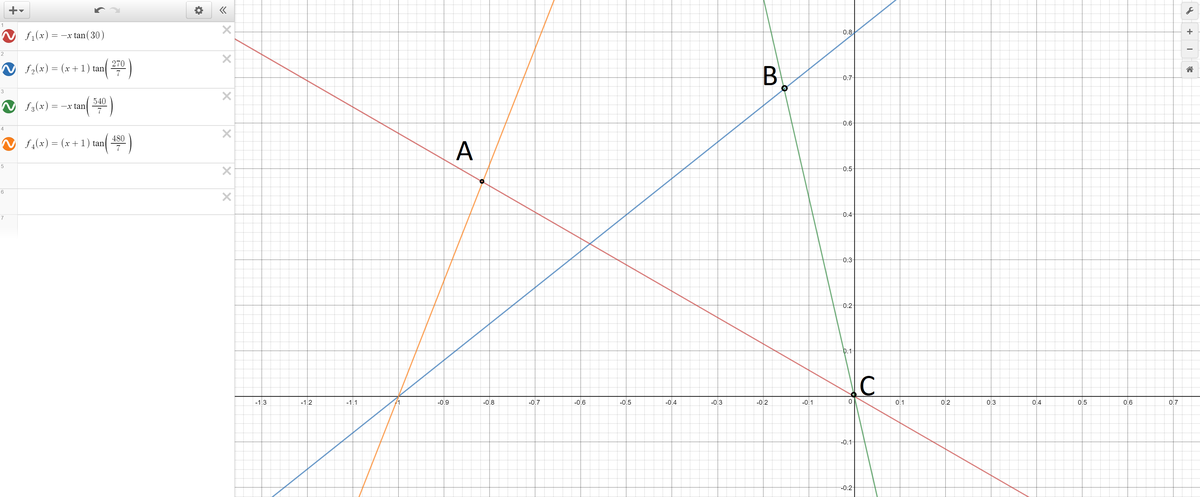
We can then find the slope between A and B, which after a lot of ugly algebra is equal to tan(120/7). The other "half" of angle A is 30 degrees, which can be found from the slope between point A and the origin.
Angle A = 330/7
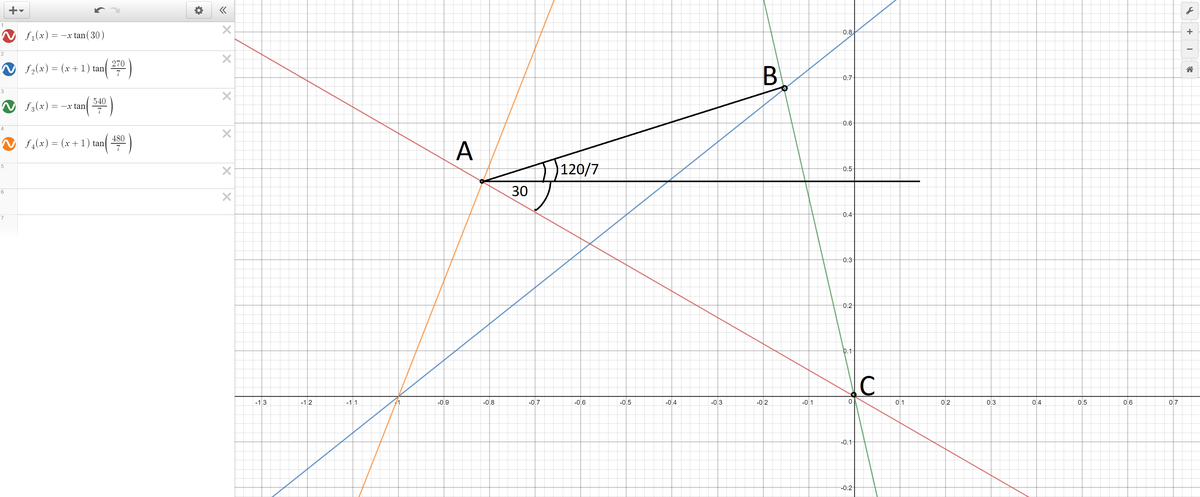
Adding these two angles yields (\frac{330}{7}) degrees for angle A.
The sum of all interior angles except for X and A can be found through some finagling of angles, and turns out to be 7 2 0 4 0 . Since the inside angles of a quadrilateral add up to 360:
2040/7 + A + X = 360
A + X = 480/7
330/7 + X = 480/7
X = 150/7