What's the Altitude?
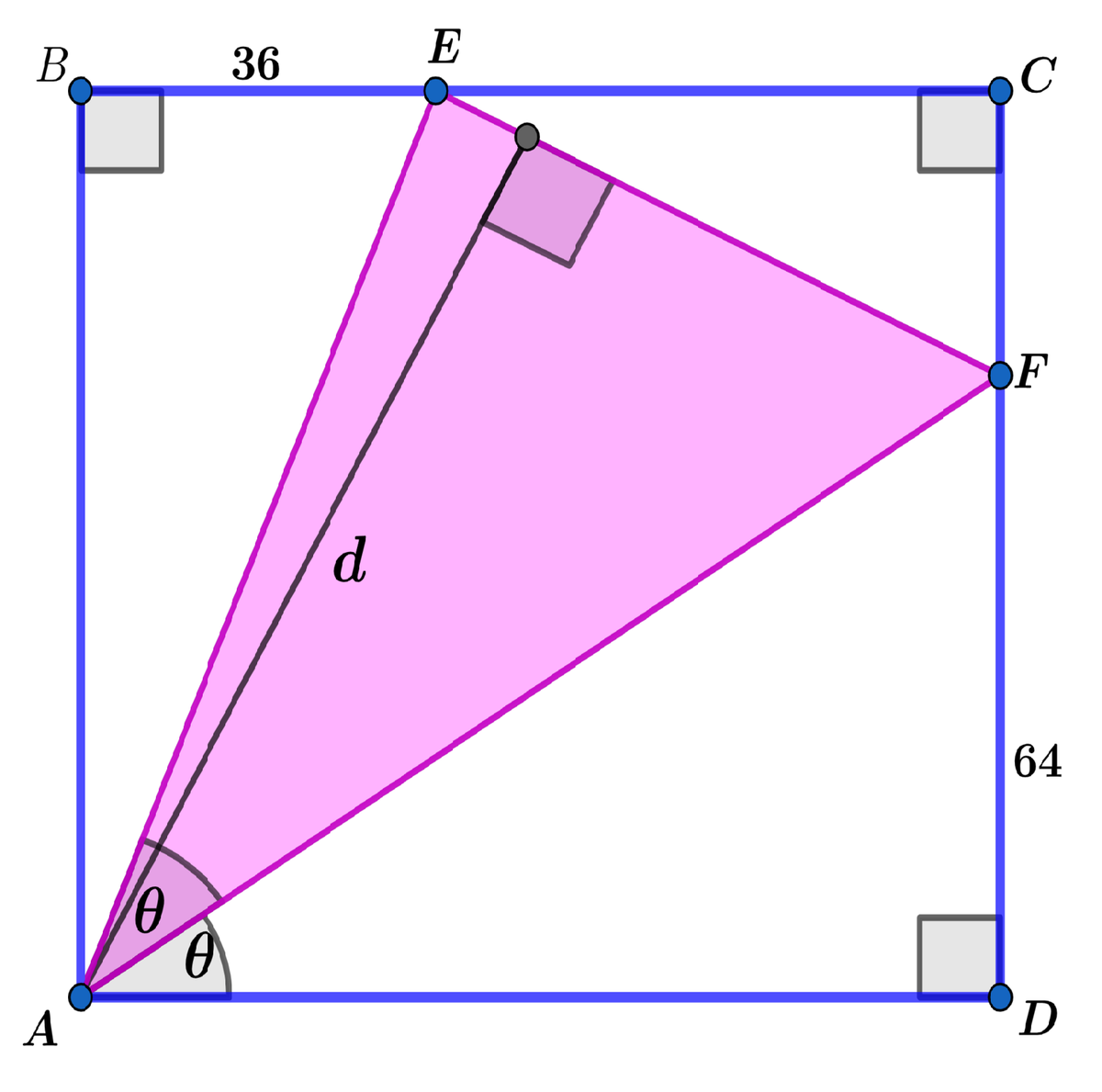
In square A B C D , A F bisects ∠ E A D , B E = 3 6 , and D F = 6 4 . If the altitude of △ A E F can be represented by
d = b − c d ∗ a
where a , b , c , and d ∗ are coprime positive integers, find a + b + c + d ∗ .
The answer is 419.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Area of △ A E F is 3 2 0 0 . Length of side E F is ( 3 6 − 8 7 0 4 ) 2 + ( 8 7 0 4 − 6 4 ) 2 = 2 0 5 7 − 8 3 4 . So the altitude is given by d = 5 7 − 8 3 4 3 2 0 . Therefore, a = 3 2 0 , b = 5 7 , c = 8 , d = 3 4 and a + b + c + d = 4 1 9
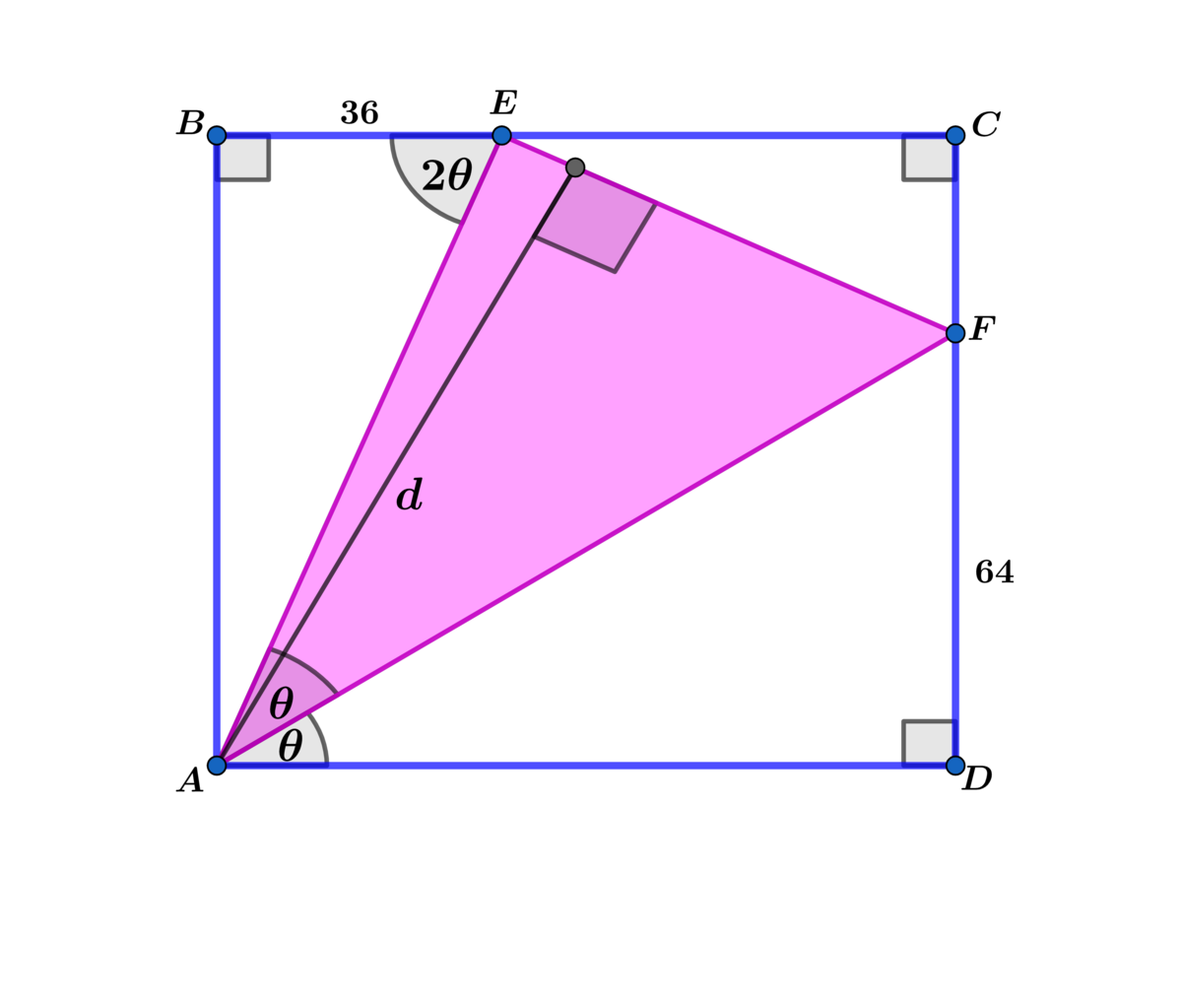
In square A B C D let A B = x ⟹
A E = x 2 + 3 6 2 , A F = x 2 + 6 4 2 and sin ( 2 θ ) = x 2 + 3 6 2 x = 2 sin ( θ ) cos ( θ ) , where sin ( θ ) = x 2 + 6 4 2 6 4
and cos ( θ ) = x 2 + 6 4 2 x
⟹ sin ( 2 θ ) = x 2 = 3 6 2 x = 2 sin ( θ ) cos ( θ ) = x 2 + 6 4 2 1 2 8 x
⟹ 1 2 8 x 2 + 3 6 2 = x 2 + 6 4 2 ⟹ x 4 − 2 ∗ 6 4 2 x 2 − 6 4 2 ∗ 8 2 ∗ 1 7 = 0
⟹ x 2 = 4 0 9 6 ± 4 6 0 8
Choosing the positive real root ⟹ x = 8 7 0 4 = 1 6 3 4
To find the distance d :

U = ( 8 7 0 4 − 3 6 ) i + ( 6 4 − 8 7 0 4 ) j + 0 k
V = 8 7 0 4 i + 6 4 j + 0 k
⟹ ∣ U X V ∣ = ∣ 6 4 8 7 0 4 − 2 3 0 4 − 6 4 8 7 0 4 + 8 7 0 4 ∣ = 6 4 0 0
and U = 4 ( 4 3 4 − 9 ) 2 + ( 1 6 − 4 3 4 ) 2 = 2 0 5 7 − 8 3 4
⟹ d = 5 7 − 8 3 4 3 2 0 = b − c d ∗ a ⟹ a + b + c + d ∗ = 4 1 9 .
@Rocco Dalto , you have used d on both sides of the equation d = b − c d a , but they are of different values.
@Rocco Dalto Do you any recommendation for some book on 3D geometry or nD geometry, I am not used to with it... I like the questions that you give on 3D geometry but I do not have any clue how to do it.
Log in to reply
I have my college math textbooks, but they were from the early 80's. haven't been to a bookstore in forty years. I recommend looking for a textbook on vector calculus and possibly linear algebra. You could also look online for 3d geometry. You could also play around with geogebra 3D.
Log in to reply
Thank you very much.
Let the side length of square A B C D be a . Then tan θ = a 6 4 and
tan ( 9 0 ∘ − 2 θ ) 2 tan θ 1 − tan 2 θ 2 × a 6 4 1 − ( a 6 4 ) 2 1 − a 2 6 4 2 ⟹ a 2 a = cot 2 θ = tan 2 θ 1 = a 3 6 = a 3 6 = a 3 6 = a 2 2 × 6 4 × 3 6 = 8 7 0 4 = 1 6 3 4
The area of △ A E F :
[ A E F ] = a 2 − ( 2 6 4 a + 2 3 6 a + 2 ( a − 6 4 ) ( a − 3 6 ) ) = a 2 − ( 2 a 2 + 1 1 5 2 ) = 2 a 2 − 1 1 5 2 = 2 8 7 0 4 − 1 1 5 2 = 3 2 0 0
The length of E F is ( a − 6 4 ) 2 + ( a − 3 6 ) 2 = 2 0 5 7 − 8 3 4 and the altitude of △ A E F , d = 2 0 5 7 − 8 3 4 3 2 0 0 × 2 = 5 7 − 8 3 4 3 2 0 . Therefore, a + b + c + d ∗ = 3 2 0 + 5 7 + 8 + 3 4 = 4 1 9 .