What's the area of this rectangle?
Given the areas of the triangles, find the area of this rectangle.
The answer is 336.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Wonderful solution with Menelaus's Theorem. Very well done!
Fantastic! However, you should precise which triangle and secant you used and how you can use area ratios.
Learn something new everyday. It took me a while to see how you used Menelaus' Theorem, but appreciate that no midpoint assumption was needed for central triangle. It turns out it is in the middle, but you showed it's not necessary to assume this. Well done.
Very nice but could you explain how the bottom equation results from Menelaus' theorem. I got a similar equation from using the theorem on the right hand 21 triangle. The equation I got was: [(21+x)/x ] [(3y+x+6)/(3y+6)] [3y/(3y+x+21)]=1. The result is the same but the equation above is simpler
Log in to reply
I got my equation by using the Menelaus' Theorem on the central triangle (the triangle containing three parts: a 21-triangle, an x-triangle and a 3y-triangle), and the secant which devides this triangle into 21 and x+3y.
Log in to reply
Thanks a lot but I still can't see it. Which is the line which the extended sides of the triangle are on? (I am referring to the Menelaus theorem that talks about extending sides of a triangle that meet the same line. Perhaps you are referring to some variation of this theorem?) Thanks
Ok. Got it.Thanks. (Please disregard my previous comment)
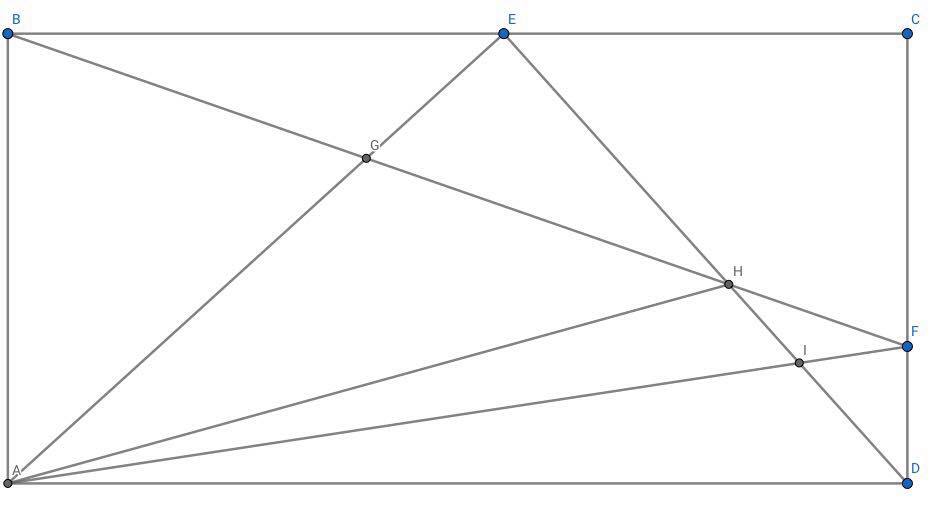 Since
Δ
B
E
G
=
Δ
H
E
G
=
2
1
and both traingles have the same height, then
B
G
=
G
H
Since
Δ
B
E
G
=
Δ
H
E
G
=
2
1
and both traingles have the same height, then
B
G
=
G
H
We can deduce that Δ B A G = Δ H A G since they have the same height.
Let Δ B A G = Δ H A G = a .
Also Δ H F I = 6 ; Δ D F I = 8 and both traingles have the same height, then I D H I = 8 6 = 4 3
We can deduce that Δ A H I = 3 b ; Δ A D I = 4 b for some positive number b .
Note that Δ A E D = 2 1 A B C D = Δ B F A
⟹ 2 a + 3 b + 6 = a + 7 b + 2 1
⟹ a = 4 b + 1 5
Also notice that Δ C B F + Δ D A F = Δ A E D
⟹ Δ B E H + E C F H + Δ D A F = Δ A E D
⟹ 4 2 + E C F H + 4 b + 8 = 4 b + 1 5 + 7 b + 2 1
⟹ E C F H = 7 b − 1 4
⟹ A B C D = 2 2 b + 7 2
Since E is the midpoint, Let A B = x , B C = y , B E = 2 y
⟹ x y = A B C D = 1 6 b + 1 4 4
⟹ b = 1 2
∴ 2 2 ( 1 2 ) + 7 2 = 3 3 6
I based the fact that E is the midpoint on the diagram. If you can find a way to show that no matter where E is the condition will still be true, then please share it.
Log in to reply
I guess the solution using Menelaus' Theorem comes closest. For the numbers given E is the midpoint, but apparently this assumption is not necessary. That said, I couldn't get the answer.
Log in to reply
Actually it can be shown that A E / / C H and since B G = G H , we can conclude that B E = E C . Although I guess my solution would be longer.
I'm not too sure how it went from xy=ABCD=16b+144 to b=12. Can you elaborate what exactly happened there?
Log in to reply
Note that Δ A B E = 4 x y = 4 b + 3 6
⟹ x y = 1 6 b + 1 4 4
Now equate it to x y = 2 2 b + 7 2 = 1 6 b + 1 4 4
⟹ b = 1 2
Thanks for pointing it out to me.
Hans, I liked your solution very much and I was able to understand most of it. However I have a few doubts as follows; 1--> You made a statement that both triangles BEG and HEG have the same height. As a result, triangles BAG and HAG have the same height, which makes BAG and HAG with the same area. Can you elaborate on that? 2--> You applied the same analogy for triangles HFI and DFI, resulting that triangles AHI and ADI have the proportional areas of 3/4. Can you elaborate on that as well? 3 --> I was also not able to counteract on the assumption you made that point E is the midpoint of segment BC.
By applying a horizontal scale of factor λ , coupled with a vertical scale of factor λ − 1 , we can retain the areas of the various regions, but have the whole problem inside a square.
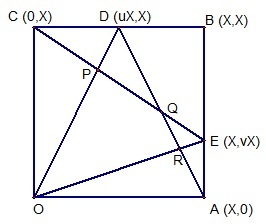
Assume then that the points A , B , C have coordinates ( X , 0 ) , ( X , X ) and ( 0 , X ) respectively, and that the points D , E have coordinates ( u X , X ) and ( X , v X ) for some 0 < u , v < 1 . Then the points P , Q , R have coordinates ( 1 + u − u v u X , 1 + u − u v X ) ( u + v − u v u X , u + v − u v v X ) ( 1 + v − u v X , 1 + v − u v v X ) respectively (these are found by solving suitable pairs of simultaneous equations).
Thus we have triangle areas: 2 1 = 2 1 × u X × 1 + u − u v u ( 1 − v ) X = 2 ( 1 + u − u v ) u 2 ( 1 − v ) X 2 2 1 + 2 1 = 2 1 × u X × u + v − u v u ( 1 − v ) X = 2 ( u + v − u v ) u 2 ( 1 − v ) X 2 and these equations tell us that 1 + u − u v = 2 ( u + v − u v ) ⇔ v = 2 − u 1 − u We also have the triangle areas: 6 + 8 = 2 1 × v X × u + v − u v ( 1 − u ) v X = 2 ( u + v − u v ) ( 1 − u ) v 2 X 2 8 = 2 1 × v X × 1 + v − u v ( 1 − u ) v X = 2 ( 1 + v − u v ) ( 1 − u ) v 2 X 2 and so 4 ( 1 + v − u v ) = 7 ( u + v − u v ) ⇔ v = 3 ( 1 − u ) 4 − 7 u Thus we deduce that 2 − u 1 − u = 3 ( 1 − u ) 4 − 7 u , which implies that u = 2 1 or 2 5 . Since 0 < u < 1 we deduce that u = 2 1 , and hence v = 3 1 . We then obtain the area equations 2 1 = 1 6 1 X 2 6 = 5 6 1 X 2 8 = 4 2 1 X 2 and hence we see that all is well, and that the area of the rectangle is X 2 = 3 3 6 .
Can you explain how you associate the rectangle with the square? Also how did you get to the points P, Q, R coordinates?
Log in to reply
If I scale U × V rectangle with a horizontal scale factor of U V , and also with a vertical scale factor of V U , I end up with a U V × U V square. Straight lines will be mapped to straight lines, and areas will be unchanged.
To find P , for example, I solve the simultaneous equations u y = x y = X − ( 1 − v ) x Similar pairs of equations can be found to determine Q and R .
@Mark Hennings This technique seems pretty good! Where could I find more info of scaling like this?
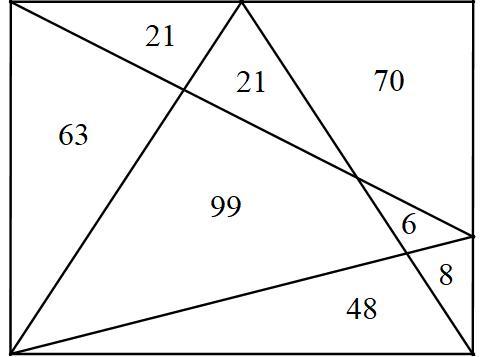
Apex of upright triangle is at midpoint of top. Apex of other triangle is 3 1 of the height.
For sake of ease of computations, assume height = 2 1 , width = 1 6 , but any rectangle of area 3 3 6 will work.
how can you judge the upright point is the midpoint? Kind of guess?
How many such rectangles can be generated with these perimeters, that the areas of those 4 triangles are 21,21,8,6?
Easy to see:
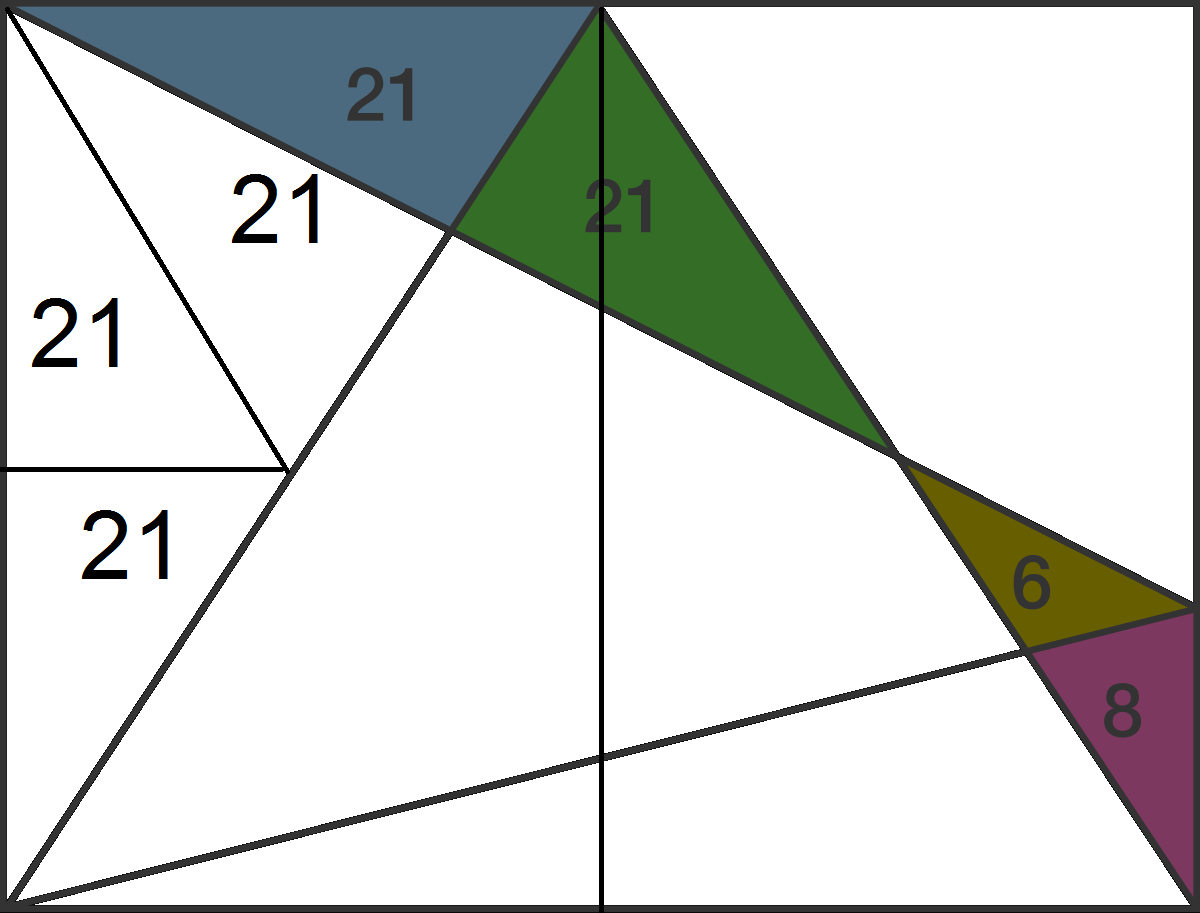
Area = 21 x 4 x 4 = 336
Okay, this is an unusual solution, because it makes a number of unexplained assumptions. Not quite so easy to see. How do you know that both the blue and green triangles are right triangles? But since the rectangle can have any dimensions provided that its area is 336, then it's possible to find one where the blue and green triangles are both right triangles. But even given that, that doens't establish that the vertex the blue and green triangles share is 3/4 of the height of the rectangle, which is what's needed to show that the white triangle has an area of 63.
This is all you need if you assume G is the midpoint of the top.
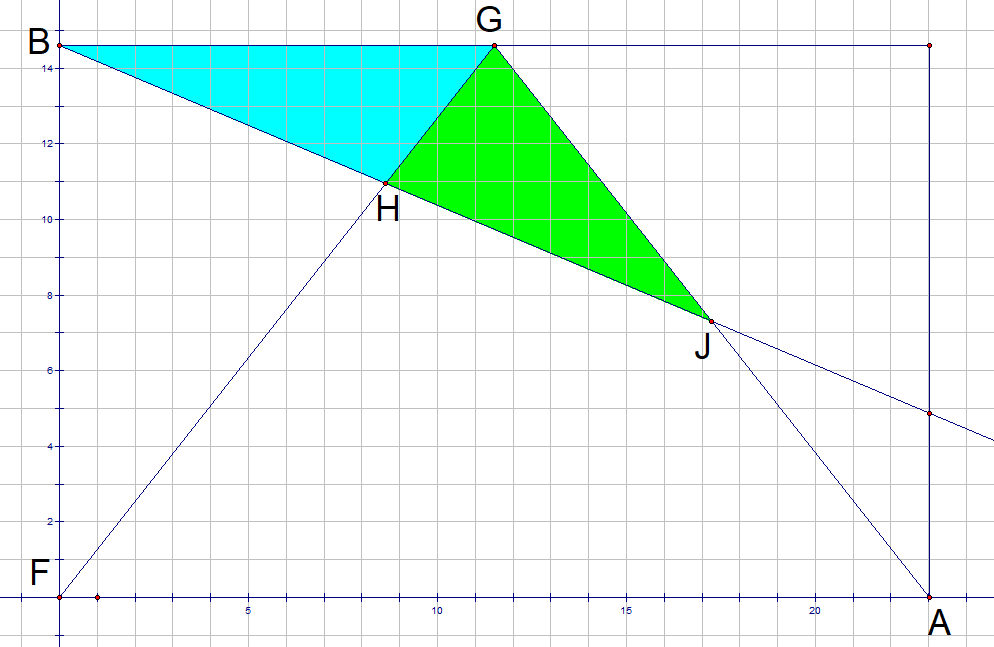
B=(0,b), A=(a,0), the area of the rectangle sought is ab.
Line FG is y = a 2 b x , line GA is y = a − 2 b x + 2 b
Since BG = a/2 to make the area of triangle BHG be 21, its height must be 84/a and so the y-coordinate of H is b-84/a
H = ( 2 a − b 4 2 , b − a 8 4 )
Since triangle GHJ also has area 21, BJ=2*BH
J = ( a − b 8 4 , b − a 1 6 8 )
This point must lie on GA. Substituting into the equation for this line gives
b − a 1 6 8 = a − 2 b ( a − b 8 4 ) + 2 b
b = a 3 3 6
a b = 3 3 6
How do you know BG =a/2? It may be, but I think it can be solved without this assumption. The only problem is that it appears to be a nonlinear equations nightmare. I noticed everyone assumed apex at the midpoint..
Log in to reply
I don't think the other solutions assume this BG=a/2. Some prove it, other's don't need it. I was just pointing out that with the assumption you don't need to know about the little triangles with areas 6 and 8.
Let a and b be the length and width of the rectangle, such that b = x * a ==> S0 = a * b = x * a ^ 2. In an orthonormal reference of origin O (0,0), the different points have coordinates: A (0, x * a); B (y * a, x * a); C (a, x * a); D (a, x * t * a); E (a, 0) with 0 <x, y, t <1.It is necessary to calculate the equations of the different lines passing through these points in accordance with the statement.Thus, we will determine the coordinates of the 3 internal points of intersection.After calculation, F (y * a / (1-y * t + y), xa / (1-y * t + y)); G (y * a / (t-y * t + y), x * t * a / (t-y * t + y)); H (a / (1-y * t + y), x * t * a / (1-y * t + y)) The triangles (A, B, F) and (A, B, G) have the following meanings: base [AB] = y * a and respective heights [x * a-xa / (1-y * t + y)] and [x * a- x * t * a / (ty * t + y)]. Which is translated in other words by: 21 = S (A, B, F) and 21 + 21 = S (A, B, G). And the other 2 known triangles S (D, E, G) = 14 and S (D, E, H) = 8 are based on [DE] and for respective heights [ay * a / (ty * t + y)] and [a- a / (1-y * t + y) After solving the system of equations, we get: y = 1/2; t = 1/3 and (x * a ^ 2) / 24 = S0 / 24 = 14 or (x * a ^ 2) / 42 = S0 / 42 = 8 ===> S0 = 336
Relevant wiki: Menelaus' Theorem
Solve this quadratic equation and we get x=63, y=12, S=336.
Wikipedia for Menelaus's Theorem