When the circle leads to the square
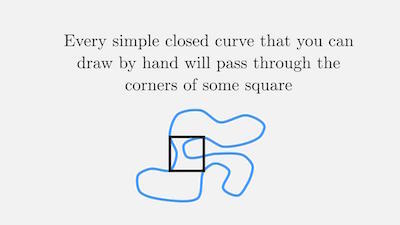 This problem is inspired by a Fermat's Library tweet: https://twitter.com/fermatslibrary/status/1099301103236247554
This problem is inspired by a Fermat's Library tweet: https://twitter.com/fermatslibrary/status/1099301103236247554
Find the perimeter of the square the corners of which are shared by the ellipses 3 x 2 + 3 x y + 7 y 2 − 1 2 x − 6 y − 1 3 = 0 and 1 1 x 2 − 6 x y + 3 y 2 − 4 4 x + 1 2 y + 9 = 0 .
The answer is 12.649.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

If you notice, both ellipses pass through the points ( 1 , 2 ) , ( 4 , 1 ) , ( 3 , − 2 ) , ( 0 , − 1 ) . This forms a square with side length 1 0 (because each square side is the hypotenuse of a triangle with sides 1 and 3 , and so using Pythagorean Theorem, we have 1 2 + 3 2 = 1 0 ). So the perimeter is 4 × 1 0 = 1 2 . 6 4 9 .
@Joshua Lowrance , how did you plot the graph?
Log in to reply
I used Desmos.com
Log in to reply
Thank you!
Used Desmos.com just as you.
Multiply the first equation by 2 and add it to the second to obtain 1 7 x 2 + 1 7 y 2 − 6 8 x − 1 7 = 0 .
This is the equation of a circle with center at ( 2 , 0 ) and radius r = 5 , as we can see by doing the following transformations:
Divide by 1 7 : x 2 + y 2 − 4 x − 1 = 0
Build a perfect square with the terms that contain x : x 2 − 4 x + 4 + y 2 − 4 − 1 = 0 ⟹ ( x − 2 ) 2 + y 2 = 5 .
The square we are looking for must be inscribed in this circle and its side is l = 2 r = 1 0 . The perimeter is therefore 4 1 0 ≈ 1 2 . 6 5 .
This is a nice way of answering the question without having to find the four vertices of the square, which are ( 0 , − 1 ) , ( 1 , 2 ) , ( 4 , 1 ) and ( 3 , − 2 ) .