When two lines meet!!

Algebra Level 4

Find the number of roots of equation $f(x) =|\log_{10}(x-6)| - |e^\frac 1x + 2|$ .

All of my problems are original

Difficulty: $\dagger \dagger \dagger \color{grey}{}\dagger \color{grey}{\dagger}$

1 7 2 0 4 3 5 6

Aryan Sanghi
May 7, 2020

f(x) =|log(x-6)| - |e $^\frac{1}{x}$ + 2| = 0

|log(x-6)| = |e $^\frac{1}{x}$ + 2|

So, we have to basically find points of intersection of y = |log(x-6)| and y = |e $^\frac{1}{x}$ + 2|

Here is the graph

So, we can see that they intersect at two points. So, there are 2 roots

Wait a sec, how come I got this?! :D

Jeff Giff - 11 months, 2 weeks ago

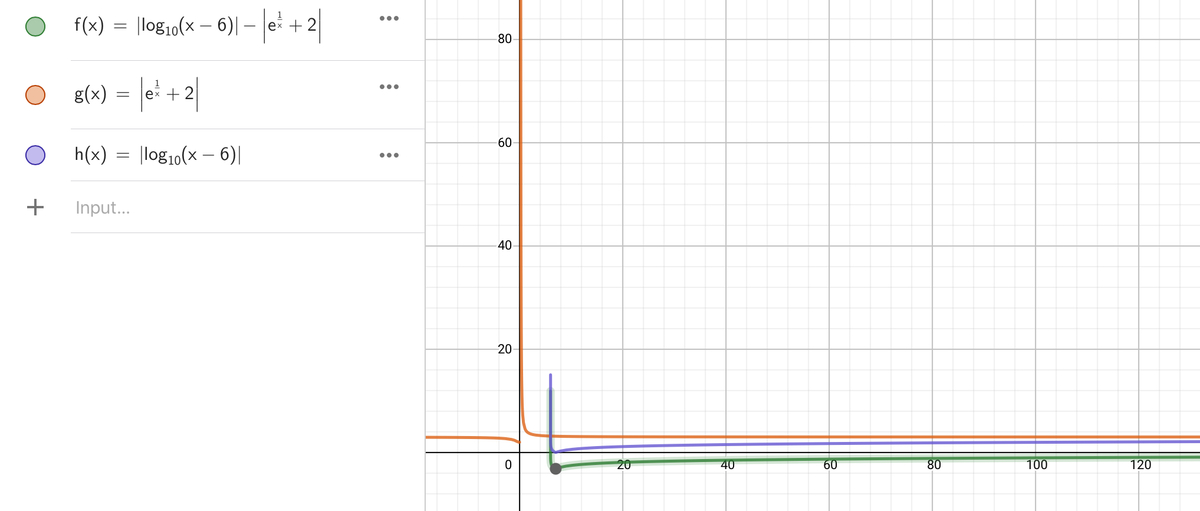
Above graph also has 2 solutions only.

Aryan Sanghi - 11 months, 2 weeks ago

I don’t see the second?

Jeff Giff - 11 months, 2 weeks ago

@Jeff Giff – It's very far, at $x = 10^8$ maybe.

Aryan Sanghi - 11 months, 2 weeks ago

@Aryan Sanghi – Oh my god, I got $1000\leq x\leq 1100$ , but didn’t see it on my graph :P

Jeff Giff - 11 months, 2 weeks ago

Because normally, we assume $\log x=\log_{10} x.$

Jeff Giff - 11 months, 2 weeks ago

I also assumed the same, base 10.

Aryan Sanghi - 11 months, 2 weeks ago