Where Are The Alternate Angles?
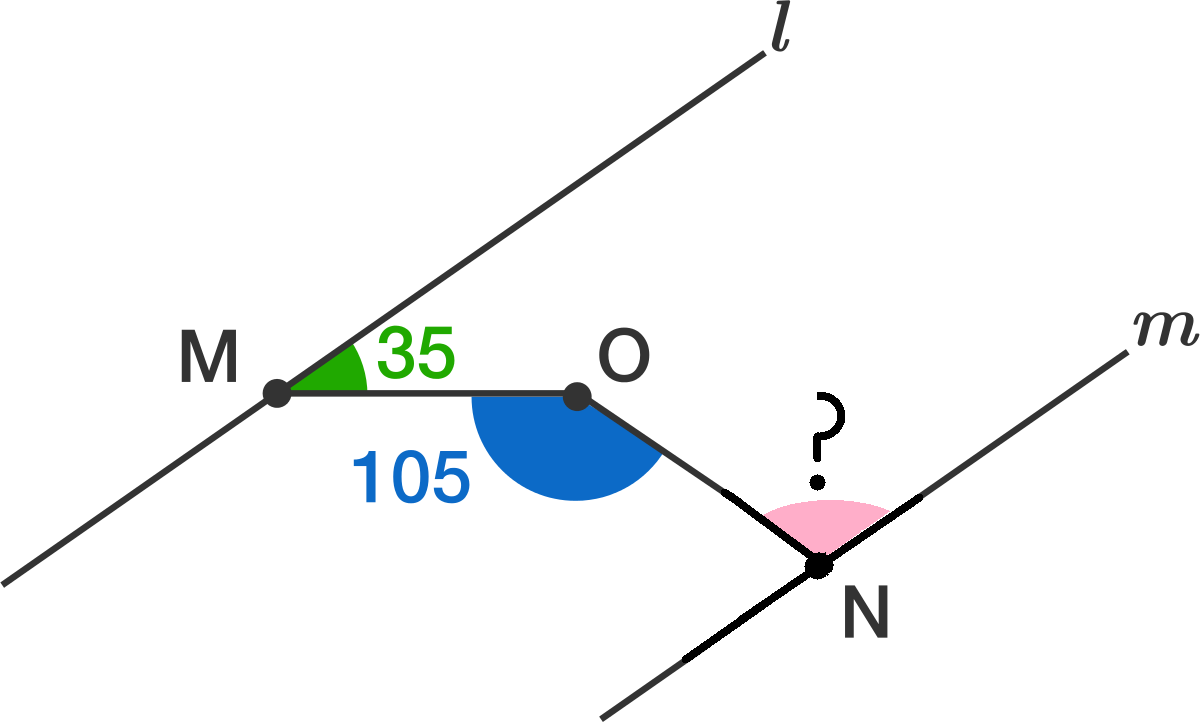
Lines l and m are parallel. M , N and O are points such that M is on l and N is on m and O is between the two lines. If the smaller angle between l and M O is 3 5 ∘ and ∠ M O N = 1 0 5 ∘ , find the acute angle between m and N O .
Clarification: The diagram is not accurate
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Where is point D? Let the line NO be extended to line l such that it meets line l at point P. If <NOM = 105, hence < MOP = 75. If <MOP and <OMP are 75 and 35 degrees respectively, the <MPO = 70. If <MPO= 70, then the pink angle is 180-70 = 110.
Log in to reply
Yes, the pink angle in the diagram is 1 1 0 ° , but the question asks for the acute angle between m and N O .
Thus, 1 8 0 ° − 1 1 0 ° = 7 0 ° .
The problem has been edited before it had a point D.
tsk its 110... the angle inside triangle MNQ is 70,75,and 35,,,and the supplement of 70 is 110
Log in to reply
Note the question asks for the acute angle.
Log in to reply
yap but in the diagram the pink angle must be 110. by the way thank you mam.. =)
Log in to reply
@Reygan Dionisio – Why do you keep looking at the diagram? The question asks for the acute angle. Are you saying that 1 1 0 ° is acute?
I didnt put the image up. Staff must have done so. Sorry about the misleading diagram.
Log in to reply
Sorry about that. I have removed the image.
In future, please let me know if you notice such errors, and I can correct for them.
First extend ∠ M O N and as well as the components of ∠ l M O
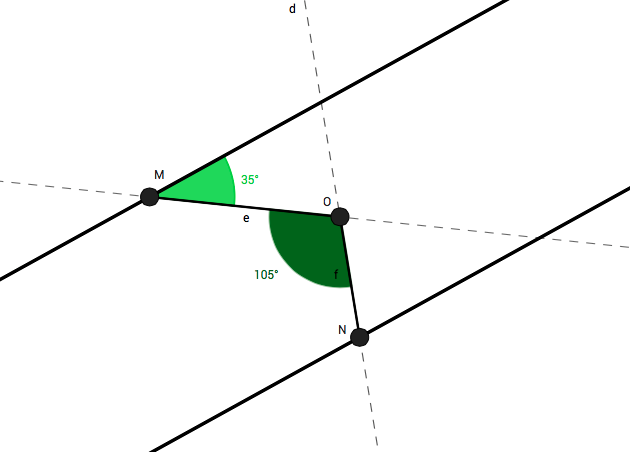
Next, we can observe the opposite angle of ∠ M O N , which according to the Vertical Angles properties, opposite angles are equal, thus δ = ∠ M O N
We also apply the supplementary angle property, as the two parallel lines are are cut by the same segment, thus splitting the straight angles (180º) in two supplementary angles, which have the same measurements in line l and m . Knowing that, we can trace the other half in line m [The two green angles].
We can also trace the straight angle forming in the segment that extends from
O
N
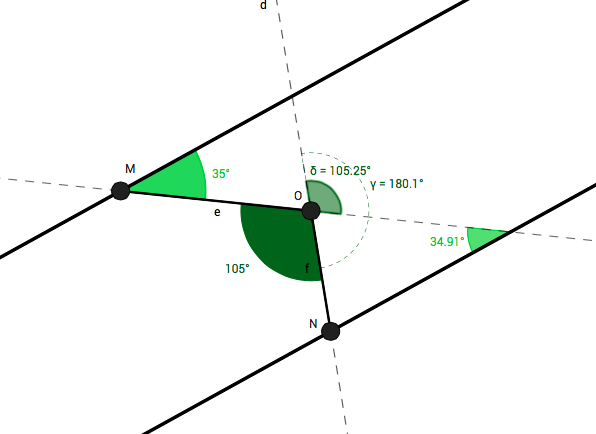
Using simple supplementary angle properties, we find the supplementary angle of δ (which would also be the supplementary angle of ∠ M O N if seen in the extended segment of M O ).
And lastly , observing the formed triangle △ N O P , we use the interior angle sum property (sum of internal angles of a triangle equals 180º) to solve easily for the desired angle.
3 5 ∘ + 7 5 ∘ = 1 1 0 ∘
1 8 0 ∘ − 1 1 0 ∘ = 7 0 ∘

This is just plain wrong!. The question asked for the angle on the LEFT side of point N, not the right side. So the answer is 110, not 70.
Log in to reply
It asks for the acute angle, which cannot be 110. The picture is misleading though.
@Larry McMahan The answer is right, the graphic I used to explain it was wrong, thanks for pointing it out.
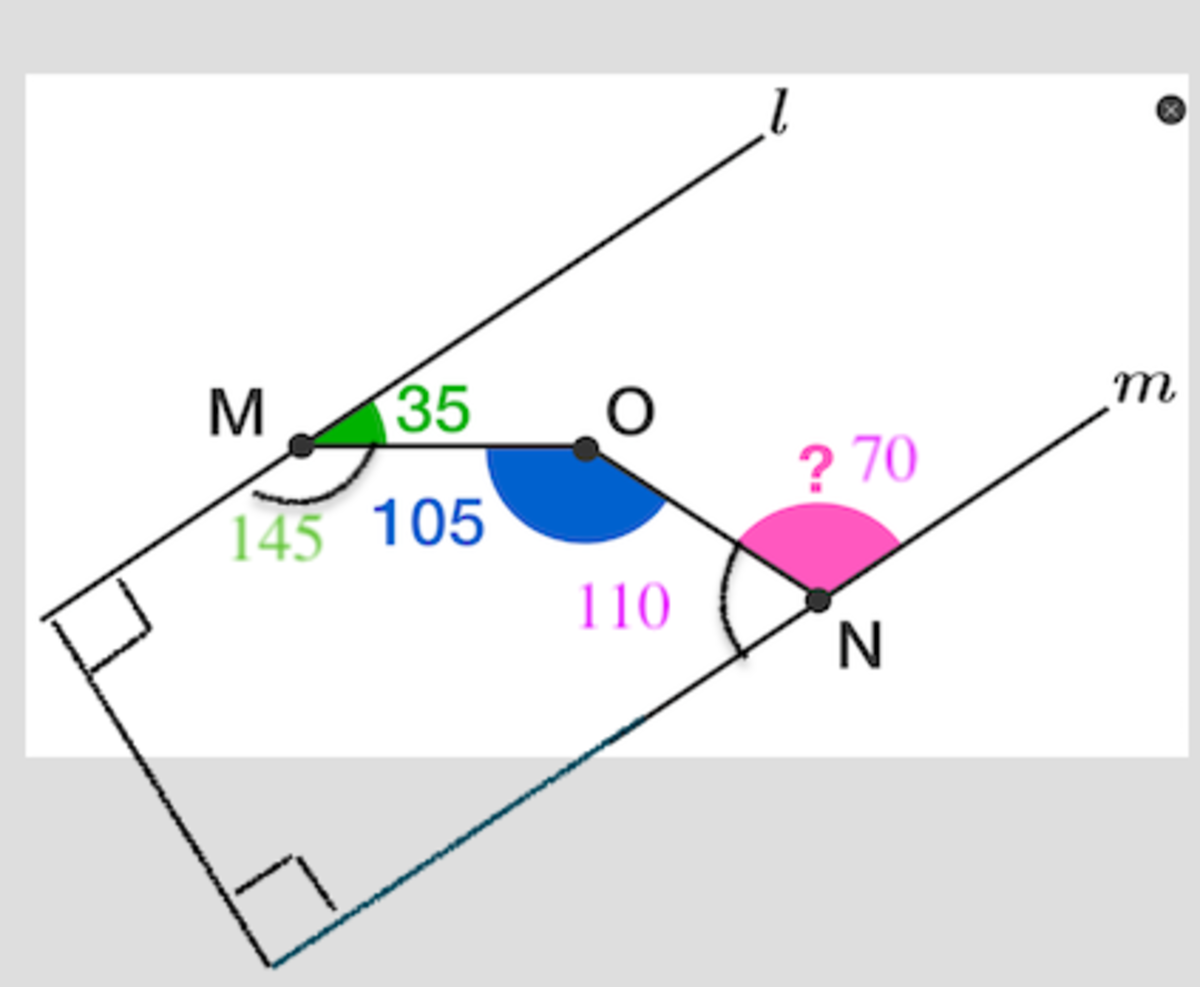
Sum of angles of a pentagon=540°
540-[(180-35)+105+90+90] = 110.
180-110= 70
70
Yaaaas I did it the same way except I made the Pentagon on the other side. Super easy
@Sharky Kesa does this seems right to you ?
As I have already mentioned, the diagram is not accurate. The question originally had the supplementary angle shaded, but people got confused and were giving the obtuse angle as the answer. It was fixed by Brilliant staff by switching the angles over, though it is now inaccurate. If you have a way to easily solve this dilemma, I pray you tell.
Log in to reply
see the comment above , does this seems right to you ? i guess its fine
Log in to reply
I had this diagram before and, like I said, people started submitting the obtuse angle rather than the acute.
Log in to reply
@Sharky Kesa – asking them for <ONm will solve the issue
Log in to reply
@Syed Hissaan – No, it won't. Supplementary angle could still be answered. I've written in the question a clarification. Is it better?
Log in to reply
@Sharky Kesa – well yes i agree that a supplementary angle could be answered if the person is attempting wrong. for some time leave the supplementary angle , if we just ask them to input the value that comes in <ONm they would always answer 70 if they are doing correct because supplementary angle comes in <ONp where p is any point(collinear) to mN (that lies on the left side ON) .
Log in to reply
@Syed Hissaan – You still haven't answered my question.
Log in to reply
@Sharky Kesa – yes that's better than the previous one , but can still confuse the solver
There is a super easy way
simple solution: draw a line parallel to lines l and m that passes through point O (call it line o). The acute angle between MO and o must be same as between MO and m, i.e. 35 degrees, so angle MON minus 35 degrees must be the same as the acute angle between m and NO - i.e. 105-35 = 70
This was the intended solution. :P
The other solutions had different constructions, but I found this on to be the simplest by far.
lateral thinking helps a lot - i never use a sledgehammer to crack a walnut :)
Also, the original diagram is misleading. I solved for 110 degrees almost immediately, because that is the angle shown; only to realize they were asking for the acute angle, which was of course its supplement.
Log in to reply
It was dodgy before, when it shaded the supplementary angle to the current one, because people saw that angle was obtuse. The overall diagram is just bad, sorry.
make a line n through O parallel to the other lines with end points P on the left and Q on the right. then angle MOP = 35 and angle PON = 70 and since line n is parallel to line m our angle in question is also 70.
Imagine a third parallel line called PQ cutting through the centre O. The angle MOQ would therefore equal to 145 as the angles are supplementary. 145 + 105 =250, 360- 250 = 110, therefore NOQ would equal to 110 as there is 360 degrees around a point. Again as the angles are supplementary, 180 -110 = 70, therefore the angle mNO equals to 70.
Extend N O to meet line l at P . Extend M O to meet line m at Q ∠ M Q N = 3 5 ∘ and ∠ N O Q = 1 8 0 ∘ − 1 0 5 ∘ = 7 5 ∘ .
Therefore acute angle between m and N O is 1 8 0 ∘ − ( 3 5 ∘ + 7 5 ∘ ) = 7 0 ∘ .