Where is the ant after 2018 steps?
An ant begins from ( 0 , 0 ) in the x y -coordinate plane. It then travels to each point with non-negative integer coordinates following the pattern shown below.
If the ant stops moving after 2 0 1 8 units, find its final position ( x , y ) and enter your answer as x + y .
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
Moderator note:
The key strategy was here was establishing a geometric structure (in this case, counterclockwise or clockwise movement) that made it easy to establish a pattern.
In fact, if you recognized the visual proof of 1 + 3 + 5 + … + ( 2 n − 1 ) = n 2 , you have a clear way forward.
Yes, recognizing this arithmetic progress was what let me solve the problem in my head
Sir I still didn't understand why are we skipping the first box
Log in to reply
The pattern of odd numbers adding to squares (1 + 3 + 5 + ... + (2n - 1) = n^2) begins with 1, but the ant's pattern of steps begins with 3. So the first box is skipped to match the pattern of the ant's steps.
It turns out that the clockwise/CCW part doesn't actually matter. If each 'shell' traversed CCW, that would just swap the X & Y coordinates on the CW shells. Since the answer is given in terms of X+Y, swapping them has no effect on the answer.
I was off by one because of bad mental arithmetic :(
After 1 step, you reach ( 1 , 0 )
After 9 step, you reach ( 3 , 0 )
After 2 5 step, you reach ( 5 , 0 )
and so on...
After ( 2 n + 1 ) 2 step, you reach ( 2 n + 1 , 0 )
We know that 4 5 2 = 2 0 2 5 , so after 2 0 2 5 step, we reach ( 4 5 , 0 ) ,
track back to 2 0 1 8 t h step, we are at ( 4 4 , 6 ) , so the answer is 4 4 + 6 = 5 0 .
After 2025 steps wouldn't the ant be at (0,45)?
Log in to reply
No, 45 is an odd number, just like (1,0), (3,0) and (5,0).
Relevant wiki: General Term Pattern Recognition
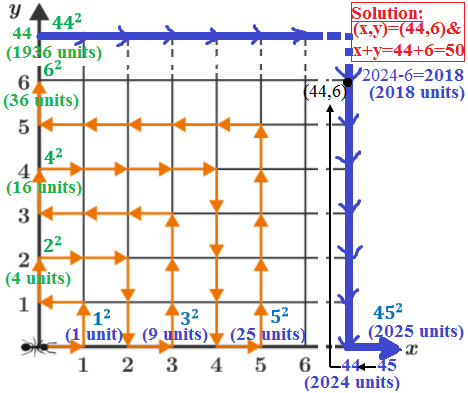 The ant will reach (45,0) at
4
5
2
=2025 units, (44,0) at
4
5
2
−
1
=2024 units and (44,6) at 2024-6=2018 units. The ant stops at (44,6) and the required solution is 44+6=50.
The ant will reach (45,0) at
4
5
2
=2025 units, (44,0) at
4
5
2
−
1
=2024 units and (44,6) at 2024-6=2018 units. The ant stops at (44,6) and the required solution is 44+6=50.
I n g e n e r a l : The ant will reach (n,0) at n 2 units & (n-1,0) at n 2 − 1 units where ′ n ′ i s o d d . Similarly, it will reach (0,n) at n 2 units & (0,n-1) at n 2 − 1 units where ′ n ′ i s e v e n .
Establishing pattern, we can see that in position (n,n) the number of steps = (1 + n) * n, so in position (44,44) number of steps = 1980, going 38 (2018 - 1980) steps down, the position will be (44,6), the sun is 50.
Thats how I did, too, took the position (n,n) and the number of steps n*(n+1)
In general, let n = a 2 + b with 0 ≤ b ≤ 2 a . Then the required sum is x + y = 2 a − ∣ b − a ∣ .
Since n = 2 0 1 8 = 4 4 2 + 8 2 , x + y = 2 ⋅ 4 4 − ∣ 8 2 − 4 4 ∣ = 8 8 − 3 8 = 5 0 .
I guess I should derive this nice little equation... Let m = max { x , y } and k = min { x , y } . It is obvious that the required number x + y = m + k .
We observe that all points with maximum coordinate m are visited directly after all points with smaller maximum coordinate have been visited. Together they form a square of side m . This shows that the number of steps n to reach the 2 m + 1 points with a certain value of m lies between m 2 ≤ n ≤ m 2 + 2 m . The minimum coordinate k reaches its maximum value when k = m , after m 2 + m steps. Moving forward or backward leads to a corresponding decrease in the value of k ; therefore k = m − ∣ n − ( m 2 + m ) ∣ . If we write n = m 2 + b , this simplifies to k = m − ∣ ( m 2 + b ) − ( m 2 + m ) ∣ = m − ∣ b − m ∣ , so that x + y = m + k = 2 m + ∣ b − m ∣ as advertised.
You are always giving neat and supersolutions.
Log in to reply
The real challenge (which I conveniently ignored) is proving that my formula actually works...
Log in to reply
Slightly better to state the formula for ( x , y ) , in which case we can easily induct to prove that it holds under the various possible moves.
Log in to reply
@Calvin Lin – By working with x + y instead of ( x , y ) separately, I avoid some of the work. See my extended solution.
I'm sure many strategies are possible but I started by finding a place to "hold on to". In this case, I decided I would study at which points the ant reaches the coordinates ( 0 , 2 k + 1 ) . At step 3 it is in ( 0 , 2 × 0 + 1 ) and after that it needs to move 1 up, then 2 × 0 + 2 times to the right, then 2 × 0 + 2 down, then move 1 to the right, then 2 × 0 + 3 up and finally 2 × 0 + 3 to the left and it reaches the coordinate ( 0 , 2 × 1 + 1 ) .
Generalizing, if the ant is at the coordinate ( 0 , 2 k + 1 ) , it needs to move 1 + 2 ( 2 k + 2 ) + 1 + 2 ( 2 k + 3 ) = 8 k + 1 2 steps to move to ( 0 , 2 ( k + 1 ) + 1 ) .
If we add up, we find that starting from ( 0 , 0 ) , to move up to ( 0 , 2 n + 1 ) we need to do 3 + ∑ k = 0 n − 1 8 k + 1 2 = 4 n 2 + 8 n + 3 steps.
Solving the inequality 4 n 2 + 8 n + 3 < 2 0 1 8 to get n ≤ 2 1 we find that at step 1 9 3 5 the ant is at ( 0 , 2 × 2 1 + 1 ) . Continuing the pattern, it then needs to move one up. (1936 steps). Then it moves 2 × 2 1 + 2 = 4 4 to the right (1980 steps). And after that it starts going down, but it only goes down 2 0 1 8 − 1 9 8 0 = 3 8 steps and ends up at ( 2 × 2 1 + 2 , 6 ) = ( 4 4 , 6 ) . So the solution is 4 4 + 6 = 5 0 .
By observing the pattern we may recognize that on the horizontal axis (let's call it X) the number of steps from the ant in the values with odd numbers, 1, 3, 5,... is their square: 1, 9, 25, ... while on the vertical axis (Y) the even numbers are squared (2, 4, 6,... get to be 4, 16, 36,...), so:
Steps "s" on the X-axis (y=0): if x odd: s = x^2,
Steps s on Y (when x=0): if y even: s = y^2.
Now, by trying, we find that 45^2=2025 is the closest square value to 2018. 2025= 2018+7. I.e. after 2025 steps, the ant would be at the position x= 45 (odd) and y=0, or (45, 0).
To find the position after 2018 ant's steps, we count 7 steps back from (45, 0) following the pattern. If we did it right it should come out (44, 6). The sum of this position coordinates is 44 + 6 = 50. Done! :-)
Calling t the discrete time, let
s ( t ) = x ( t ) + y ( t )
l ( t ) = m a x ( x ( t ) , y ( t ) ) (level)
t f ( l ) = m i n ( t ∣ s ( t ) = l )
t l ( l ) = m a x ( t ∣ s ( t ) = l )
then each level has 2 ∗ l + 1 points, so
t f ( l ) = ∑ 0 l − 1 2 k + 1 = l 2
t l ( l ) = l 2 + 2 l = ( l + 1 ) 2 − 1 , so
l ( t ) = ⌊ t ⌋ , and
s ( t ) = 2 ∗ l ( t ) − ∣ l ( t ) 2 + l ( t ) − t ∣
so l ( 2 0 1 8 ) = 4 4 , s ( 2 0 1 8 ) = 2 ∗ 4 4 − ∣ 4 4 2 + 4 4 − 2 0 1 8 ∣ = 5 0
Let s = 2 0 1 8 be the number of steps taken,
Let b be the band in which the ant exists
b = ⌈ s + 1 ⌉ − 1 = 4 4
Let d be the relative distance of the ant in the band
d = s − b 2 = 8 2
Let U be one of the coordinates and let V the other coordinate
U V = b − ⌊ b + 1 d ⌋ × ( d − b ) = d − ⌊ b + 1 d ⌋ × ( d − b )
The actual coordinates flip for each band so let's compute
O = d m o d 2 if band is odd
E = 1 − O if band is even
Now we can compute the actual coordinates
X = E U + O V
Y = O U + E V
I solved the question by observing the pattern making triangular series of the form f(n) = 2 n . ( n + 1 ) , where n is a natural number.
Let me explain.
When the ant reached 2 on the x-axis, it completed 8 steps. At 4, it completed 24 steps and then at 6, it completed 48 steps, so on and so forth.
So for every 2 a t h position on the x-axis, it completed 8 b steps as shown:
| 2(a) | 8(b) |
| 2(1) | 8(1) |
| 2(2) | 8(3) |
| 2(3) | 8(6) |
| 2(4) | 8(10) |
... so on and so forth.
Furthermore, we observe that the values of b are forming a triangular series: 1, 3, 6, 10... whose n t h term would have the corresponding value of a = n for every 2 a t h position on the x-axis. For example, the 3 r d term in the series is 6. So a = 3, b = 6.
Given 2018 is not a multiple of 8, we observe that the matter will revolve around numbers near 2018, that is, 2016 and 2024 that are multiples of 8.
8 x 252 = 2016 steps; 8 x 253 = 2024 steps; 252 and 253 are one of the values of b as shown in the table above.
Given the above logic, let us form the following expression:
2 n . ( n + 1 ) = 253 (We did not take 252 because the ant would have already passed that point to complete 2018 units)
Solving this, we get n = 22. The other value of n = - 23 is invalid.
Therefore, 253 is the 2 2 n d term in the triangular series. 22 corresponds to a , which implies the ant would be at 2 x 22 = 44 or 4 4 t h position on the x-axis.
To find the y-coordinate, we simply subtract 2018 from 2024 and get 6.
So (x,y) = (44,6)
x + y = 44 + 6 = 50
Another way of solving is using the sum formula for.summing integers. To reach an even number on the x-axis the an that's walked 2 × 2 n ( n + 1 ) × + n edges. This rewrites to n ( n + 2 ) . Now solve this for the answer 2018 and you will find n = 44,..... Retrace 6 steps back and you are ther (44,6).
Ant leaves x axis on even numbers and leaves y access on odd numbers The steps needed to reach even number x is x sq, the number needed to reach odd number y is y sq. Nearest square to 2025 (45x45) So step back seven integers from 45,0
Write a MATLAB script and read off the picture :)
x=0; y=0; X=[];
for i=1:25
if x==0 && mod(y,2)==0
while x<y
x=x+1; % increase x upto y=x
X=[X [x;y]];
end
while y>0
y=y-1; % then decrease y to 0
X=[X [x;y]];
end
end
x=x+1;
X=[X [x;y]];
if y==0 && mod(x,2)==1
while y<x
y=y+1; % increase y upto y=x
X=[X [x;y]];
end
while x>0
x=x-1; % then decrease x to 0
X=[X [x;y]];
end
end
y=y+1;
X=[X [x;y]];
end
plot(X(1,1:2018),X(2,1:2018))
- The movement sequence is (1,1)=2 units, (2,2)=6 units (clockwise), (3,3)=12 units (anticlockwise) i.e. at (m,m), the units covered are always m (m+1) and at (m,n) and m being an even, ant moves clockwise from (m,m) & (m>n) the units covered are {m (m+1)+(m-n)} ; therefore taking m=44, steps taken are= 44*45=1980 and that means 38 steps (clockwise) more to reach 2018 units or (m-n)=38 or n=6; therefore at (44,44) ant starts moving down or clockwise to stop at (44,6) to complete 2018 steps, Therefore answer is 44+6=50
The way I solved it didn't use the clockwise and counter clockwise. Each spot that the integers were equal (2,2 3,3) I noticed were that integer multiplied by the next. At 2,2 there were 2 3 steps. At 5,5 there were 5 6 steps. Even integers the steps were decreasing on the y value, and odd integers were decreasing on x value. 44*45=1980, only 38 away from our target number. So I knew x was 44, and y is only 6 from being down to 0. Might not have been the intended way of finding the solution but it worked.
Recognizing that the elapsed travel at each contact with either axis and the unit move will characterize the progression as: 1, 4, 9, 16, ... -- associated with each step along either axis: 1, 2, 3, 4, ...
2018 is 7 less that 45^2, so counting backwards 7 units along the path takes one to (44,6), which coordinates sum to 50.
My starting point was to find out the number of steps that the ant has moved when he has 'finished' the way that it is going and changes direction. So after 3 steps he has finished going anticlockwise. And note that 3 = 1 (the edge) + 2. After 8 moves the ant has finished going clockwise - note that 8 = 2 (the edge moves) + 2 x (1+2). After 15 moves the ant has finished going anticlockwise - note that 15 = 3 (the edge moves) + 2 x (1 + 2 + 3). So after n 'finishes' the ant will have taken N moves, where N = n + 2 (1 + 2 + .... + n). Many people know that the sum of n numbers is n x (n + 1)/2 So N = n + 2 x [n x (n + 1)]/2. So N = n x (n + 2) (which is (n + 1)^2 - 1). 2018 is between 44^2 (which equals 1936) and 45^2 (which equals 2025) So after 43 'finishes' the ant has taken 43 x (43 + 2) steps, which is 1935 steps. Because 43 is an odd number, the ant must be on the y axis. So it is on (0,43). After one more move it is on (0,44). So that was after 1936 moves. In the next 44 moves the ant moves along the line y = 44, and arrives at point (44,44). So this is after 1980 moves (1936 + 44). The ant then moves downwards for the remaining steps. There are (2018 - 1980) = 38 remaining steps. And on each of these steps the ant reduces the y value of the co-ordinate by 1. So after the 2018th move, the y co-ordinate of the ant is 44 - 38 which is 6. So after 2018 movements the ant is on the co-ordinate (44,6). So x + y is 44 + 6 which is 50. Regards, David
(Lazy but quick solution): My idea was to identify a number sequence such that: a n = x n + y n for all pairs of coordinates ( x , y ) . If we manually list the first few terms in this "sequence", we get:
0, 1, 2, 1, 2, 3, 4, 3, 2, 3, 4, 5, 6, 5, 4, 3, 4, 5, 6, 7, 8, 7, 6, 5, 4, 5, 6, 7, ...
An OEIS search reveals that this is A213088 , The Manhattan distance to the origin while traversing the first quadrant in a taxicab geometry . Then, we can use the Python program listed in the linked OEIS sequence to generate the 2018 th term, namely 50 .
Following the diagram we can identify patterns to describe 'milestones' the ant hits after n steps. Using the notation (n, x, y) the pattern (4, 0, 2) (9, 3, 0) (16, 0, 4) struck my interest. That is (n^2, n, 0) for odd n, and (n^2, 0, n) for even n. We want 2018 steps, so we observe sqrt(2018) to be about 44.9, meaning we should look to 45^2 steps. That's (2025, 45, 0). From here it's easily stepped back: (2024, 44, 0) (2023, 44, 1)... (2018, 44, 6). Assuming one goofed the axis the ant is on (odd and even distinction), it's irrelevant since the behavior of steps is symmetric and the answer desired is x+y. So whether you got (x, y) : (44, 6) correct or (6, 44) close, you still get 50.
Python code to brute force coordinates:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
|
You still can do much better code by knowing that the diagonal positions can be calculated easily. Any point on the diagonal ( n , n ) be reached after n × ( n − 1 ) steps.
Log in to reply
Yes, it could have been done if I had thought of programming the pattern itself. Like I noted, it was a brute force approach -- very inefficient.
Mathematica code:
f[{0, 0, 0}] := {1, 0, 2};
f[{x_, 0, 4}] := {x + 1, 0, 2};
f[{x_, 0, 2}] := {x, 1, 2};
f[{0, y_, 3}] := {0, y + 1, 1};
f[{0, y_, 1}] := {1, y, 1};
f[{a , a , 1}] := {a, a - 1, 4};
f[{a , a , 2}] := {a - 1, a, 3};
f[{x , y , 1}] := {x + 1, y, 1};
f[{x , y , 2}] := {x, y + 1, 2};
f[{x , y , 3}] := {x - 1, y, 3};
f[{x , y , 4}] := {x, y - 1, 4};
Nest[f, {0, 0, 0}, 2018]
Where the first two give us the position of the ant,while the third stands for the direction the ant going. Then iterate for 2018 times, Which gives us {44, 6, 4}, the position of ant is(44,6), Thus the answer is 50.
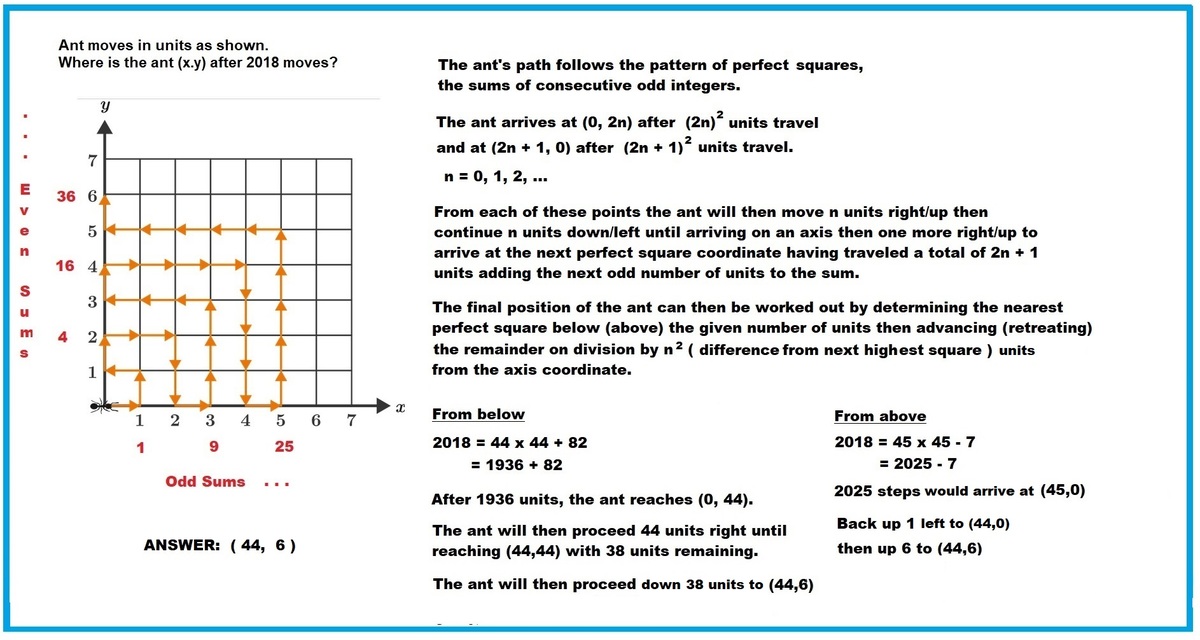
Let’s recolor the ant’s steps and use red for counterclockwise steps and blue for clockwise steps:
The ant starts out with 3 steps counterclockwise, then 5 steps clockwise, then 7 steps counterclockwise, then 9 steps clockwise, and so on, in increasing odd numbers. Squares of consecutive integers also increase in odd numbers, so let’s picture the ant’s steps with concentric squares instead of arrows, leaving the first square blank since 1 is skipped, but still using red for counterclockwise steps and blue for clockwise steps:
Now we can see that when the ant reaches the 2 on the x -axis it has gone 3 + 5 = 3 2 − 1 = 8 steps, when it reaches 4 on the x -axis it has gone 3 + 5 + 7 + 9 = 5 2 − 1 = 2 4 steps, when it reaches 6 on the x -axis it has gone 3 + 5 + 7 + 9 + 1 1 + 1 3 = 7 2 − 1 = 4 8 steps, and so on. In general, when the ant reaches 2 n on the x -axis, it has gone ( 2 n + 1 ) 2 − 1 steps.
The number 2 0 1 8 is 7 less than the square number 2 0 2 5 (the square of 4 5 ), and 6 less than 2 0 2 4 = ( 4 4 + 1 ) 2 − 1 . Therefore, after 2 0 1 8 steps the ant is 6 above the 4 4 on the x -axis, for a coordinate of ( 4 4 , 6 ) , and 4 4 + 6 = 5 0 .