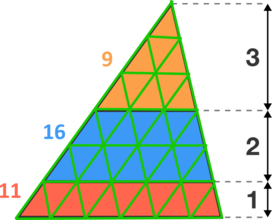
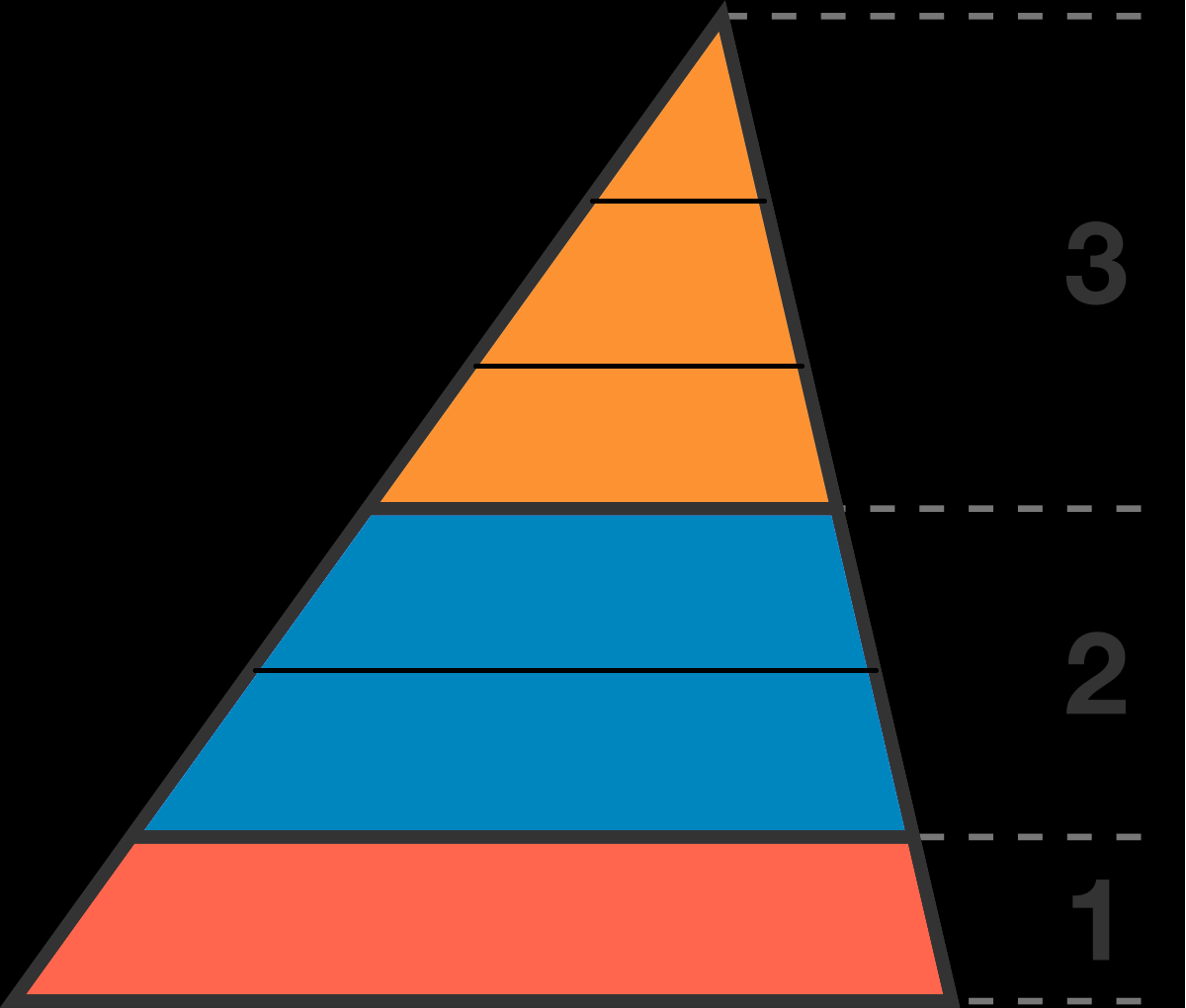
Which Area is the Largest?
The segments dividing this triangle are parallel to the triangle's base.
Which colored area is the largest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
this triangle is just a case from many, they're many triangles with the same height (6).
Playing around...
 I used Cavalieri's principle to make a right triangle
I used Cavalieri's principle to make a right triangle
Excellent and succinct solution. I based my answer on the blue segment being the closest in shape to a square, thus likely to have a larger area than either the wide but shallow red trapezoid or the tall but narrow orange triangle.
It doesn't say that 2 is twice 1 and that 3 is three times. They are not given as measurements, but just segments. Misleading puzzle.
Log in to reply
The fact that the numbers 1, 2 and 3 appear with double ended arrows next to them makes it absolutely clear that they are intended as measurements. Without those numbers being measurements the question becomes a matter of guesswork. With them one can work out the answer in various different ways. The solution on which you posted this comment happens to be a particularly good one.
+1 Irwin Price. Totally agree.
Jose - Smart & Simple Solution!
Beautiful answer
Amazing answer! Not always we need complicated equations to determine somethings!
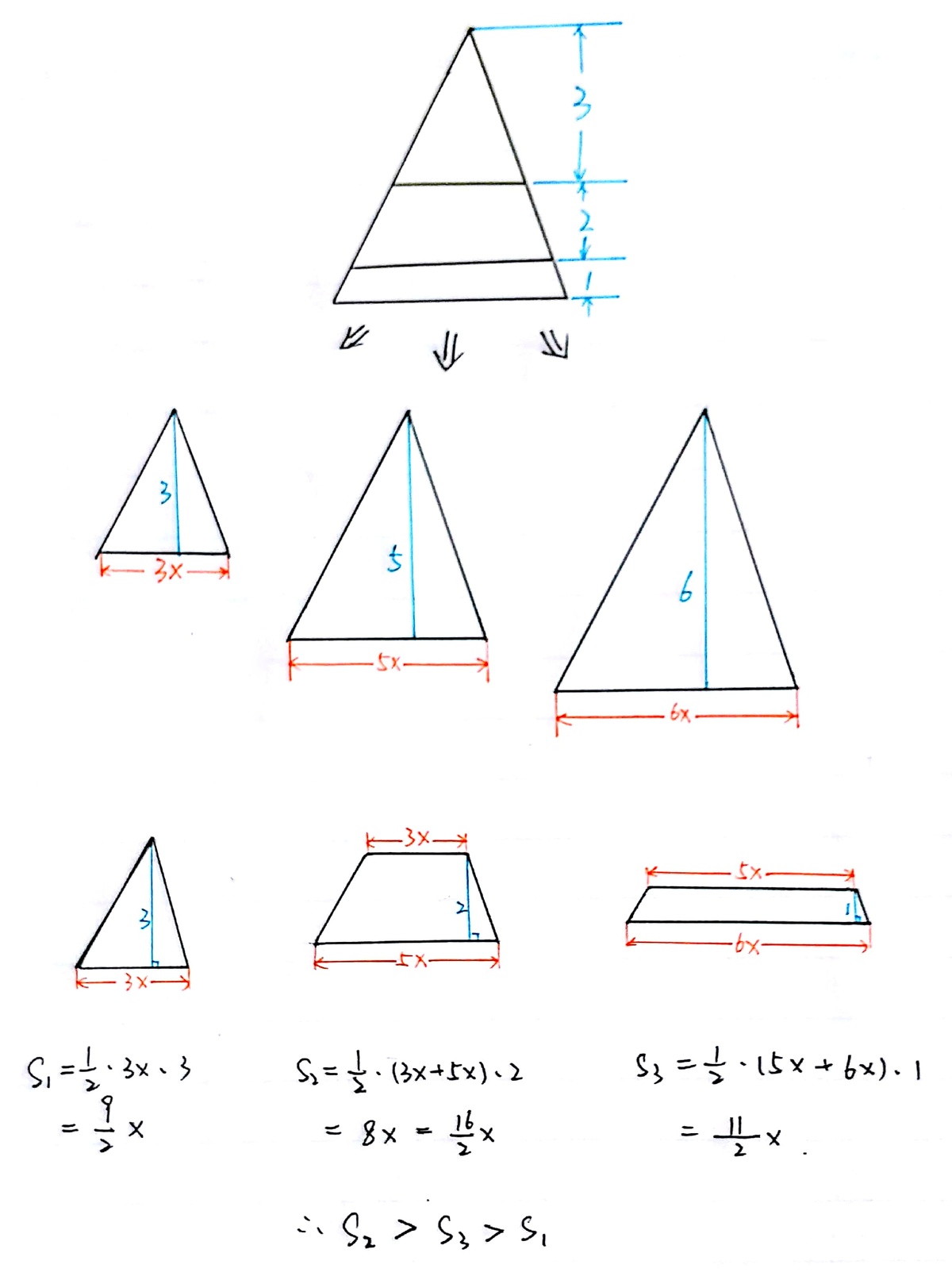
They are similar triangles so the ratio of
Orange : Orange + Blue : Orange + Blue + Red = 3^2 ; 5^2 : 6^2 = 9 : 25 : 36
So Blue = 25 - 9 = 16 and Red = 36 - 25 = 11
Therefore Area Orange : Blue : Red = 9 : 16 : 11 so blue is biggest
The diagram shows three similar triangles, of heights 3, 5, and 6 respectively. Their areas are proportional to the heights; thus we have A 1 : A 2 : A 3 = 3 2 : 5 2 : 6 2 = 9 : 2 5 : 3 6 . The blue area is the difference between the second and first triangle; the red area is the difference between the third and second triangle. Thus orange : blue : red = 9 : ( 2 5 − 9 ) : ( 3 6 − 2 5 ) = 9 : 1 6 : 1 1 . Thus the orange area is smallest, the red is slightly bigger, and the blue area is almost twice as large.
Generalization
Suppose the triangle were divided into n trapezoidal sections, with height ratios n : ( n − 1 ) : ( n − 2 ) : ⋯ : 2 : 1 . Then the total area of the first k sections would be proportional to A 1 + ⋯ + A k ∝ ( n + ( n − 1 ) + ( n − 2 ) + ⋯ + ( n − k + 1 ) ) 2 = ( 2 1 n ( n + 1 ) − 2 1 ( n − k ) ( n − k + 1 ) ) 2 = ( 2 1 ( 2 n − k + 1 ) k ) 2 . Subtracting, we get A k ∝ ( 2 1 ( 2 n − k + 1 ) k ) 2 − ( 2 1 ( 2 n − k + 2 ) ( k − 1 ) ) 2 = k 3 − 3 k 2 ( n + 1 ) + k ( 2 n 2 + 5 n + 3 ) − ( n + 1 ) 2 . To see which of the areas A k is maximal, consider the difference A k − A k − 1 ∝ 3 k 2 − 3 k ( 2 n + 3 ) + ( 2 n 2 + 8 n + 7 ) = 3 ( n + 2 3 − k ) 2 − ( n + 2 1 ) 2 + 2 1 . This expression is positive for 1 ≤ k < k 0 and negative for k 0 < k ≤ n , where k 0 = n + 2 3 − 3 ( n + 2 1 ) 2 − 2 1 . This means that A k grows as long as k < k 0 but shrinks after that. Thus the maximum value of A k is obtained for the smallest integer k less then k 0 , i.e. A k is maximal ⟹ \ k = ⎣ ⎢ ⎢ ⎢ n + 2 3 − 3 ( n + 2 1 ) 2 − 2 1 ⎦ ⎥ ⎥ ⎥ .
The expression for k 0 may be approximated as k 0 ≈ n + 2 3 − 3 n + 2 1 = ( 1 − 3 1 ) n + ( 2 3 − 2 3 1 ) ≈ 0 . 4 2 2 6 5 n + 1 . 2 1 1 3 2 . This means that the section with the largest area is that with index k = ⌊ 0 . 4 2 2 6 5 n + 1 . 2 1 1 3 2 ⌋ ,
For the situation n = 3 in this problem, we obtain k = 2 , which means that the second section (the blue section) is largest.
Fun generalization.
doesin't the base also come into play
Log in to reply
If the old area is A = 2 1 b h , then the new area is A new = λ 2 2 1 b h , which follows linear algebra. Here, b and h are the old lengths, whereas λ b and λ h are the new lengths.
It's very interesting how Arjen looked at heights and areas, but not the bases.
In general, if (any two corresponding) linear dimensions of two similar figures are in ratio a : b , then their areas have ratio a 2 : b 2 . Specific details about the shape are not needed.
The orange and red area are not equal. Please check the calculation 36-25 which is equal to 11.
Nice analysis.
Wow. Very good.
Why am I not getting your generalisation?
Log in to reply
Dunno. The idea is simply to add sections to the top, of relative height 4, 5, 6, and so on.
This makes for more complicated math, but it's also more fun (I think). Let me illustrate with the example n = 5 . First, I calculated the areas of the triangles:
k 1 2 3 4 5 A 1 + ⋯ + A k = ( 2 1 ( 2 n − k + 1 ) k ) 2 A 1 = ( 5 ⋅ 1 ) 2 = 2 5 A 1 + A 2 = ( 4 2 1 ⋅ 2 ) 2 = 8 1 A 1 + A 2 + A 3 = ( 4 ⋅ 3 ) 2 = 1 4 4 A 1 + A 2 + A 3 + A 4 = ( 3 2 1 ⋅ 4 ) 2 = 1 9 6 A 1 + A 2 + A 3 + A 4 + A 5 = ( 3 ⋅ 5 ) 2 = 2 2 5
By subtracting, I obtained the areas of the trapezoidal sections: k 1 2 3 4 5 A k = k 3 − 3 k 2 ( n + 1 ) + k ( 2 n 2 + 5 n + 3 ) − ( n + 1 ) 2 = k 3 − 1 8 k 2 + 7 8 k − 3 6 2 5 − 0 = 2 5 = 1 − 1 8 + 7 8 − 3 6 8 1 − 2 5 = 5 6 = 8 − 7 2 + 1 5 6 − 3 6 1 4 4 − 8 1 = 6 3 = 2 7 − 1 6 2 + 2 3 4 − 3 6 1 9 6 − 1 4 4 = 5 2 = 6 4 − 2 8 8 + 3 1 2 − 3 6 2 2 5 − 1 9 6 = 2 9 = 1 2 5 − 4 5 0 + 3 9 0 − 3 6 From this table we see that k = 3 has the greatest area. This can be established "mechanically" by calculating the differences k 2 3 4 5 A k − A k − 1 = 3 ( n + 2 3 − k ) 2 − ( n 2 + n − 4 1 ) = 4 1 ( 3 ( 1 3 − 2 k ) 2 − 1 1 9 ) 5 6 − 2 5 = 3 1 = 4 1 ( 3 ⋅ 8 1 − 1 1 9 ) 6 3 − 5 6 = 7 = 4 1 ( 3 ⋅ 4 9 − 1 1 9 ) 5 2 − 6 3 = − 1 1 = 4 1 ( 3 ⋅ 2 5 − 1 1 9 ) 2 9 − 5 2 = − 2 3 = 4 1 ( 3 ⋅ 9 − 1 1 9 ) Because the last positive value in this list occurs when k = 3 , we know that A 3 is the largest area. We find the last positive value by determining the zero of the expression for A k − A k − 1 , 4 1 ( 3 ( 1 3 − 2 k ) 2 − 1 1 9 ) = 0 ∴ k = 2 1 ( 1 3 − 3 1 1 9 ) = 3 . 3 5 , so that the switch from positive to negative happens between A 3 − A 2 and A 4 − A 3 . Rounding down gives k = 3 for the largest area. A very good linear approximation simply gives k ≈ 0 . 4 2 2 6 5 ⋅ 5 + 1 . 2 1 1 3 2 ≈ 3 . 3 2 which also rounds down to k = 3 .
Arjen -- That is beautiful; If I study it for a month I might figure it out. :-) In the first sentence under Generalization you have "Suppose the triangle were divided into n trapezoidal sections...". For this situation you stated that the value of n is 3 -- but the 'top' section (call it the nth section) is not a trapezoid -- it's a triangle. Does that matter ?
Log in to reply
I think of a triangle as a degenerate trapezoid, with top base of length zero :)
Log in to reply
Now I will have to look up 'degenerate trapezoid'. :-)
Log in to reply
@Jesse Otis – Picture a trapezoid. Now imagine that one of the bases grows smaller and smaller, until eventually it hits length zero. Then it is degenerate.
In the same way, a point is a degenerate circle, a line segment a degenerate rectangle or ellipse, and so on.
Log in to reply
@Arjen Vreugdenhil – Thanks; I have a better idea of that now. Can a trapezoid 'degenerate' all the way into a line segment (i.e. if one base can go to zero length can the other base do so along with it) ?
( •̀∀•́ ),it's perfect~(≧▽≦)/~
A hell of a long description. Since everything is proportional simply now that if the large triangle base is 6 then the next base is 5 and the little triangle base is 3. Calculate areas and the blue is the largest.
Log in to reply
Just read the part above the line. The rest is a generalization to bigger triangles. If the triangle were divided into 100 parts in the same manner, calculating areas and deciding which one is larger would take a lot of work. But now that I did the work here, I can simply conclude that of the 100 pieces, the ⌊ 0 . 4 2 2 6 5 × 1 0 0 + 1 . 2 1 1 3 2 ⌋ = 4 2 + 1 = 4 3 th piece is the biggest.
Log in to reply
Great!!.. You are really awesome! @Arjen Vreugdenhil
Wonderful solution, but I was a bit stuck trying to figure out what is wrong with this similar line of reasoning.
The ratio of the areas of trapezoid with both the blue and red regions, A B + A R , to the blue trapezoid, A B , is,
A B A B + A R = ( 2 3 ) 2 = 4 9 , A B A R = 4 9 − 1 = 4 5
Therefore, A R is greater than A B . There must be some mistake here, but I can’t think of what it is.
Log in to reply
The ratio is not correct, because the two trapezoids you are considering are not similar.
Their height ratios are 3:2, as you correctly observe; but their bases have ratios 1:1 for the top base and 6:5 for the bottom base.
Is it necessary to square the heights? Are you just trying to get bigger numbers?
Log in to reply
The reason for squaring them is that the ratio of areas of similar figures is the square of the ratio of their linear dimensions.
Consider the simple case of two squares: if their sides have ratio s 1 : s 2 = 4 : 3 then their areas have ratio A 1 : A 2 = s 1 2 : s 2 2 = 1 6 : 9 . The same is true for other similar shapes; in this case, triangles.
A more graphical way to understand this: The length of the baseline (c) is proportional to the height (h): c ∼ h , and the area (A) proportional to the baseline and height A ∼ c ⋅ h , then that means the area is proportional to the square of the height: A ∼ h ⋅ h .
They are proportional to the heights, but the bases have different sizes, no?
Log in to reply
Yes, but the triangles are all similar. So the bases are in the same proportions as their heights.
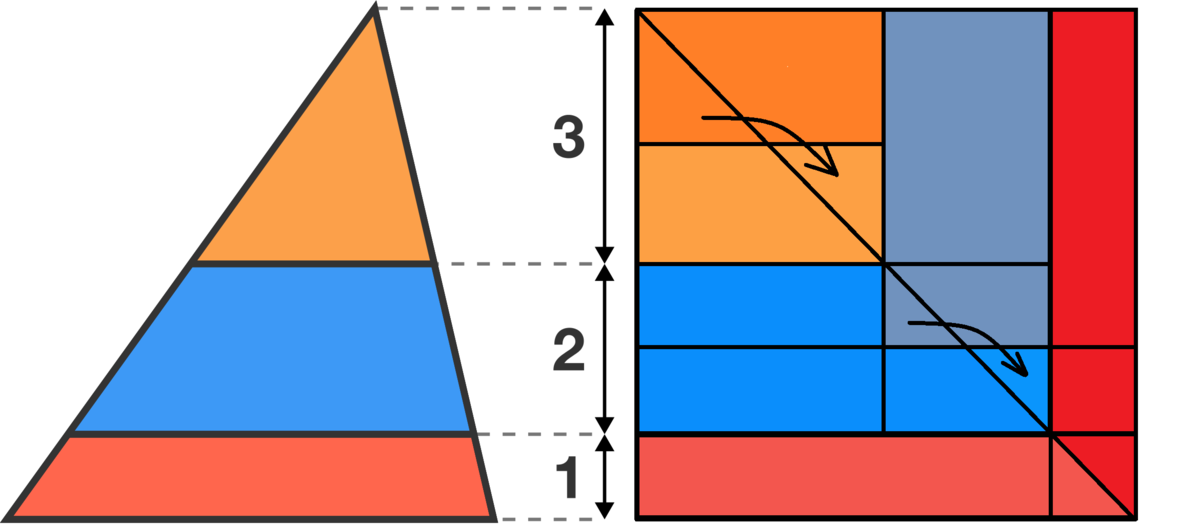
Use Cavalieri's principle to transform the given triangle to a right triangle, and then flip the triangle over to get a rectangle.
From the image below it's clear that the
blue area
is the greatest.
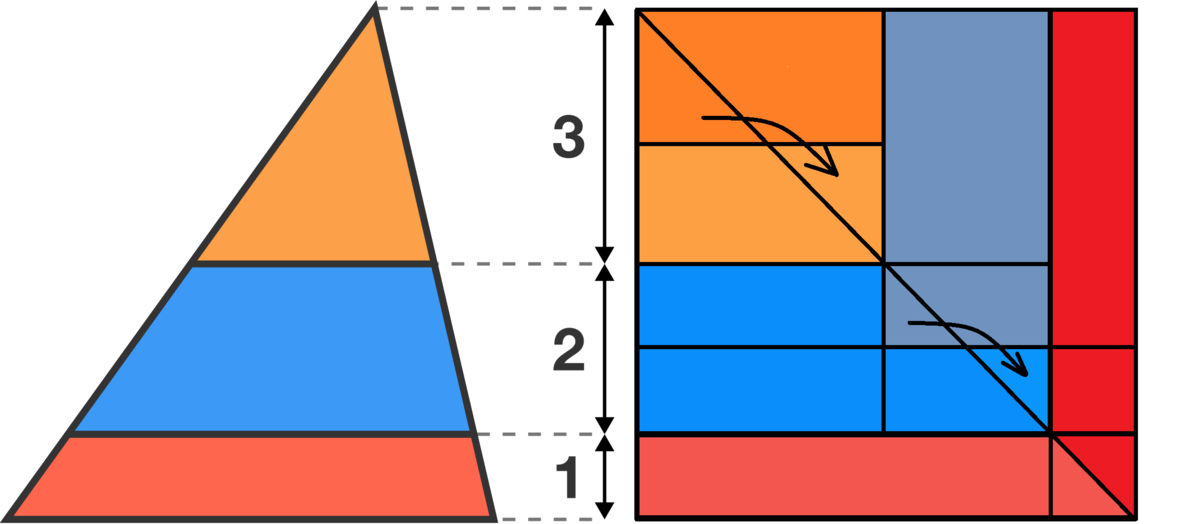
So, you are using shearing where you keep the base and height of the triangle constant so the areas of the original triangle and the right triangle are congruent.
Log in to reply
Exactly and not only that -- Cavalieri's principle guarantees me that segments retain their original area too.
Log in to reply
Which one can also quickly see if we look at the formula for the area of a tringle. Base x Height / 2. => every triangle with the same base and height have the same area.
Flipping it makes a rhomboid, which is not a square.
Simple. Beautiful. I did it like Arjen and just calculated it through, but this visual proof makes it so obvious.
Let b 1 be the base of the red area, b 2 the base of the blue area, and b 3 the base of the orange area.
By similar triangles, 3 + 2 b 2 = 3 + 2 + 1 b 1 , so b 2 = 6 5 b 1 . Also, 3 b 3 = 3 + 2 + 1 b 1 , so b 3 = 2 1 b 1 .
The orange area is the orange triangle with an area of A o = 2 1 b 3 ⋅ 3 , and since b 3 = 2 1 b 1 , A o = 2 1 ( 2 1 b 1 ) 3 = 4 3 b 1 .
The blue area is the blue trapezoid with an area of A b = 2 1 ( b 3 + b 2 ) 2 , and since b 2 = 6 5 b 1 and b 3 = 2 1 b 1 , A b = 2 1 ( 2 1 b 1 + 6 5 b 1 ) 2 = 3 4 b 1 .
The red area is the red trapezoid with an area of A r = 2 1 ( b 2 + b 1 ) 1 , and since b 2 = 6 5 b 1 , A r = 2 1 ( 6 5 b 1 + b 1 ) 1 = 1 2 1 1 b 1 .
Since 3 4 b 1 > 1 2 1 1 b 1 > 4 3 b 1 , the blue area has the largest area.
This one was the same that I made up. Is the most clear and precise solution. Graphical solutions are nice but more than a solution are a guide to formalize a solution.
this is the best solution in this discussion.
My answer too
Trapezoid area is height times average of top side and bottom side.
1x(6+5)/2=5.5 (red),
2x(5+3)/2=8 (winner),
3x(3+0)/2=4.5 (Top triangle)
If we graph the triangle in the Oxy-plane, where the most left corner of the triangle is at the origin
O
(
0
,
0
)
and label the top of the triangle as
T
(
t
,
1
+
2
+
3
)
=
(
t
,
6
)
and label the most right corner of the triangle as
A
(
a
,
0
)
, we will get the following:
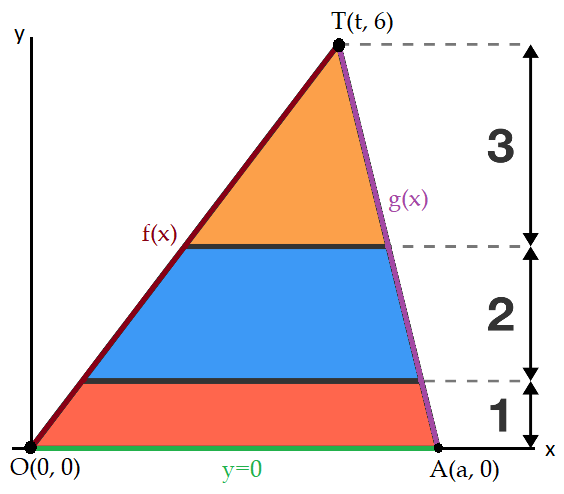 In this picture, I named the red line
f
(
x
)
, the purple line
g
(
x
)
and the green line is just the line
y
=
0
.
To get to a formula for
f
(
x
)
, we see the line goes through the origin and the point
T
(
t
,
6
)
, this implies that
f
(
x
)
=
Δ
x
Δ
y
⋅
x
=
t
−
0
6
−
0
⋅
x
=
t
6
x
. With the same strategy in mind, we can find that
g
(
x
)
=
a
−
t
−
6
(
x
−
t
)
+
6
In this picture, I named the red line
f
(
x
)
, the purple line
g
(
x
)
and the green line is just the line
y
=
0
.
To get to a formula for
f
(
x
)
, we see the line goes through the origin and the point
T
(
t
,
6
)
, this implies that
f
(
x
)
=
Δ
x
Δ
y
⋅
x
=
t
−
0
6
−
0
⋅
x
=
t
6
x
. With the same strategy in mind, we can find that
g
(
x
)
=
a
−
t
−
6
(
x
−
t
)
+
6
Now we want to find the coordinates of the intersections of f ( x ) and g ( x ) with the lines y = 1 and y = 1 + 2 = 3 , so we want to know the values of x that saturate the equations f ( x ) = 1 , g ( x ) = 1 , f ( x ) = 3 and g ( x ) = 3 . Isolating x in the 4 equations, will give us f ( 6 a ) = 1 , g ( 6 t + 6 5 a ) = 1 , f ( 2 t ) = 3 and g ( 2 t + 2 a ) = 3 .
With this information it is clear that the line y = 1 between the two intersections has a length of 6 5 a and that the line y = 3 has a length of 2 a . This implies firstly that the red area is equal to 2 a + 6 5 a ⋅ 1 = 1 2 1 1 a , secondly that the blue area is equal to 2 6 5 a + 2 a ⋅ 2 = 6 8 a and at last that the yellow area is equal to 2 2 a ⋅ 3 = 4 3 a . Because a is strictly positive, the blue area is the biggest. So, B l u e is the right answer.
Let the base of the big triangel be a. Then the area of the big triangel is T=a 6/2=3a. The area of the similar orange triangel is O=(1/2) (a/2) 3=(9/12) a; the orange and the blue together O+B=1/2 (5/6) a 5=(25/12) a hence B=(16/12) a. The red area R=T-(B+O)=3a-(25/12) a=(11/12)*a. B is largest.
draw a perpendicular through the triangle which will be of 6 units. then we will have two pairs of three similar triangles( both will have the height as a side).as they are similar, the ratio of heights and bases will be the same. calculate the areas of each color in the two triangles(we divided it into two with the height) then observe.BLUE HAS MAX AREA.
As you can see in the diagram above, the triangle is separated into 3 sections. Now, if you consider the base of each individual section as the value a then you can easily see, even at first glance, that placing each section through it's corresponding shape's area equation would place the parallelogram with height '1' to be the one with the one having the least area; hence having the colored area which is the smallest. So this eliminates the bottom section.
Now we are left with the two larger sections above. The one with height '2' being a parallelogram as well and the top most section with height '3' being a triangle. Now if you want to give values to the upper and lower horizontal lines for the parallelogram, do that at your own risk because every value is not suitable for every side of every shape. But if you need to do that at any cost, then please figure out the ratios of both these lines before giving ANY values to them.
Now looking at the figure, the triangle being at the top, has the smallest base which can also be imagined as 1/3 a , therefore it is smaller than the parallelogram which can have an imagined base of 1/2 a . But since the parallelogram is a quadrilateral it will always have an area that is greater than a triangle of equal size. So there is really no need to look at the base at all. For example a triangle of size 1x1 or 2x2 would have less area when compared to a quadrilateral of size 1x1x1 or 2x2x2, and since the triangle is already smaller than the parallelogram there is no possible way for it to have a greater colored area than the parallelogram. In either case the middle section has a greater area than the bottom or top section, which comes to the conclusion that it is the largest colored area within the large triangle.
Except the parallelogram with height '1' does NOT have the least area. And the triangle has height 3, which is NOT "already smaller" than the parallelogram of height '2'... -.-
Log in to reply
That might be true, but did you consider that I am a teenager.
Log in to reply
I'm sorry that i haven't, but this still should not be an excuse for using incorrect terms and invalid reasoning...
Specifically, can you please try to not use the term "parallelogram" for trapezoids/trapeziums? A parallelogram is a quadrilateral with two PAIRS of parallel sides. Meaning both pairs of opposing sides need to be parallel.
Let b represent the base length of the triangle. Now imagine two points starting at either side of the base and moving inward at different rates so that the height from both points straight up to the sides of the triangle is always the same. These points can move inward until they meet beneath the top vertex, where the maximum height is reached. Call the combined movement inward by both points x , and the height of the triangle's sides directly above both points after this movement y . These are related by a constant ratio since the sides of the triangle have constant slope. When the points meet beneath the top vertex, their combined movement is equal to the base length, b , and the height above them is 6, since this is the height of the vertex above the base according to the diagram. So, the constant ratio y x is 6 b . Thus, x = 6 b y . Using this fact, when y = 1 (top of the red region), x = 6 b , while when y = 3 (top of the blue region), x = 2 b . The new base length at a given height is equal to b − x , since x is the distance moved inward, so b 1 = 6 5 b and b 3 = 2 b , where b 1 and b 3 denote the base lengths at y = 1 and y = 3 , respectively. Using the triangle area formula A = 2 1 b h , the total area of the triangle ( A 0 ) as well as the areas from y = 1 up ( A 1 ) and from y = 3 up ( A 3 ) can be calculated:
A 0 = 2 1 ⋅ 6 b = 3 b A 1 = 2 1 ⋅ 6 5 ⋅ 5 b = 1 2 2 5 b A 3 = 2 1 ⋅ 2 1 ⋅ 3 b = 4 3 b
The area of the red region is the total area of the triangle ( A 0 ) minus the area above the red region A 1 . The area of the blue region is the area above the red region minus the area of the orange region, and the area of the orange region is simply A 3 . So, the calculations are:
A r e d = A 0 − A 1 = 3 b − 1 2 2 5 b = 1 2 3 6 b − 1 2 2 5 b = 1 2 1 1 b A b l u e = A 1 − A 3 = 1 2 2 5 b − 4 3 b = 1 2 2 5 b − 1 2 9 b = 1 2 1 6 b A o r a n g e = A 3 = 4 3 b
A b l u e is the largest of these.
First, we can divide the triangle into 6 sections in which in each step to the top, it is 1/6th of lesser than before. (as in each level 1/6 is deducted, we assume that the ratio between each level is consistent)
 Using the formula to find the area of a trapezoid A=h(a+b/2), we can try to estimate each section of the triangle.
Using the formula to find the area of a trapezoid A=h(a+b/2), we can try to estimate each section of the triangle.
- With the first slab being 1(6/6 + 5/6)/2 = 11/12
- On to the second slab: 2(5/6 + 3/6)/2 = 4/3 (2 and 2 cancel out, leaving 8/6 which is 4/3 )
- Third slab: (3/6 x 3)/2 = 3/4 (Since this is a triangle, not a trapezoid)
We can see that the second section (the blue one) is bigger.
My logic goes a little something like this:
-The horizontal lines only represent the level of each slab out of 6 total level. In other words the height only. (1/6 is 1 out of 6 levels)
-First, there's a total of 6 levels that's proportionally stacked on top. (in other words, the height is 6)
-It is a triangle that is slightly slanted to the right, otherwise, there is no discernible difference. (I'm sure there are some math and explanation to this in which I will not go into because I'm just a rookie)
-I assumed that at each level, the ratio is 1/6 lesser than the level beneath it.
Are each of these lines representing 1/6? so when du look at the whole figure, the last line is 6/6?
and how did u get (5/2 + 4/6)/2? Could you explain in more details?
Log in to reply
To answer your question:
-The horizontal lines only represent the level of each slab out of 6 total level. In other words the height only. (1/6 is 1 out of 6 levels)
-(5/2 + 4/6)/2; 2 is the height of the trapezium or trapezoid. I miswrote it, I apologize and thanks for pointing that out. It's actually ((5/6 + 3/6)/2)2 which is 4/3.
I don't know how to explain the exact logic behind the geometry but, as you can see in @Jose Fernandez Goycoolea's answer, at the top. The base of the triangle is turned into 6 divisible slabs at proportional lengths on each level of the triangle.
My logic goes a little something like this:
-First, there's a total of 6 levels that's proportionally stacked on top. (in other words, the height is 6)
-It is a triangle that is slightly slanted to the right, otherwise, there is no discernible difference. (there are some math and explanation to this in which I will not go into because I'm just a rookie)
-Which means I can assume that at each level, the ratio is 1/6 lesser than the level beneath it.
I also updated the answer to be more clear.
Knowing that the centre of gravity of a triangle occurs at a third from the base in the vertical direction, and that a third of the total height in this case is 2, using intuition it's pretty safe to assume that it occurs in the blue region which has a height of two and covers the centre of gravity (where the most mass - in this case area - is distributed).
Umm... what if the values were 19, 2, and 9 (instead of the 3, 2, and 1) ? The center of gravity would fall within the strip that actually only covers 8% of the area. ;-)
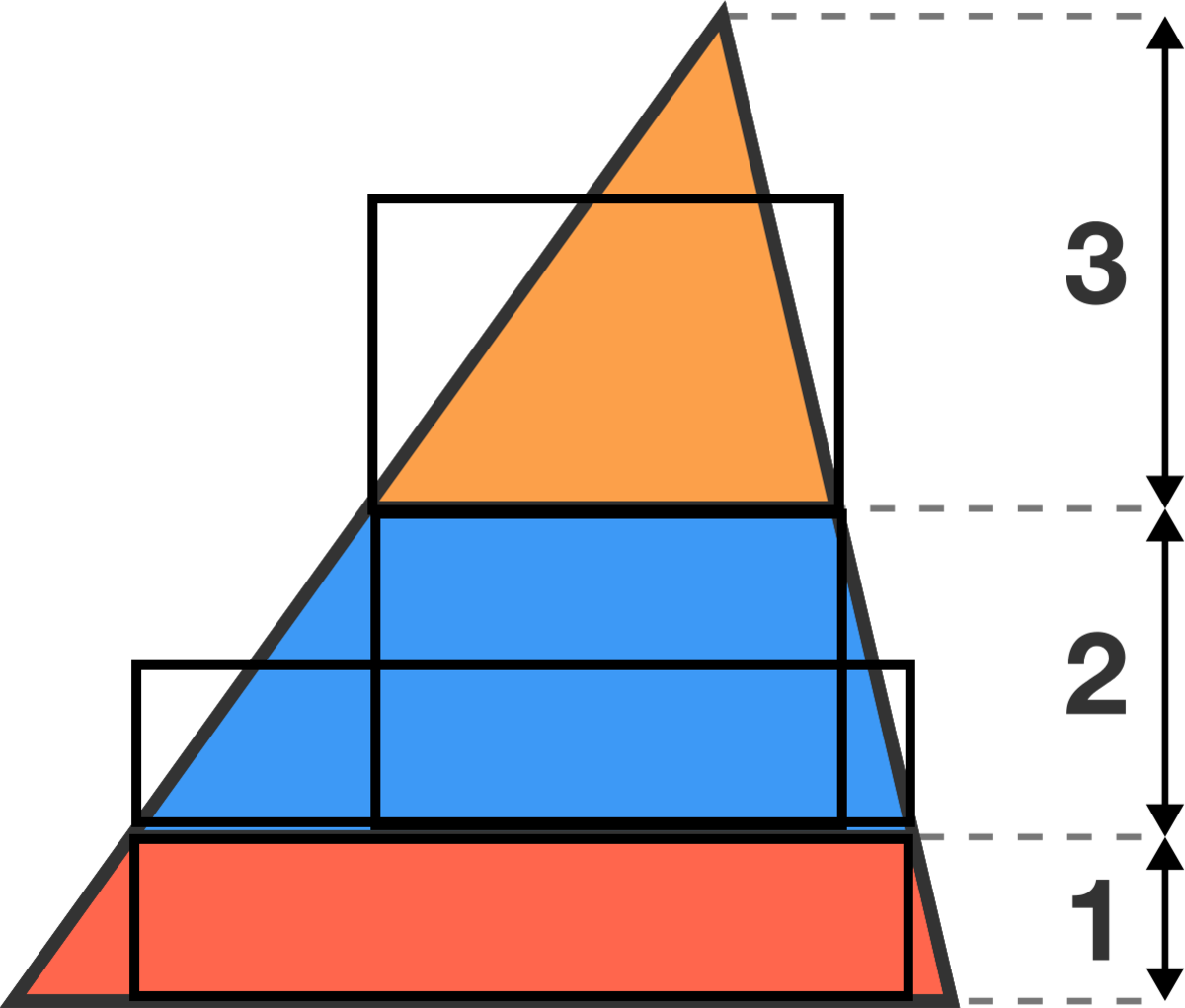
I superimposed a portion of the middle segment onto the top segment. You can see that the very top triangle that sticks out will not have enough area to cover the difference of the superimposed portion and the top segment.. For the next comparison the portion of the middle segment that is not covered by the superimposed rectangle is enough to cover not only the difference between the two but also the two tiny traingles that stick out from the bottom.
Total height of the triangle is 6. If the base is called B, we know (can be proven using trigonometry) that the base of the orange triangle is 2 B and the base of the triangle combined by the blue and the orange area is 6 5 B . Thus the red area is 1 2 1 1 B , the blue area is 1 2 1 6 B and the orange area is 1 2 9 B .
We can count the number of smaller triangular tiles, each one has the same area, so the section with more tiles is the largest