No real originality, but I can give anyone access to my new Brilliant currency (no bribe intent) lol

For every 4 flips of the fair coin. the biased coin is flipped 2 times.

The question implies that we have to compare the probability of the following scenarios ('events' for mathgeeks ):

1) All 4 flips of fair coin give head

2) All 2 flips of biased coin give tails

''Would it be easier to get 4 heads with the first coin, or get 2 tails with the second coin?'' is the same as asking ''Would it be easier to get 2 heads with the first coin, or get 1 tails with the second coin?'' Now lets compare these scenarios.

NOTE : Here though the probability would be different the inequality/equality would remain the same...

---

In 1st Scenario (Aim : 2 heads using fair coin)

Probability of getting heads in flip1 = $\frac{1}{2}$

Probability of getting heads in flip2 = $\frac{1}{2}$

Probability of 1st Scenario = $\dfrac{1}{2}$ * $\dfrac{1}{2}$ = $\dfrac{1}{4}$

---

In 2nd Scenario (Aim : 1 tail using biased coin)

It is given that the coin has a 75-25 bias in favor of Heads. so probability of getting tails is $\dfrac{25}{25+75}$ = $\dfrac{1}{4}$

---

Since both scenarios have a 1 in 4 chance Both are equally likely .

In the fair coin scenario, since the two outcomes of heads and tails are equally likely, the respective probabilities of a given sample point being the outcome is same for all the given sample points for the sample space "The coin is thrown 4 times" , which is

$S_{\text{f-4}}=(HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT)$

The probability of each of these sample points being the outcome must be $\dfrac{1}{2}×\dfrac{1}{2}×\dfrac{1}{2}×\dfrac{1}{2}=\dfrac{1}{16}$ , since there are sixteen $(2^4)$ , equally likely possibilities, consequently, we can say that the probability of outcome being $(HHHH)$ , is just that, $\dfrac{1}{16}$ .

A similar approach to the unfair coin gives us the sample space for the unfair coin, "The coin is thrown 2 times" given by,

$S_{\text{uf-2}}= (HH, HT, TH, TT)$

Here the probabilities for heads and tails are $\dfrac{75}{100}=\dfrac{3}{4}$ and $\dfrac{25}{100}=\dfrac{1}{4}$ respectively. Thus the probabilities achieved by each of the sample points in the sample space $S_{\text{uf-2}}$ ,

$HH= \dfrac{3}{4}×\dfrac{3}{4} =\dfrac{9}{16}$

$HT= \dfrac{3}{4}×\dfrac{1}{4} =\dfrac{3}{16}$

$TH= \dfrac{1}{4}×\dfrac{3}{4} =\dfrac{3}{16}$

$TT= \dfrac{1}{4}×\dfrac{1}{4} =\dfrac{1}{16}$

We see the sample point $(HHHH)$ in $S_{\text{f-4}}$ and the sample point $(TT)$ in $S_{\text{uf-2}}$ both are equally likely having a probability of $\dfrac{1}{16}$ .

Let H denote Heads, and T denotes Tails

For the 4 Heads case - the possibilities are

• (H,H,H,H)
• (H,H,H,T) and its permutations
• (H,H,T,T) and its permutations
• (H,T,T,T) and its permutations
• (T,T,T,T)

There are total of 16 possibilities out of which (H,H,H,H) is only 1 possibility. Therefore it's probability = $\frac{1}{16}$

For the 2 Tails case - the possibilities are

• (H,H) -> 9 times because H has $\frac{3}{4}$ chance, therefore H×H = $\frac{3×3}{4×4}$ = $\frac{9}{16}$
• (H,T) and its permutations-> 3 times because H has $\frac{3}{4}$ chance, therefore H×T = $\frac{3×1}{4×4}$ = $\frac{3}{16}$
• (T,T)

There are total of 16 possibilities out of which (T,T) is only 1 possibility. Therefore it's probability = $\frac{1}{16}$

Therefore both cases are equally likely.

$X: getting\space 4\space heads\space with\space the\space first\space coin\space in\space all\space 4\space throws$ $Y: get\space 2\space tails\space with\space the\space second\space coin\space in\space all\space 2\space throws$ $\red{Theorem:\space If\space in\space an\space experiment\space the\space probability\space of\space an\space event\space A\space is\space P(A)\space and}$ $\red{the\space experiment\space is\space done \space n\space times\space then\space the\space probability\space that\space all\space the\space time\space event\space A\space will\space occur\space is\space P(A)^n }$ $Using\space the\space above\space Theorem$ $P(X)=\dfrac{1}{2^4}=\dfrac{1}{16}$ $P(Y)=\dfrac{1}{4^2}=\dfrac{1}{16}$ $\Rightarrow P(X)=\dfrac{1}{16}=P(Y)$ $Hence\space the\space answer\space is : Both\space are\space equally\space likely\space to\space occur$

The first one, is a fifty-fifty chance, which is $\frac{50}{100}$ , which simplifies to $\frac{1}{2}$

Because we have four flips for the first one, we need to multiply the probabilities.

$\frac{1}{2}$ times $\frac{1}{2}$ times $\frac{1}{2}$ times $\frac{1}{2}$ equals $\frac{1}{16}$

And for the other one, as it is twenty five - seventy five ( $\frac{25}{100}$ ), we can simplify it to make $\frac{1}{4}$

Two times we flip it, so we multiply twice.

$\frac{1}{4}$ times $\frac{1}{4}$ equals $\frac{1}{16}$

The answer is... $Both$ $are$ $equally$ $likely$

Most Common Solution -

Probability of Case $1$ - $(\dfrac{1}{2})^4 = \dfrac{1}{16}$

Probability of Case $2$ - $(\dfrac{1}{4})^2 = \dfrac{1}{16}$

Thus, both scenarios are equally likely.

Since the probability $\alpha$ of an event happening $n$ times is $\alpha^n$ , the probability of each outcome is
$\frac{1}{2}^4$ and
$\frac{1}{4}^2$ .
Because $\frac{1}{2}^2=\frac{1}{4}$ , we have $\frac{1}{2}^4=\frac{1}{4}^2$ , and since $\frac{1}{4}^2=\frac{1}{4}^2$ , the two outcomes have the same probability.

---

$\text{If the probability of getting a result of an unconditional event 'E' is P(E), the probability of getting it N times would be P(E})^N.$

---

$\text{Chance of getting 4 heads with the first coin} = (\frac{50}{100})^4 = (\frac{1}{2})^4 = \boxed{\dfrac{1}{16}}$

$\text{Chance of getting 2 tails with the second coin} = (\frac{25}{100})^2 = (\frac{1}{4})^2 = \boxed{\dfrac{1}{16}}$

$\text{Hence, both probabilities are equally likely. }$

INCOMPLETE

From the question, we have:
The chance of getting heads tossing the fair coin once is $\frac{1}{2}$ while the chance of getting tails tossing the biased coin once is $\frac{1}{4}$ .
Then we can use theorem ‘if the probability of event $A$ is $P(A)$ , the probability of the event $A$ repeated $n$ times is $P(A)^n.$ But why?

Explanation:

See this Venn diagram for example.

---

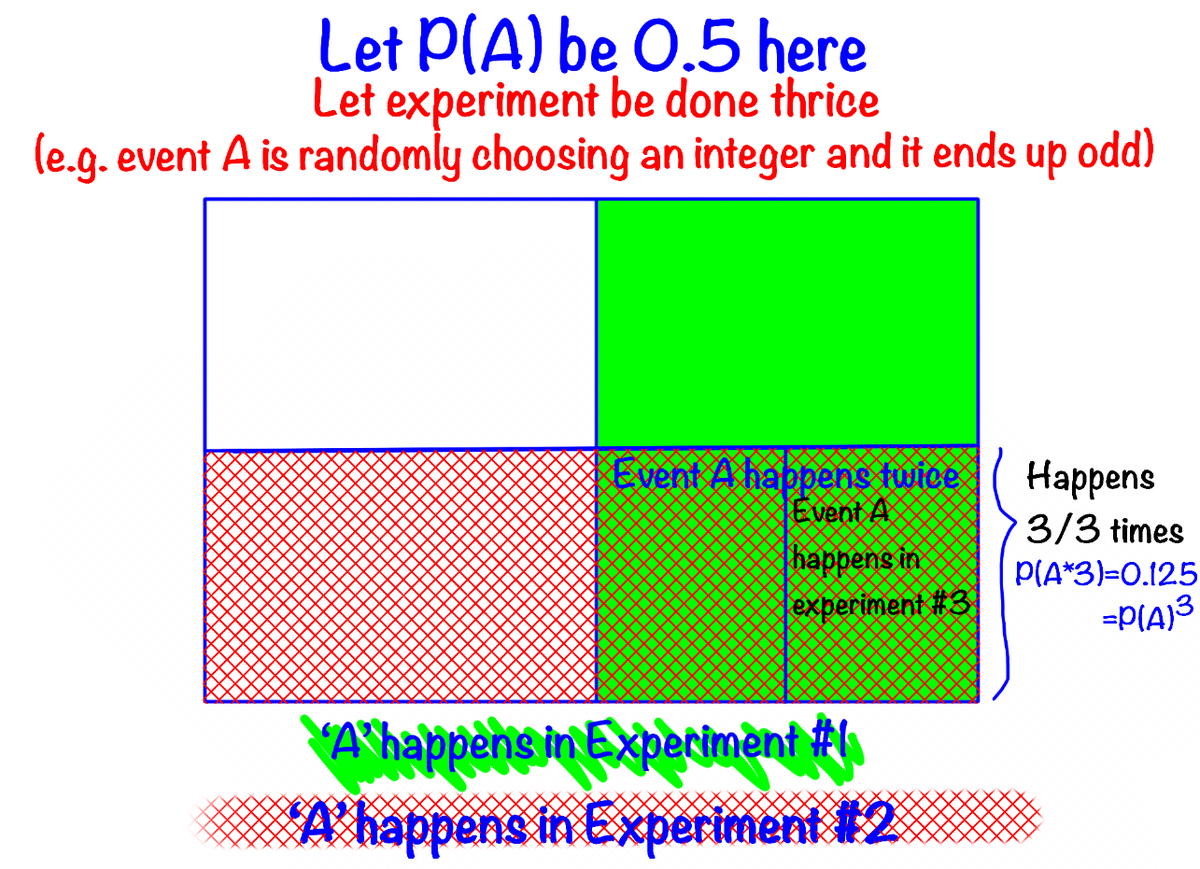
Therefore the theorem works.
The probability of getting four heads tossing the fair coin four times is $(\frac{1}{2})^4=\frac{1}{16}$ .
The probability of getting two heads tossing the fair coin twice is $(\frac{1}{4})^2=\frac{1}{16}$ .

So the two probabilities are equal.

Let the first coin be $\alpha$ , the second coin be $\beta$ , the probability for heads or tails with either coin $c$ be $p_c(H)$ and $p_c(T)$ and the probability for the final scenarios be $P_1$ and $P_2$ respectively. From the given values we can conclude that $\begin{aligned} p_\alpha(H) = p_\alpha(T) &= \frac{1}{2}\\[7pt] p_\beta(H) &= \frac{3}{4}\\ p_\beta(T) &= \frac{1}{4} \end{aligned}$ By using the multiplicative property of constant probabilities, we find $\begin{aligned} P_1 &= p_\alpha(HHHH) = p^4_\alpha(H) = \left(\frac{1}{2}\right)^4 = \frac{1}{16}\\ P_2 &= p_\beta(TT) = p^2_\alpha(T) = \left(\frac{1}{4}\right)^2 = \frac{1}{16}\\ \end{aligned}$ and therefore $P_1 = P_2.$

The two events $\textcolor{#D61F06}{{heads}}$ and $\textcolor{#CEBB00}{{tails}}$ are independent I.e.

probability of one's occurence or non-occurence will NOT affect the probability of the other one's.

Probability of independent events is given by:

$\textcolor{#67D94C}{P(E1∩E2)=P(E1)*P(E2)}$

Applying it to the first case , when the coin is ( $\textcolor{#69047E}{ unbiased}$ (unbiased coins have a probability of 50% each outcome))

Where, E1={HEADS}

E2={HEADS}

||ly,E3={HEADS}

E4={HEADS}

Visualization of the mentioned sets using Venn diagrams We have to find the probability of 4heads

E1∩E2∩E3∩E4={H,H,H,H}

$\textcolor{#20A900}{p(1H)=50\%=1/2(given)}$

$\textcolor{#D61F06}{p(E1∩E2∩E3∩E4)=(1/2)*(1/2)*(1/2)*(1/2)=1/16}$ [tossed 4 times]

Case 2 : when the coin is $\textcolor{#20A900}{ biased}$ (p(H)=75% and p(T)=25% =1/4 )(given)

Note that even if the coin is biased , probability of heads will not affect the probability of tails and vice versa

And, E6={TAILS} E7={TAILS}

E6∩E7={T,T} So,

$\textcolor{#D61F06}{P(T,T)=1/4*1/4=1/16}$ [tossed two times]

---

$\textcolor{#69047E}{P(4 heads)}$ in Case 1= $\textcolor{#69047E}{P(2 tails)}$ in Case 2

---

Probability {H,H,H,H}(unbiased)=probability {T,T}(baised)

Hence option (c) is correct,they are equally likely.

If we throw the first coin $4$ times, there are $16$ possible outcomes, which are: $HHHH, TTTT, HTTT, THTT, TTHT, TTTH, THHH, HTHH, HHTH, HHHT, HHTT, TTHH, HTHT, THTH, HTTH, THHT$ ( $H$ is heads and $T$ is tails). The probability of getting $HHHH$ is $1$ option that has all heads out of $16$ options that could possibly happen, which is $\frac{1}{16}$ . If we thrown the second dice twice, there are $4$ possible outcomes: $HT, TH, HH, TT$ . The probability of getting $TT$ is $\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}$ (Multiply it by $\frac{1}{4}$ because probability of getting $T$ is $\frac{1}{4}$ ). Since $\frac{1}{16} = \frac{1}{16}$ , Both are equally likely.

Probability of 4 heads in 4 tosses of fair coin : 4C4*(1/2)^4 = 1 * 1/16 = 1/16.

Probability of 2 tails in 2 tosses of biased coin with probability of tossing tails in a single throw = 0.25 or 1/4 : 2C2 * (1/4)^2 = 1/16.

Hence, both probabilities are equal

By the fundamental principle of counting, we know that since we need to throw the given number of dice, we need to multiply the probabilities of successive throws to get the probability of an event.

For the first event, the probability of getting a heads in one throw is $\dfrac{1}{2}$ (given). Since four throws are performed, the total probability is $\left(\dfrac{1}{2}\right)^4=\dfrac{1}{16}.$

For the second event, the probability of getting a tails in one throw is $\dfrac{1}{4}$ (given). Since two throws are performed, the total probability is $\left(\dfrac{1}{4}\right)^2=\dfrac{1}{16}.$

Hence, both events are equally likely.

Both are straight forward applications of binomial theorem:

First Scenario: ${4 \choose 4} \cdot \frac{1}{2} ^ 4 \cdot (1 - \frac{1}{2})^0 = {\frac{1}{2}} ^ 4 = \frac{1}{16}$

Second Scenario: ${2 \choose 2} \cdot \frac{1}{4} ^ 2 \cdot (1 - \frac{1}{4})^0 = {\frac{1}{4}} ^ 2 = \frac{1}{16}$

QED

For the first coin:

P(getting heads once) $=\dfrac{50}{100} = \dfrac{1}{2}$

P(tossing it 4 times and getting heads 4 times) $=\dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = \left ( \dfrac{1}{2} \right )^4 = \dfrac{1}{16}$

---

For the second coin:

P(getting tails once) $=\dfrac{25}{100} = \dfrac{1}{4}$

P(tossing it 2 times and getting tails 2 times) $=\dfrac{1}{4} \times \dfrac{1}{4} = \left (\dfrac{1}{4} \right )^2 = \dfrac{1}{16}$

---

$\because\dfrac{1}{16} = \dfrac{1}{16},$

P(tossing the first coin 4 times and getting heads) = P(tossing the second coin 2 times and getting tails)

Therefore $\boxed{\text{Both are equally likely}}$