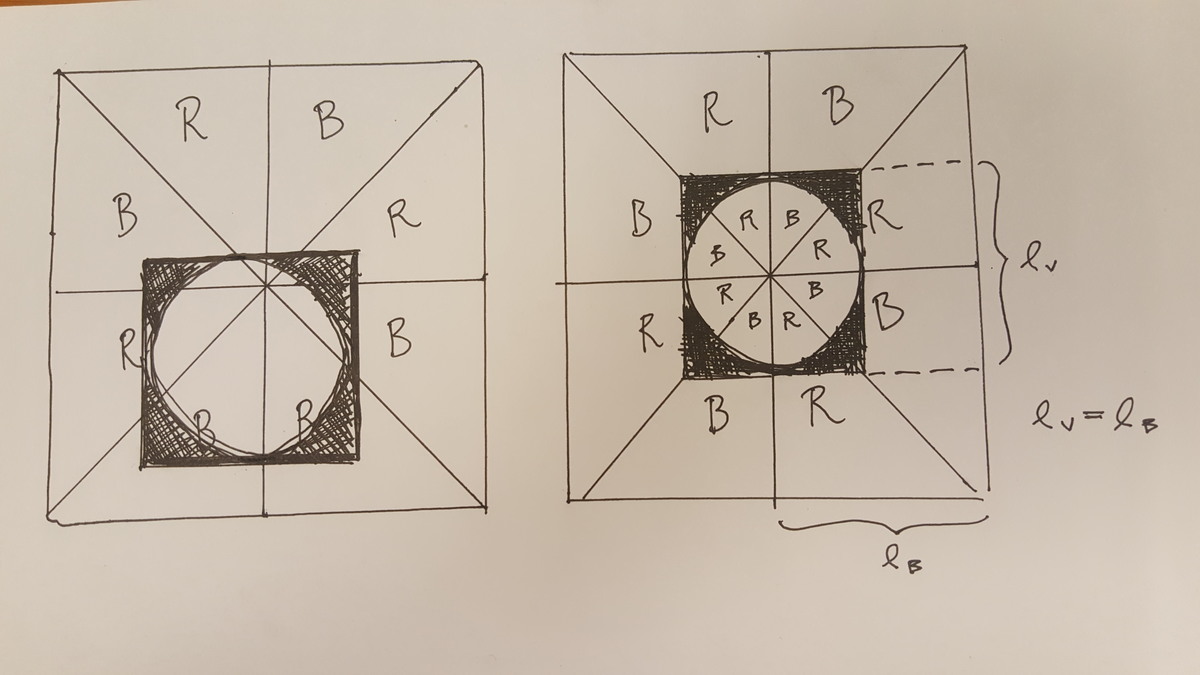
Which colored area is large?
The red and blue areas in the following 8 × 8 square are equal:
Are the red and blue areas still equal in the circle below?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Moderator note:
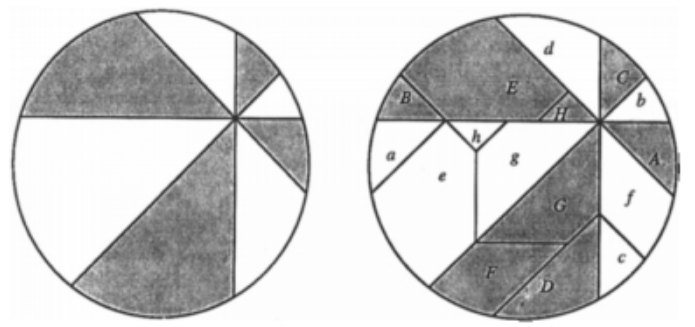
To state explicitly why the matching letters are congruent: note that they all represent either rotations or reflections of the circle. For example, M to M is a reflection over a horizontal axis, H to H is a 90 degree rotation, and A to A is a reflection over a diagonal axis.
I just counted the red squares in the first picture which had 32 red squares. I figured If I counted less or more red squares in the second picture then they would or would not be the same. And the second picture had less red squares. What is the flaw in my method? Your method honestly is still confusing me beyond comprehension
Log in to reply
the second picture also has less blue squares
you must count triangles.
Hi Sabastian
Check out the solution I've posted. I based it on David's solution, but I've spelled it out in a way that (I hope) is easier to follow.
I had some trouble understanding your comment, but I think perhaps you might have misunderstood the question? The question is about whether the red area (in the second picture) is equal to the blue area (in the second picture). It's not about comparing the first picture with the second picture.
I found comparing the pieces that were cut off easier to find.
you proved at a grid point, but this strategy can be generalize. So this proof is ok.
this visualization is so helpful!!!! But sir actually I had assumed that the rectangle had curled to form a circle so the pieces curl up symmetrically hence having no effect on the first case of the red and blue areas equal!! i would like to ask if this reasoning correct!!!!
Log in to reply
I think that since the center of the circle and the center of the slices are at different points, the pieces cannot be curled up symmetrically from the square to make the circle, but I am not sure.
My proof is based on probability. The intuition is that a dart can be thrown at two shapes with equal probability, then the shapes are of equal areas, and vice-versa. We are told that the blue/red shapes in the square are equal shapes, so a dart thrown at the square (we'll always hit the square, so P(S) = 1) will hit red or blue with equal probability. So P(S, R) = P(S)P(R) = 1/2, and P(S, B) = P(S)P(B) = 1/2.
When a dart hits an area of the circle, it hits a corresponding area of the square. The probability of hitting the circle P(C) happens to be pi/4, and while we don't really need to know this value, we'll use it for concreteness. So P(C, R) = P(C) * P(R) = P(C) * P(S, R) = pi/8 and P(C, B) = P(C) * P(B) = P(C) * P(S,B) = pi/8. Since P(C, R) = P(C, B), the red and blue shapes of the circle are of equal areas.
Log in to reply
But shouldn't one prove that the red area is equal to the blue area within a circle before stating that probability of hitting either is the same as for square?
Phrasing the question is key here. Is the question equating blue and red areas in each diagram or blue and red areas within each diagram?
Log in to reply
There is less red and blue in the circle compared to the square, so that is not what is being asked. The question asks if amount of red is equal to amount of blue in the circle.
But why are they congruent? I mean, they look about the same now you point it out! But I'm not readily able to see why this must be so.
Log in to reply
Each matching curved part is the same distance away from the center of the circle, which makes them congruent.
The usual phrase in maths or physics is "By symmetry". In this case, it's mirror symmetry &/or rotational symmetry.
For example, you can map the blue "C" square onto the red "C" square using mirror symmetry. If you placed a mirror-line at 45 degrees (from bottom left to top right), then the image of the blue C-square would map onto the image of the red C-square. The circle is symmetrical across this line, and the square grid is also symmetrical across this line, so you can be sure that the two shapes line up exactly.
Does that help?
What a clever question ;-;
It lacks of a little strictness,I think.
A dinamic solution https://ggbm.at/zPNyMMyx
Moderator note:
The Wikipedia page linked here mentions of a proof without words from 1994 by Larry Carter and Stan Wagon. Here is the original:
it says the site doesnt exist.
Log in to reply
it does, be careful not copy-pasting the : at the beginning of the url
Log in to reply
This link works better.
Log in to reply
@Filip Rázek – Looks like the original link has been updated now. :)
Very cool!
Looking at the question, I guessed that there would probably be a general proof for something like this. Otherwise it would have been quite an odd question for someone to come up with.
Is it true that if you can divide the (this) unfairly cut pizza into congruent pieces you can get a fair (equal) share of dark & light? If it is intuitive (subjective answer), can this be intuitively generalized? Is it also (or anyway) true that you get an equal share of edge crust?
The polar equation of the circle of radius 1 , measured from a point a distance x from the centre is (use the Cosine Rule) r = 1 − x 2 sin 2 θ − x cos θ
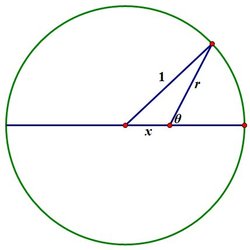
and so the area of a slice of the circle for α ≤ θ ≤ β is A ( α , β ) = 2 1 ∫ α β r 2 d θ = 2 1 ∫ α β [ 1 + x 2 cos 2 θ − 2 x cos θ 1 − x 2 sin 2 θ ] d θ = 2 1 ( β − α ) + 4 1 x 2 ( sin 2 β − sin 2 α ) − ∫ x sin α x sin β 1 − u 2 d u Rather than evaluating this explicitly, we use periodicity properties of the sin function to see that B ( α , β ) = A ( α , β ) + A ( α + π , β + π ) = ( β − α ) + 2 1 x 2 ( sin 2 β − sin 2 α ) and hence C ( α , β ) = B ( α , β ) + B ( α + 2 1 π , β + 2 1 π ) = 2 ( β − α ) Thus the area of the blue region is C ( α , α + 4 1 π ) = 2 1 π which is half the area of the circle for any value of α . The red and blue areas are equal.
Moderator note:
As mentioned in this comments, this proof is adaptable to more pieces. The theorem that the areas are equal (and assuming it must apply to any center possible) is true if the number of pieces is in the sequence 8, 12, 16, ... but false for all other even numbers. (Can you work out why?)
I usually don't like overkill solutions, but here I really like the second step (sin function periodicity), so yeah maybe I'm wrong and stereotypical. :)
Was going to type this out based on the over-simplified graphical answer. I don't think this is overkill I think it's robust mathematics. There's no proof "A equals A" necessarily just because they look the same, and there's no explanation of what made the squares chosen to "match" except visually. Arbitrary letter jumps to fit graphic goals.Weak sauce.
Log in to reply
The proof is in the symmetry (mirror, or rotation), but you are right it wasn't mentioned by David. I take the 'overkill' back, as this is a general solution (the point can be any point inside the circle).
Log in to reply
I would add that this argument can be adapted to prove the general result for cutting the pizza by 2 n equiangular slices
Log in to reply
@Mark Hennings – 4n, right? With 2n cuts. edit: n>1
Log in to reply
@Laszlo Kocsis – It all depends on whether the slice is the cut made with the pizza slicer, or the chunk of pizza that results. Thus 2 n slices with the slicer gives 4 n slices of pizza...
But sir actually I had assumed that the rectangle had curled to form a circle so the pieces curl up symmetrically hence having no effect on the first case of the red and blue areas equal!! i would like to ask if this reasoning correct!!!
I swear to god, one day, i will be able to understand that.
Log in to reply
Keep on learning. Have you studied polar coordinates?
Hi moderator, and thanx for modifying question. That is because the skale of these opposite areas is propotion to the angle. So 30° lines divide the areas to 1:5 (30°:150°).
This is not a solution but a comment - so I don't know if it will be posted. I want to say that I am SO jealous of all of you that post solutions to the problems; you ROCK. I am 66 years old and have struggled with mathematics all of my life; I so envy people like you that are good at it. I love to read your solutions to these problems - and I get to them, by my own admission, by taking wild guesses at the answers - most of which are wrong guesses (but with yes/no choices I have a 50/50 chance of being right). Kudos to all you math whizzes ! :-) d e n o m i n a t o r n u m e r a t o r (I had to add that LaTex fraction so that it would qualify as a solution and go through).
I don't think solutions are required include numbers or formulas.
Building on David Vreken's solution, I've spent a little time in MSPaint to see if I can break it down in a way that's easier to follow.

I've taken all the blue and red pieces, separated them out, and grouped them into a couple of separate images. First I've pulled out the full squares, and the 45 degree triangles. You can verify that the number of blue and red squares are equal, and the number of blue and red triangles are equal, just by counting.

Next, I've separated out the irregularly shaped pieces into three groups.You should be able to tell the area of each blue piece is identical to the area of a similar red piece. You can use either mirror symmetry or rotational symmetry (depending on the piece) to confirm that the areas really are identical.
Nice visual solution!
Log in to reply
Thanks! I don't think I could have done it without your answer to work from.
Things like this can be pretty time-consuming, but i find them very satisfying.
Great job on trying to illustrate this.
Very good solution.But this is time consuming.Is there any shorter process????????
A nice visual solution is to first assume we're actually looking at a larger object (illustrated below) through a smaller viewer. Now, if we center this viewer on the center of our object then the answer becomes clear. Any movement of our viewer from this center point always conserves red and blue since (for example) if we move towards red, we lose red on the other side. Any circularly symmetric object will cut out the same of each color within the viewer.
Liev, this is by far the best intuitive solution to this problem. Thank you and congratulations
I also think this is the best solution!
"First, convince yourself that if we move our viewer around then we always have equal amounts of blue and red"
To be honest, this is the difficult part. How do you prove that we will always have equal amounts of red and blue as we move the viewer around?
It doesn't seem intuitive or obvious to me.
Log in to reply
True, it's not obvious. I convinced myself of this by asking what would happen if I moved the view one square to the left, then I counted, and then I decided that this is true. Not a rigorous proof, that's for sure. But, hopefully, one that is interesting in a way that's different from the other solutions.
Log in to reply
Sorry, I misspoke (and wrote incorrectly in my solution). It becomes clear that there equal amounts of red and blue when you move the viewer to the center of the geometrical shape since it's symmetric.
Sorry, I misspoke (and wrote incorrectly in my solution). It becomes clear that there equal amounts of red and blue when you move the viewer to the center of the geometrical shape since it's symmetric.
I reasoned that the white corners were of equal area on all four corners therefore, the area of the colored areas must still be the same. It took me only a few seconds to come to the conclusion. I guessed and got it right. It was an intuitive response.
I did the same thing. I didn't prove it with a theorem, but rather the amount taken away when it's a circle, would still be proportional.
For this to be true, the amount of red and blue in the corners must be equal. In this case it is true, but still, it is immediately clear to me why.
It is not clear why both the blue and red areas removed from the four corners are equal, to prove they are you should adopt a similar reasoning as the basic solution so this wouldn't be an intuitive response.
Even though I was able to demonstrate so for this instance, I still could not see (or even intuit) that the corners outside the circle necessarily affected both colors the same, or that for every incomplete(non-square) red piece there has to be a congruent blue piece.
I might be able to do so if I could follow the reasoning (not given) of the formulaic algorithm given by Mark Hennings.
in the first picture,the red and the blue is equal.at the same time,the background picture is square, so when the two colour is filled in, the space should be divided half-and-half. now in the second picture, when the circle would be delimit in the square, the remain part would also be equal.
I did it the same way too!
Hi! I'm not here to add a solution, I was just wondering if anyone here who knows about the divergence theorem could explain how this is true in terms of that? For example in Physics we often use Gauss' Law which says: ∮ S E ⋅ d s = Q e n c / ϵ 0
And is often illustrated like this:

And in fact it didn't need to be the case that the charge be at the very center, it could have been anywhere in the circle. I'm just wondering if the solution to this problem and the law stated above are related somehow? And if not, does anyone know why they aren't related?
Pizza theorem: https://en.wikipedia.org/wiki/Pizza_theorem
they are still equal. This is because in the top pic. blue and red have equal areas. so it will be the same as splitting them in half; red and blue. then making it a circle will mean subtracting the same from both sides. then they would be equal.
First example, Fold the square by the vertical line (5:3) then we get perfect match for overlapping areas, then for the remaining not covered area move upper blue aria (two small square) to the bottom as a result we get 8 red = 8 blue in total (with triangles). Response = Yes Second example. Logical solution >> since the answer to the first question is Yes then by induction it is yes for the second part because there is no options apart from YES or NO.
The way I like to think of it is that it "treats" every area "fairly", which means the larger area a piece has, the more area it loses due to shaping the graph into circle, regardless of the color, and vice versa.
Each line that divides the circle are at 45 degrees, thus the circle will be divided in 8 parts where blues and orange are interleaved the area for each color will be the same
similar to my approach. I reasoned that if you divide the circle into the segments show but centered, then the answer is obvious. Now varying each line individually still maintains equivalence, so varying subsequent lines should still maintains the equivalence.
The red and blue areas are equal in the circle because each grid section with a red shape has a matching congruent grid section with a blue shape. The picture below shows how each square with a red curved shape matches each square with a congruent blue curved shape (A with A, B with B, and so on).
In addition, there are 13 red squares that correspond with 13 blue squares, and 6 red triangles that correspond with 6 blue triangles, which account for all the red and blue in the diagram.