Which comes first: tension or friction?

Classical Mechanics Level 3

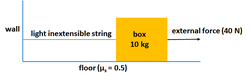Consider the idealized situation shown in the above figure. If $T$ refers to the tension in the string and $f$ refers to the frictional force between the box and the floor, select the correct option:

T = 10 \text{ N} \quad f = 10 \text{ N}

T = 20 \text{ N} \quad f = 20 \text{ N}

T = 40 \text{ N} \quad f = 0 \text{ N}

T=0 \text{ N} \quad f = 40 \text{ N}

None of the above

1 solution

Raj Rajput
Aug 14, 2015

I envy your handwriting.... :P

Yashwanth Manivannan - 5 years, 10 months ago

from that, i got to know that your handwriting is not good but handwriting doesn't matter as most of the competitive exams are objective :P

RAJ RAJPUT - 5 years, 10 months ago

My handwriting is just...bleh...It's kinda bad,really...I'll soon get a handwriting just as good as yours :P just watch...

Yashwanth Manivannan - 5 years, 10 months ago

@Yashwanth Manivannan – All the best :) i hope u get it soon ...

RAJ RAJPUT - 5 years, 10 months ago

I don't quite get why the friction comes first than the tension. The string seems to be tensioned (it is an actual word, right?) and it is also inextensible. My heart says that the string has just as much reason to act than the friction, so what is the deal?

I suggest a slight modification on the figure. If the string wasn't so linear and was, instead, a bit curvy, I would agree that the friction would come first.

Please correct me if I said anything really stupid.

Fernando Tsurukawa - 5 years, 9 months ago

for curvy there is no problem you got it, now suppose there is no friction than F=40 N is applied then tension will oppose it " as box will be having a ability to move " same is this here to have tension in action box will have to be in tendency to move but friction interrupts and tension does not come into play ... hope you got it .... if not ask clearly the point you are not getting

RAJ RAJPUT - 5 years, 9 months ago

Well, I still don't quite get it.

I feel that the last bit of your explanations could be rewritten like this: "(...) to have FRICTION in action, box will have to be in tendency to move but TENSION interrupts and FRICTION does not come into play (...)".

You see, the rewritten sentence makes sense to me, so I couldn't really tell which one is true.

Don't get me wrong, I'm not trying to contest classical mechanics, I just want to understand it.

Fernando Tsurukawa - 5 years, 9 months ago

@Fernando Tsurukawa – YEAH. I know exactly how you feel man, I was trying to understand the same concept intuitively. It's easy to explain if you consider an extreme case.

Imagine a really really heavy box resting on the ground with a string having a little bit of slack in it at the start. If you pull it, what will happen? Nothing, since friction prevents you from moving it! But if you keep pulling, the box will move until the string becomes taut. Only then does tension begin acting.

Another way to think about it is that friction is the gluey force that holds things down to the ground and prevents them from moving laterally. If you want to move an object, you first have to melt the glue (overcome the friction) and then other forces can act on it.

EDIT: I just read your first comment and realized that I had just explained your curvy string thing. The answer to your question is that there is no difference between a straight string and a curvy string since tension is 0 in both cases initially, though they are drawn differently.

Raj Magesh - 5 years, 9 months ago

@Raj Magesh – great explanation same i was trying to explain , and by the way there is difference between curvy string and straight string , just suppose a situation using data of this question where string is taut and external force is 51 N then tension will appear but if with the same force an curvy string is pulled tension will be zero till string is taut and may be full extra force (after friction) is not enough to let the string be taut :) :)

RAJ RAJPUT - 5 years, 9 months ago

@Fernando Tsurukawa – Friction is a self adjusting force, here when force is more than 50 (maximum value of static friction ) then only tension comes into play

RAJ RAJPUT - 5 years, 9 months ago

Which comes first: tension or friction?

1 solution

0 pending reports