Which is greater?
7 1 7 0 or 7 0 7 1
Which one of the two numbers above is greater?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
37 solutions
Moderator note:
Thanks for showing the Binomial Expansion approach.
Log 7071= 71 Log 70= 131.0019608 Log 7170= 70 Log 71= 129.5880844
Log in to reply
your solution has a drawback/ you use a calculator to compute Log71 and log70
Log in to reply
yeah not very insightful, they things is we have been trained to compute haha
@Chew-Seong Cheong How do you think of these solutions
Log in to reply
7 1 = 7 0 + 1 gives me the clue. There must be a way the problem creator thought of when creating the problem. We have to guess it in solving the problem.
Log in to reply
1/X(lnX) is a decresing function for X>e So 1/70(ln70)>1/71(ln71) => 70^71>71^70
Log in to reply
@Bhargav Pavuluri – Doesn't that just imply that 70^70 < 71^71?
Log in to reply
@Franklin Gregory – i think misunderstood what i meant was (lnX)/X
The brilliancy is not only at the beginning of the solution, also the last two steps are neat and elegant.
Notice how @Chew-Seong Cheong drives your attention to the fact that, after applying the binomial theorem, the number 71^70 can be expressed as the sum of 71 terms. It' also pretty easy to spot that each term is lesser or equal than 70^70
Now you just need to realize that 70^71 is the same as 70*(70)^70. It takes (at least to me) a little leap of imagination to see that this is the same as adding 70^70 for seventy times. Since every term of the first sequence (the binomial one, so to speak) is less than 70^70 we got our solution.
It's just beautiful to find such a simple concept as the very definition of multiplication useful to solve a definitely more complex problem.
Thank you sir for sharing this.
I love this way, Sir.
Sorry sir, but can we just predict that 70^71 will have more digits than 71^70?
Therefore 70^71 > 71^70 ?
Thank you :)
Log in to reply
Of course, you can. I believe it is using lo g x . If we are using a calculator for it we must well just use calculator to for the actual values of 7 0 7 1 and 7 1 7 0 .
(70)^71 = (70x70)^70 > (71)^70
Log in to reply
7 0 7 1 = 7 0 ⋅ 7 0 7 0 = ( 7 0 ⋅ 7 0 ) 7 0 = 7 0 1 4 0
Simple logic. ●We have 70^71 and 71^70... ●70^71 = 71 times 70 is present. ●71^70=(70+1)^70=(70^70)+(1^70)=(70 times 70)+(1)=70 times 70 +1(1 added to result of 70^70).. ●So we have 71 times 70 in 70^71 and 70 times 70 in 71^70. ●Hence,70^71>71^70
I have done it using the same exact method....... :-)
Amazing sir
I did similarly
I can tell simplicity is something you do not keep in mind. I don't understand why you would want to work out the long way when there is a way easier way lol...some people
Log in to reply
I actually just keyed in using Python 7 0 ∗ ∗ 7 1 > 7 1 ∗ ∗ 7 0 and then [Enter], and the result was "True". But this did not involve Algebra and not a good solution.
Log in to reply
Lol best answer :),your sense of humour is good :D
That's rude.
That's true. I just found out from looking at different exponential comparisons (such as this one) that the smaller number to the power larger number is larger than the larger number to the smaller number.
Log in to reply
doesn't work for 2 and 3
Log in to reply
@Wael Radwan – Doesn't have to work for all numbers. The question was about 70 and 71. If this was asking about 2 and 3 then yes you are correct. But otherwise not really relevant.
@Wael Radwan – Are 2 an 3 the only exceptions?
Log in to reply
@Jess Doe – that's a good question to ask ..
7 1 7 0 7 0 7 1
7 1 ln ( 7 1 ) 7 0 ln ( 7 0 )
Consider function f ( x ) = x ln ( x ) and the derivative is x 2 1 − ln ( x ) since we have this we know that when x > e it's a decreasing function.
Hence, when the x value increase the value of function decrease.
So,
7 1 ln ( 7 1 ) < 7 0 ln ( 7 0 )
then
7 1 7 0 < 7 0 7 1
Best proof as it can be applied to analyse when a^b > b^a
This is a nice way to think!
😕😕I don’t get it🤔🤔
beautiful way of using calculus
Beautiful. I used log function but no calculus. Just some numerical analysis.
Putting 2 and 3 into your analysis for a and b respectively, your proposition falls utterly. @ABHISHEK JOHN MARTIN
Log in to reply
Yes, it does. But that is not because my method is wrong. Rather I think you don't seem to understand what I wrote. It, generally, falls if you substitute 2 numbers that are on the opposite side of "e" since we have no right to conclude anything using this method. So, what you did is basically substitute what can go wrong and show that it is wrong.
Logs had different bases in last step How did you remove the bases and compare?
Log in to reply
He converted the logarithmic notation to exponential form It follows this basic rule:
x y = a T h e n , l o g x a = y
Log in to reply
If he did that, we would get 70<71 in the last step. Instead he did something, which makes no sense after circling around a lot. After the first 2 lines you can skip directly to the last 2. Last step is basically going from the logaritmic form of 70<71 straight to the solution with no justification. Of course the solution is true, but why and how that is conected to 70<71 is not shown. This is a solution with a lot of unnecessary math, which then jumps straight to the solution as if to confuse a potential examiner he gets it...
Circular reasoning
it seems like in the last step you have proven 70<71... can you explain how you got to comparing the powers?
In the second last step, you went back to the second step of the problem which says Log X base 71 = 70 and Log X' base 70 = 71. So we already know Log X base 71 < Log X' base 70. Why do you need so much of derivation for that??
Hi Sushil Kumar, if you use this logic, you can prove that 1^1000 is greater than 1000^1. Hope you understand..
Log in to reply
The case cannot be done with 1 because something base 1 in logarithm is 0 .
Log in to reply
No, because it's undefined. logbase1(x)=ln(x)/ln1=ln(x)/0
Kulmar's logic is jumping from a<b to b^a<a^b, which is wrong. It a logical leap, which proves nothing. This by itself is enough.
It also happens to be wrong in some cases indeed: When a, b are in (0,e]. For example, 3^4>4^3, but 2^e<e^2
incorrect sol.
how did you change the inequality signs
Log in to reply
By the logic above, the steps should follow substituting 2 and 3 for 70 and 71 respectively. But the don't because the last step is faulty. Comparing logs in different bases is apples and oranges.
Suppose 7 1 7 0 > 7 0 7 1 ⇒ 7 1 7 0 > 7 0 ⋅ 7 0 7 0
We can rewrite this inequation as
( 7 0 7 1 ) 7 0 > 7 0
Or...
( 1 + 7 0 1 ) 7 0 > 7 0
The expression on the left is now on the form
( 1 + x 1 ) x
Which we know is never greater than the euler constant (2.71828) for increasing values of x, and thus can't be greater than 70. So it turns out then that the opposite is true ( 7 0 7 1 > 7 1 7 0 )
very well done, Best explanation so far.
My favorite explanation so far. Thanks.
your solution is better than the top rated solutions,now i understood clearly.
Bravo! I have got a similar solution
We can solve this using a Taylor Expansion. First we consider the following Taylor Expansion of ( 1 − x ) n ≈ 1 − n x , where x ≪ 1 . It follows then that
( 7 1 ) 7 0 = ( 7 0 + 1 ) 7 0 = 7 0 7 0 ( 1 + 7 0 1 ) 7 0 ≈ 7 0 7 0 ( 1 + 7 0 7 0 1 ) = 7 0 7 0 × 2
Concerning the other term,
7 0 7 1 = 7 0 7 0 × 7 0 1 = 7 0 7 0 × 7 0 .
Thus,
7 1 7 0 < 7 0 7 1 .
Solved like a true Physicist.
however don't you feel we must not use approximations to solve such problems...
Log in to reply
On the contrary, this is the perfect problem to use an approximation. This such problem asked which of two terms is greater than the other. It did not ask for exact values.
Althought he used an approximation, this is a real mathematical identity: I am too lazy to format, so e= epsilon > 0 but less than 1 and very small.
Hence, (1 + e)^n >= 1 + n*e
Where n is any positive integer (including 0).
Which can be shown through mathematical induction as follows:
a) for n=0, we have that 1=1 b) now, if we assume that the nth case is true, we must induce the n+1 case
Hence, (1+e)^n(1+e) = (1+e)^(n+1) >= (1+n e)(1+e) = 1 + e + n e + n (e^2) = (1 + (n+1) e) + n*(e^2)
But, we must hand the last term:
Since e > 0 and very small anf since n>=0, we can see right away that n*(e^2) >= 0
==> (1 + (n+1) e) + n (e^2) >= 1+(n+1)*e
Hence, (1+e)^n >= 1 + ne is true for all integers n>0 and for all epsilon, e > 0 and very small.
Now, back to the problem at hand:
Consider 71^70:
71^70 = (70 +1)^70 = (70^70)(1+(1/70))^70 So, the second multiplicative term takes on our identity where e=(1/70) and n = 70
Which means that 71^70 >= (70^70)(1 + 70*(1/70)) ==>
==> 71^70 >= (70^70)(70)((1/70) + (1/70)) = (70^71)(2e) > (70^71)*e
Hence, since 1 > (70^71)*e/(71^70)
But, we argue since e is very small and that since neither (70^71) nor (71^70) are small that (71^70)* (very large) > (70^71)
So, (70^71) > (71^70)
Let's say 71 = 70*X
71^70 = 70^70 * X^70
Multiply with 70 on both side
71^70 * 70 = 70^71 * X^70
71^70 / 70^71 = X^70 / 70
Now if, X^70/ 70 >1 then 71^70 is more else 70^71 is more
Approx Calculation for X is 1.01. So X^70 will turn out to be approx = 1 . Hence X^70/ 70 = 1 / 70 (approx.) < 1
So 70^71 is more :). Hope this was a simple solution and easily to explain to others.
This how I solve the majority of problems:
take a small sample data:
2
3
=
8
3
2
=
9
4
3
=
6
4
3
4
=
8
1
5
4
=
6
2
5
4
5
=
1
0
2
4
By induction we can reason that for n > 2
n
n
+
1
>
(
n
+
1
)
n
T
h
e
r
e
f
o
r
e
:
7
0
7
1
>
7
1
7
0
Moderator note:
This is incomplete. You have not proved that it's true for all integer n .
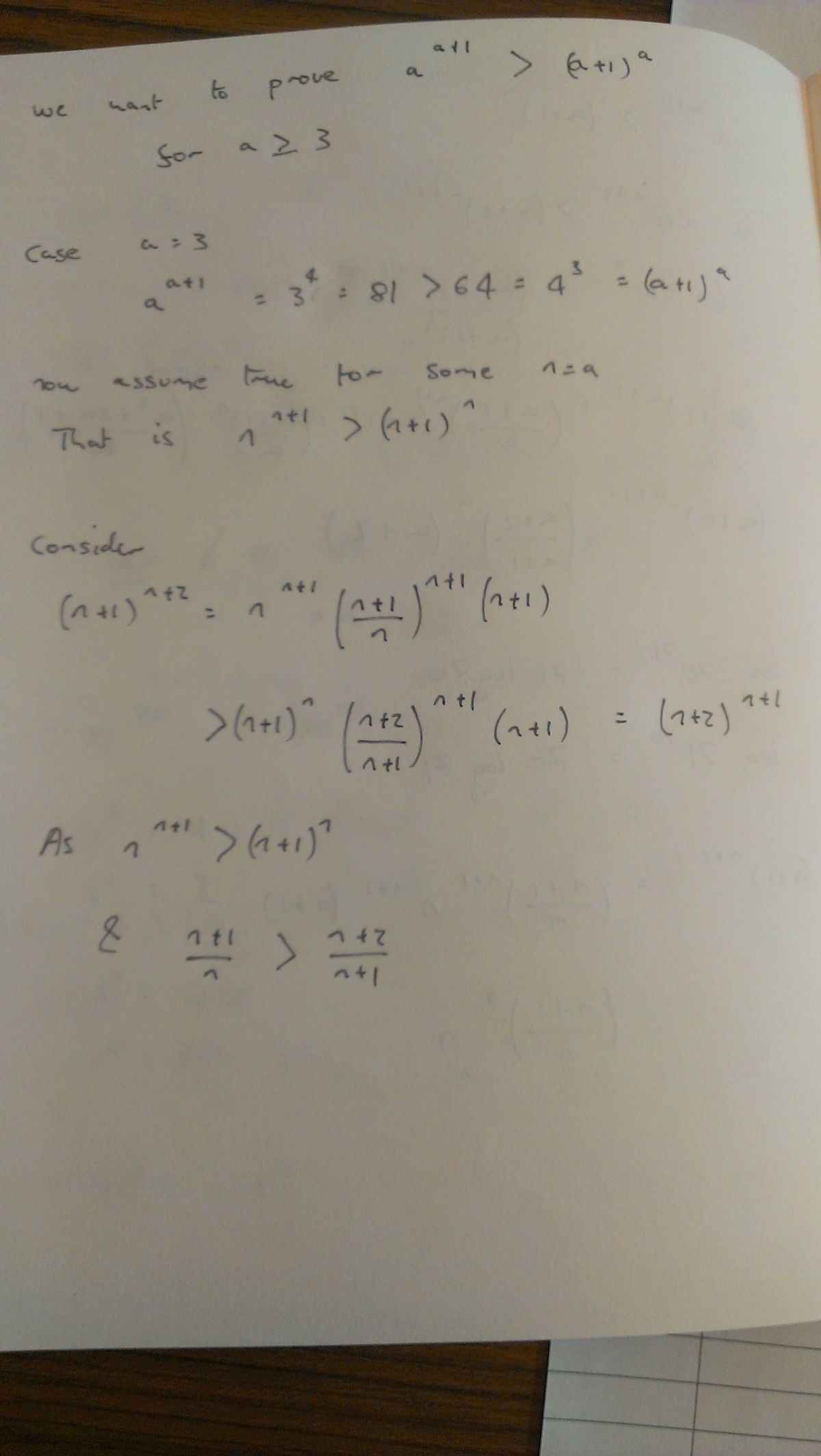
"Challenge Master note: This is incomplete. You have not proved that it's true for all integer N."
Don't have to prove that this is true for all integer N. Just have to prove that there is an ever growing expansion between results. Plus note, that any counter example to this theory exists is < 3.
Log in to reply
If there is an ever growing expansion between results how can it not be true for all ints after a certain one? The only way to prove there is not any counter example >=3 is, well...to prove it!
Here's a quick three-step method that works for problems of the same type with sufficiently large numbers.
-
Consider the ratio 7 0 7 1 7 1 7 0 .
-
Rewrite the ratio as 7 0 1 . ( 1 + 7 0 1 ) 7 0 .
-
Recognize e (~ 2.71828) is an upper-bound of ( 1 + 7 0 1 ) 7 0 , since e = lim n → ∞ ( 1 + n 1 ) n and the sequence is monotonically increasing.
It now becomes clear that 7 0 7 1 7 1 7 0 < 7 0 e < 1 , implying 7 1 7 0 < 7 0 7 1 . QED.
Took me a minute going from ( 1) to ( 2), but 100% yes.
( 1) = (71/70)^70 * (1/70) = ((70 + 1) / 70)^70 * 1/70 = ( 2)
The fact that (1+1/n)^n is increasing is not 100% obvious, but it is a standard fact.
Log in to reply
Indeed, such a statement is not trivial, and I assumed the reader was familiar with the sequence. Here's a full proof of that claim. The argument is conducted via contradiction.
Suppose there exists a natural number m such that the following holds:
( 1 + m 1 ) m ⩾ ( 1 + m + 1 1 ) m + 1 .
Then, manipulation of the inequality shows that...
1 ⩾ ( 1 + m 1 ) m ( 1 + m + 1 1 ) m + 1
1 ⩾ ( m m + 1 ) m ( m + 1 m + 2 ) m + 1
1 ⩾ ( m m + 1 m + 1 m + 2 ) m ⋅ m + 1 m + 2
1 ⩾ ( m m + 2 ) m ⋅ m + 1 m + 2 .
Herein lies the contradiction.
Call A = m m + 2 and B = m + 1 m + 2 . Then, the inequality found above reads 1 ⩾ A m ⋅ B .
Certainly, A > 1 , and so too is any power of A , namely A m . Moreover, B > 1 . Thus, one expects A m ⋅ B > 1 , yet this contradicts the inequality found above.
Therefore, for each natural number m , it must be true that ( 1 + m 1 ) m < ( 1 + m + 1 1 ) m + 1 . The sequence is strictly monotonically increasing by definition. QED.
Log in to reply
The double-reciprocal is off here... Assuming that this proof is supposed to precede knowledge of calculus and logarithms, the only approach I can think of ends up using the Binomial Theorem and a comparison with a Geometric series. I thought I remembered this being a sticky problem, and the more I look at it, the more I feel like my memory was right on that. It's probably proved early in Rudin's text... I don't want to write up what I have because it's probably not the cleanest or even 100% correct...
Log in to reply
@Matthew Bond – http://math.stackexchange.com/a/167869
Bernoulli's Inequality can probably be proved by calculus without logarithms, so it's still elementary enough that it's not cart-before-the-horse. There's probably a Binomial Theorem trick for that one too.
I only bring all this up because the difference between "well-known" and "obvious" is often pretty big, and people less experienced might not know which is which.
great approach
Why m m + 1 m + 1 m + 2 = m m + 2 ?
m m + 1 m + 1 m + 2 = m + 1 m + 2 ⋅ m + 1 m
Log in to reply
@Timothy Tsvetkov – Sadly, it's a mistake, so the proof falls short. You need to use Matthew's approach.
divide both side by 7^70
(71/70)^70 vs 7
It helps to look at the general case.
(n+1)^n < n^(n+1) for all n>~2.29317, which is the solution to the equation (n+1)^n = n^(n+1)
Here n = 70, which is much larger than the value of ~2.29317
- 71^{70} = (70+1)^{70}
- 70^{71} = (70)^{(70+1)}
From 2, 70^{70}x70^{1}, therefore will be greater.
Please correct me if i''m wrong :)
"1^t = 1 (t € R)" 71/70 ~= 1 (71/70)^70 = a small number (71/70)^70<70 of course 71^70<70^70 * 70 71^70<70^71
take log on both sides. 71 log 70 and 70 log 71 now log x < x now, 71 > 70 log 70 < log 71 but multiplied together 71 log 70 > 70 log 71 since log x has smaller effect than x .
This is on the right track, but needs a little more polish. The idea is that 70 log70 = 70 log70, and to see how the quantity changes as one of the 70s changes.
Let <> stand for the unknown inequality, and >< its opposite if needed.
Consider a log(a + e) <> (a + e) log a
a = 70, e = 1. The important features are that a>1, and e>0.
Equality holds if e=0, but for e>0, both sides are positive with positive derivative. Treating e as the only variable, the LHS has derivative (that is, d/de) equal to a/(a +e), and the RHS has derivative log a. So as e increases, the LHS increases more slowly. In fact, the RHS grows more than log a times as fast!
a log (a + e) < (a + e) log a, and so 70 log(71) < 71 log(70)
You can be more accurate, too. The LHS could have grown log times as fast and still lost, because a/(a+e) < 1. We could prove that:
a log (a + e log a) < (a + e) log a.
So we even have
70 log (70 + log70) < 71 log 70 (70 + log 70) ^ 70 < 70 ^ 71. (The LHS is bigger than 71^70)
Log in to reply
I expanded this a bit and clarified a couple things as a separate solution, if anyone's interested. What I wrote above is now a little muddy and has a couple of typos. (Confusingly, I also used the character "e" as a variable, which is really bad practice.)
log 71 > (log 71 - log 70) x 71, so 70 ^ 71 is greater
Is this a valid calculation?
Of course, the easiest solution is to plug both directly in calculator. You will get difference of 9.6579e130 approximately.
However, it can be proven, that ∀ x , a , w h e r e x > a > e , a x > x a
Therefor 7 0 7 1 > 7 1 7 0
Let's just say this: Powers and exponentials get big. The power and base are not negative, or 1, but in fact REALLY BIG. This means the power can easily take over, even if the base is one less! Use your intuition with this one( or, if you REALLY want, your calculator)
We know that a a + 1 & ( a + 1 ) a that a a + 1 > ( a + 1 ) a such that a is a integer & a > 2 so 7 0 7 1 > 7 1 7 0
Write the fraction 7 0 7 1 7 1 7 0
then scompose 7 0 7 1 = 7 0 7 0 ∗ 7 0
then we collect ( 7 0 7 1 ) 7 0 ∗ 7 0 1
noticed that 7 0 7 1 ≈ 1 . 0 0
so 7 0 7 1 7 1 7 0 = ( 7 0 7 1 ) 7 0 ∗ 7 0 1 ≈ 7 0 1 < 1 .
If we have a fraction less than one the denominator is bigger than the numerator so the answer is 7 0 7 1
From the following evaluations it can be infered that 7 0 7 1 > 7 1 7 0 as the values on the left of the inequality sign are increasing faster than those on the right of the inequality sign \begin{array}{*{20}{l}} {{0^1} < {1^0}}&{{\text{as }}0 < 1} \\ {{1^2} < {2^1}}&{{\text{as }}1 < 2} \\ {{2^3} < {3^2}}&{{\text{as }}8 < 9} \\ {{3^4} > {4^3}}&{{\text{as }}81 > 64} \\ {{4^5} > {5^4}}&{{\text{as }}1\,024 > 625} \\ {{5^6} > {6^5}}&{{\text{as 1}}5\,625 > 7\,776} \\ {{6^7} > {7^6}}&{{\text{as }}279\,936 > 117\,649} \end{array}
Take small numbers do calculations e.g. 3 power 4 is equal to 81 and 4 power 3 is equal to 64 This way small number with greater power comes out to be larger number so 70 base power 71 is larger than 71base power 70.
7 1 l n 7 0 7 0 l n 7 1 = 0.989
meaning the denominator has a higher value. thus 70^71 has the larger value
It can be easily derived using induction
Clearly 70^71 is greated than 71^70 as 70 is to a larger power.
What about 0 1 < 1 0 or 1 2 < 2 1
We know that if a<b de have ln(a)<ln(b), So, ln(71^70)=70ln(71)=70ln(70) + 70ln(71/70)
And ln(71/70) is very close to zero On the other hand de have ln(70^71)=71ln(70)=70ln(70)+ln(70)
Then ln(70)>70ln(71/70) So, ln(70^71)>ln(71^70) And, 70^71>71^70
Well.... 2^8 is greater than 8^2....therefore 70^71 is greater than 71^70
Well ... 1^2 is less than 2^1 ... therefore 70^71 is less than 71^70 or ... 0^1 is less than 1^0 ... therefore 70^71 is less than 71^70 same reasoning but wrong conclusion
Let's try to solve this using calculus.
7 1 7 0 ? 7 0 7 1
7 1 7 1 1 ? 7 0 7 0 1
Now, let's look at the function n n 1 .
Let's differentiate it.
d n d n n 1 = d n d e l n ( n n 1 ) = d n d e n l n ( n ) = ( d n d n l n ( n ) ) e n l n ( n ) = n 2 1 − l n ( n ) e n l n ( n ) = l n ( n e ) n n 1 − 2
Which is negative iff n > e .
This means that n n 1 is strictly decreasing when n > e which implies that 7 1 7 1 1 < 7 0 7 0 1 which in order implies that 7 1 7 0 < 7 0 7 1 .
Thus, 7 0 7 1 is greater of these 2 numbers.
(This also proves that n m < m n , if e < m < n )
Moderator note:
Good rigorous approach to tackling this problem.
I don't know what you guys are thinking but I just thought about what calculators did when there were too many zeros
71^70 = X so 70log71=log X hence 10^129.588 =X
70^71 =Y so 71log70= log y hence 10^131.0019608 =Y
Y>X
(1+1/n)^n-->e when n is toward infinity provided n is a positive integer, it will always smaller than e (71/70)^70<e<70 (71^70)/(70^70)<70 71^70<70^71
71^70=(70+1)^70=70^70+141
70^71=70^70 70=70^70+(70^70) 69
(70^70)69>141
70^71>71^70
If we have y x and x y when x > y
Then y x > x y
Only if {x,y} = 1
And {x, y} ∈ R
But when:
x = 3 ∨ y = 2 → y x < x y
x = 4 ∨ y = 2 → y x = x y
Is it bad that I did this in my head and have no logic behind it? In my head 70^71 > 71^70 is the same as 1 + 1 = 2. Sure I could write some crazy theorem to prove it or I could just know it is true and leave it at that.
70^71=[70^(71/70)]^70=(74.38...)^70 > 71^70
I figured I would post my reply to a solution that I saw in this thread. It was basically a correct idea using intuition about growth rates, but it wasn't 100% spelled out.
Let <> stand for the unknown inequality, and >< its opposite if needed.
71^70 <> 70^71
Well, we know that 70^70 = 70^70, and we increase one number on each side by one. Which grows more?
The question is (a+E)^a <> a^(a+E).
a = 70, E = 1. The important features are that a > e = 2.718... , and E>0.
Log helps. (You can use log 10, but the "pure math" convention is log e, sometimes written as ln)
The question, then, is a log(a+E) <> (a+E) log(a)
Equality holds if E=0, but for E>0, both sides are positive. Treating E as the only variable, the LHS has derivative (that is, d/dE) equal to a/(a +E), and the RHS has derivative log a. So as E increases, the LHS increases more slowly. In fact, the RHS grows more than (log a) times as fast! log a > 1 > a/(a+E), since a > e and E>0.
a log (a + E) < (a + E) log a, and so 70 log(71) < 71 log(70)
You can be more accurate, too. The LHS could have grown (log a) times as fast and still lost the growth race, because a/(a+E) < 1. We could prove that:
a log (a + E log a) < (a + E) log a.
So we even have
70 log (70 + log70) < 71 log 70, (Calculator says: 301.519... < 301.643...)
or
(70 + log 70) ^ 70 < 70 ^ 71. (The LHS is bigger than 71^70) (big numbers...)
In other words, (since log(70) = 4.248... )
(74.248...)^70 < 70^71
I probably should've used 70 and 1 instead of a and E all along for simplicity, but I ended up saying everything twice instead. I don't think I'll change it now, though.
Yikes, why did I name a variable e? I went back and changed it to capital E so it doesn't look like base-e, which is actually an important number here.
just follow this 2^3 < 3^2
ur method is brutally wrong
Shouldn't that imply that 71^70 > 70^71?
this is wrong because 3^4>4^3........
Yah we can do by binomial theorem too. But my friend have already done that! So I have a different approach. Let 71 =2, and 70 =2 so we have 2^70and 2^71 which is bigger we know! Just fun!
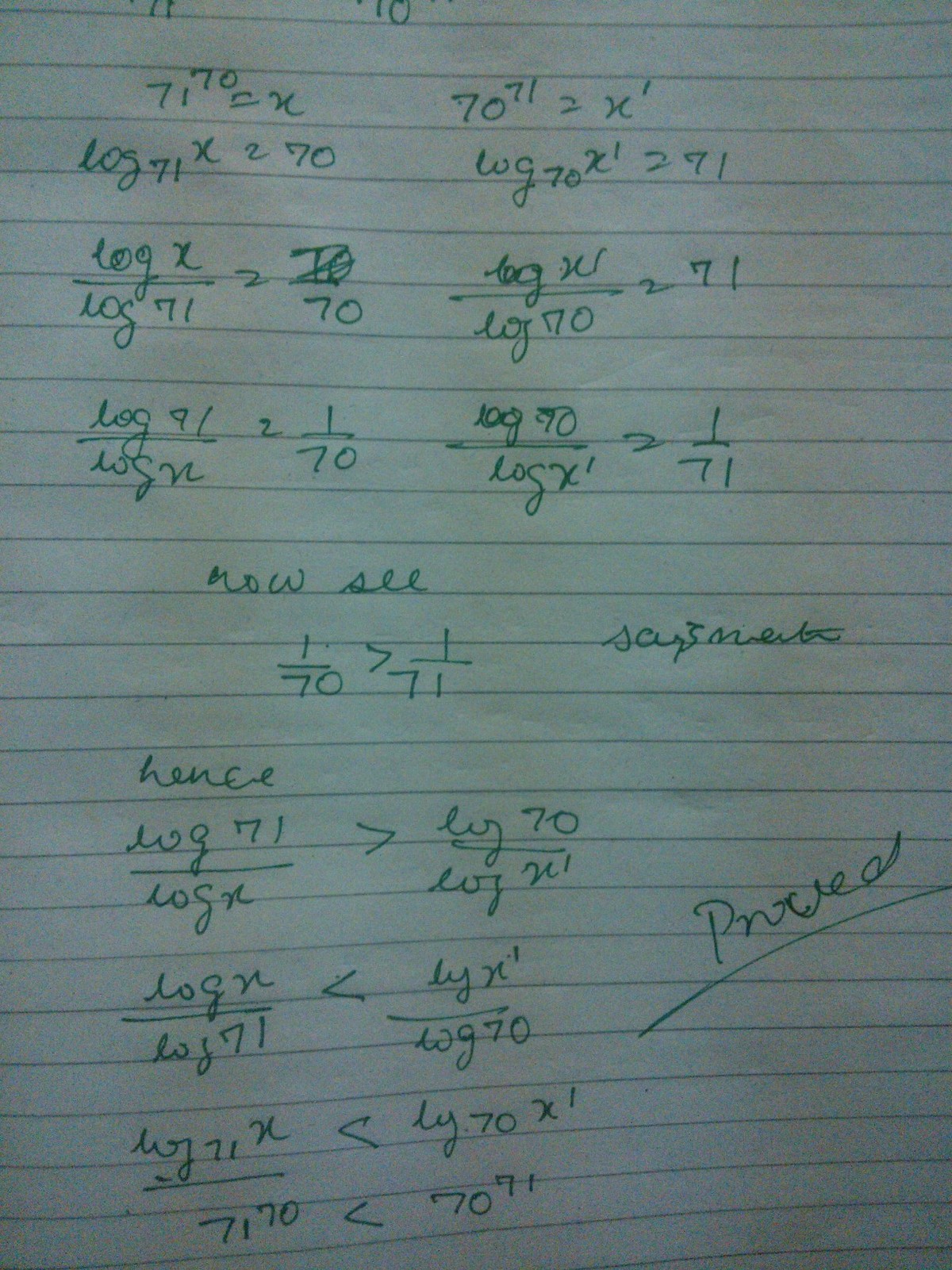
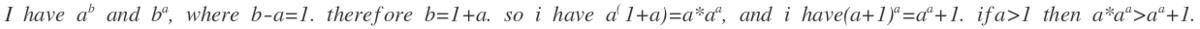
We can use binomial expansion to help compare these two numbers:
7 1 7 0 = ( 7 0 + 1 ) 7 0 = 7 0 7 0 + 7 0 ( 7 0 6 9 ) + 2 7 0 ˙ 6 9 ( 7 0 6 8 ) + 2 ˙ 3 7 0 ˙ 6 9 ˙ 6 8 ( 7 0 6 7 ) + . . . + 1 [ 7 1 terms ] = 7 0 7 0 + 7 0 7 0 + 2 6 9 ( 7 0 6 9 ) + 2 ˙ 3 6 9 ˙ 6 8 ( 7 0 6 8 ) + . . . + 1 < 7 0 ( 7 0 7 0 ) = 7 0 7 1
⇒ 7 0 7 1 > 7 1 7 0