Which portion has the largest area?

Divide the left and right sides of the yellow region into $3$ congruent parts, the left and right sides of the blue region into $2$ congruent parts, and draw parallel lines through these points to make congruent triangles, as follows:

The yellow region has $9$ triangles, the blue region has $16$ triangles, and the red region has $11$ triangles, so the blue region has the largest area.

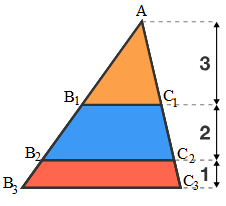
Note that $\triangle AB_1C_1$ , $\triangle AB_2C_2$ , and $\triangle AB_3C_3$ are similar triangles. Therefore, their areas are directly proportional to the square of their respective linear dimensions. Let the area of $\triangle AB_1C_1$ be $3^2 A = 9A$ . Then:

$\begin{cases} [AB_1C_1] & = A_{\color{#EC7300}\text{orange}} = 9 A \\ [AB_2C_2] & = A_{\color{#EC7300}\text{orange}} + A_{\color{#3D99F6}\text{blue}} = 25 A & \implies [AB_2C_2]-[AB_1C_1] = A_{\color{#3D99F6}\text{blue}} = 16 A \\ [AB_3C_3] & = A_{\color{#EC7300}\text{orange}} + A_{\color{#3D99F6}\text{blue}} + A_{\color{#D61F06}\text{red}} = 36 A & \implies [AB_3C_3]-[AB_2C_2] = A_{\color{#D61F06}\text{red}} = 11 A \end{cases}$

Blue portion, therefore has the largest area.

Let $area_{whole}=m$

$area_{orange}=\frac{m}{4}=\frac{9m}{36}$

$area_{blue+orange}=\frac{25m}{36}$

So, $area_{blue}=\frac{16m}{36}$

So, $area_{red}=area_{whole}-area_{blue}-area_{orange}=\frac{11m}{36}$

So, $Area_{blue}>Area_{red}>Area_{orange}$

Related proof : Areas of similar triangles

The ratio of area of similar triangles is equal to the ratio of square of their corresponding sides.

   O=area of Orange
   B= area of Blue
   R=area of Red  

 1).  (3/5)^2=O/(O+B)

 2).  (O+B)/(O+B+R)=(5/6)^2

Solving ,we get B:O:R=16:9:11

Clearly. Blue has the largest area.