Which topic does it belong??
If A 1 , A 2 , . . . , A n be the vertices of a n - sided regular polygon such that: A 1 A 2 1 = A 1 A 3 1 + A 1 A 4 1 Then find the value of n
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A Brilliant approach :)
Easy Problem! I solved It by using Complex Number's !
Trick is that our answer is independent of reference Side Length of Polygon , So Let the vertex as the n' th root's of unity ! where Origin is cir-cum centre of origin
So Vertex is A k ≡ ( e i n 2 ( k − 1 ) π )
A 1 A k = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − e i n 2 ( k − 1 ) π ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ 1 − cos n 2 ( k − 1 ) π − i sin n 2 ( k − 1 ) π ∣ ∣ ∣ ∣ ∣ A 1 A k = 2 sin n ( k − 1 ) π ∣ ∣ ∣ ∣ ∣ sin n ( k − 1 ) π − i cos n ( k − 1 ) π ∣ ∣ ∣ ∣ ∣ A 1 A k = 2 sin n ( k − 1 ) π ∵ A 1 A 2 1 = A 1 A 3 1 + A 1 A 4 1 sin n π 1 = sin n 2 π 1 + sin n 3 π 1 ( S a y n 2 π = θ ) sin 2 θ 1 − sin 2 3 θ 1 = sin θ 1 ⇒ sin 2 θ = sin 2 3 θ 2 θ + 2 3 θ = π θ = 7 2 π = n 2 π n = 7
Q.E.D
nice solution!I also used the complex number approach to solve this before posting it.
Since Reply on Lavisha Parab is not working I am writing here. I greatly admire the approach both of you have taken. In both cases the approaches are useful for solving other problems. Congratulations to both of you.
Cool ! I used Trignometry and expressing side in terms of Circumradius ! But Your Approach is awesome !
An iitjee complex no.s and solution of triangles problem.
Log in to reply
So in which Year it is asked by IIT's ?
Log in to reply
Solved it a while ago so i don't remember the year specifically.I'll check and let you know .
Log in to reply
@Gautam Sharma – Just googled it!.It was asked in 1994 , 4 marks problem.
Log in to reply
@Gautam Sharma – Thanks! So It Mean's
IIT 4 Marks question=280 Point's on Brilliant ! That is insane ! Lol'z
Log in to reply
@Karan Shekhawat – Yeah ! its really cool.Hats off to jee.
Log in to reply
@Gautam Sharma – Yes , Old IIT JEE's Paper's ( In 90's and before ) are Really Good and tough ! But From Present Day's I have no respect for JEE Paper's , They now only focus on time constrained not much on difficulty Level . Any way are u in 12th or 11th ?
Log in to reply
@Karan Shekhawat – I am in 11th. I have respect for jee papers because limiting the time increases the difficulty level to an higher extent . In old papers questions were not really asked on basic concepts ,they used to have complex calculations and simple applications for formula but now they are shifting there view to concepts and which gets really hard and confusing sometimes and difficulty level is also not that down ,actually i think its better than ever because when i attempt previous years questions I am able to solve subjective old problems (just hold the pen and smoothly fill the pages) but sometimes I have to spend a little more time thinking about concepts used in objectives question(recent years 2006-2014).Different types of questions Integer type,matrix match,fill ups ,comprehension types And so called multicorrect make it really difficult. (i have to admit multicorrect are really difficult).
Btw you are in 12th right?
Log in to reply
@Gautam Sharma – Well I'am in 13th !Everyperson's have different Views , But Yes I agreed That Multiple correct Need's very Precise Knowledge ! That was The main reason that JEE 2014 Paper-1 is comparitiely difficult due to 50% multiple correct Question . :) And Personally I feel that we are going to be engineer not an fast bowler , So In my views speed should not be cretiria for judjing a person's ability ! Old Day's IIT's beleive in this concept , but due to excessive compettion and more no: of student's They start Objective .
Log in to reply
@Karan Shekhawat – They want to test us under every condition in this case they test us how we perform in exam pressure created due to time limit.
this was also asked in inmo
Hi @Deepanshu Gupta , nice solution :)
Can you help me out by suggesting how to become better at solving questions from complex numbers and from Oscillations and Waves ? These can be considered as my weakest areas in Maths and Physics .
Thanks for the same :)
Log in to reply
Thanks ! Well u r already an In genius Mind , and I like your Problem Solving skill's . And Yes, I love complex numbers , And as I'am also an student , So it is difficult to suggest anything about it (Specially Person Like u ) , But Yes I can Tell you that what had I tied and try to do in complex number's : Truly Speaking my Interest in Complex number is developed while studying of Alternating Current in physics , Complex number technique which was taught to me by my Professor in solving AC cct's fascinates Me Very much . Since Complex number is officially Taught to me in Last few day's , So from beginning of this year I always try to solve Problem By using complex number's . Since My Math Teacher's say's that He Solved approx 40% of IIT JEE paper in his JEE day's using complex number . This inspiration is really good source for me . From Then to till Now while studying any Problem , then I firstly Think whether I use complex number's or Not .
So I Only thing which can I recommend You is " Think Complex , Love complex, and try to Kill prob's by complex . You will Surely get Expertise in it .
It may sound odd , But If you really want To Expertise and developed interest in Comp. No: then I recommend You to read small History of Complex Number's . Like Origin of complex Number's , what/How [ Wow :) ] are Discovery's in it . I Have Tried This Technique in many chapter's which doesn't fascinates me initially . In NCERT in starting and in ending of chapter's Summery was given for each Topics. Try This believe me A new Positive energy and Interest will develope in you , which definetly Help to Sharp your Skill's (which is already sharpened in You )
For Wave's , The Important thing is that , how carefully You Read the Theory . Becoz there are several small-small thing's in this section , which need's carefull attention . Like as : Velocity of wave's in progressive wave v=sqrt(T/\(\mu )) is defined w.r.t Medium (Means We have to consider Pseudo forces if medium is accelerating relative to our reference frame) Similarly for Doppler's efect formula's are derived w.r.t ground frame . etc.
So I suggest you To first read theory very carefully , and then do problem's which were really very-very easy Upto J EE level , even Olympiad's level too. Have faith in yourself , You will suerly Excel in it. Believe me you are ingenious ! Sorry If I bored You ! ⌣ ¨
Log in to reply
No dude, I really appreciate your interest in helping me out . Yeah I'll definitely give a thorough reading to all chapters as you suggested :) Also after reading this I certainly feel more confident than before, I guess that's the expertise of an expert at play .
I was actually a bit scared for Physics since I don'5 have a natural likening for it, but after reading your comment I feel good :)
You really appreciate me a lot, but please don't forget that you are my senior and superior to me in terms of knowledge and I'll always respect you for that .
Anyways, thanks for your advice and Best of Luck for JEE !!!
Log in to reply
@A Former Brilliant Member – Ur welcome Bro ! and Same to you Best of luck ! ⌣ ¨
Anti math way = use geogebra
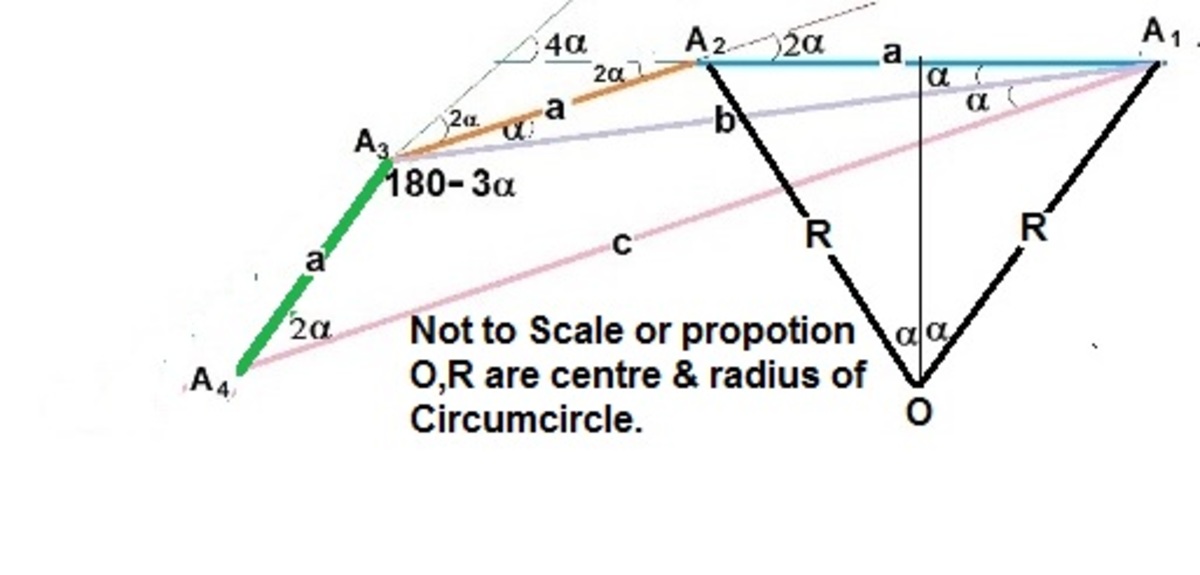 Note the relation of all angles to
α
a
n
d
v
a
r
i
o
u
s
i
s
o
s
c
e
l
e
s
t
r
i
a
n
g
l
e
s
.
Let n be the number of sides.
2
α
=
n
3
6
0
∴
α
=
2
n
3
6
0
.
.
.
.
.
(
1
)
.
The figure shows various angles formed between three sides of a n-gon.
l
e
t
a
=
A
1
A
2
,
b
=
A
1
A
3
,
c
=
A
1
A
4
.
A
p
p
l
y
i
n
g
S
i
n
L
a
w
t
o
△
A
1
A
3
A
4
,
a
S
i
n
α
=
b
S
i
n
2
α
=
c
S
i
n
3
α
∵
S
i
n
(
1
8
0
−
3
α
)
=
S
i
n
(
3
α
)
A
1
A
2
1
=
A
1
A
3
1
+
A
1
A
4
1
⟹
a
1
=
b
1
+
c
1
a
S
i
n
α
=
b
S
i
n
2
α
=
c
S
i
n
3
α
⟹
1
=
S
i
n
α
1
∗
(
S
i
n
2
α
1
+
S
i
n
3
α
1
)
.
.
(
2
)
F
r
o
m
(
1
)
α
=
2
n
3
6
0
.
B
e
l
o
w
w
e
s
e
e
α
f
o
r
d
i
f
f
r
e
n
t
n
.
:
−
n
=
5
→
α
=
3
6
.
.
.
.
n
=
6
→
α
=
3
0
.
.
.
n
=
7
→
α
=
2
5
.
7
1
.
.
.
.
n
=
8
→
α
=
2
2
.
5
.
.
.
.
F
r
o
m
(
2
)
L
e
t
f
(
α
)
=
S
i
n
α
1
∗
(
S
i
n
2
α
1
+
S
i
n
3
α
1
)
Solve this fuction through calculator, graph in graphing calculator
or otherwise for values given above so that
f
(
α
)
=
1
.
T
h
a
t
g
i
v
e
s
n
.
f
(
2
5
.
7
1
)
=
1
.
S
o
n
=
7
.
A
s
n
i
n
c
r
e
a
s
e
s
s
o
d
o
e
s
f
(
α
)
.
Note the relation of all angles to
α
a
n
d
v
a
r
i
o
u
s
i
s
o
s
c
e
l
e
s
t
r
i
a
n
g
l
e
s
.
Let n be the number of sides.
2
α
=
n
3
6
0
∴
α
=
2
n
3
6
0
.
.
.
.
.
(
1
)
.
The figure shows various angles formed between three sides of a n-gon.
l
e
t
a
=
A
1
A
2
,
b
=
A
1
A
3
,
c
=
A
1
A
4
.
A
p
p
l
y
i
n
g
S
i
n
L
a
w
t
o
△
A
1
A
3
A
4
,
a
S
i
n
α
=
b
S
i
n
2
α
=
c
S
i
n
3
α
∵
S
i
n
(
1
8
0
−
3
α
)
=
S
i
n
(
3
α
)
A
1
A
2
1
=
A
1
A
3
1
+
A
1
A
4
1
⟹
a
1
=
b
1
+
c
1
a
S
i
n
α
=
b
S
i
n
2
α
=
c
S
i
n
3
α
⟹
1
=
S
i
n
α
1
∗
(
S
i
n
2
α
1
+
S
i
n
3
α
1
)
.
.
(
2
)
F
r
o
m
(
1
)
α
=
2
n
3
6
0
.
B
e
l
o
w
w
e
s
e
e
α
f
o
r
d
i
f
f
r
e
n
t
n
.
:
−
n
=
5
→
α
=
3
6
.
.
.
.
n
=
6
→
α
=
3
0
.
.
.
n
=
7
→
α
=
2
5
.
7
1
.
.
.
.
n
=
8
→
α
=
2
2
.
5
.
.
.
.
F
r
o
m
(
2
)
L
e
t
f
(
α
)
=
S
i
n
α
1
∗
(
S
i
n
2
α
1
+
S
i
n
3
α
1
)
Solve this fuction through calculator, graph in graphing calculator
or otherwise for values given above so that
f
(
α
)
=
1
.
T
h
a
t
g
i
v
e
s
n
.
f
(
2
5
.
7
1
)
=
1
.
S
o
n
=
7
.
A
s
n
i
n
c
r
e
a
s
e
s
s
o
d
o
e
s
f
(
α
)
.
After getting (2) you may follow Lavisha Parab 's method, or use calculator.
Lavisha Parab 's solution is a better one, but I have given this to show a slightly different approach
.
after having 2 amazing solutions from my friends i have 1 more method..... ∠ ( A 1 A 2 A 3 ) = n ( n − 2 ) π A 1 A 3 = A 2 A 4 = 2 a cos n π n o w , A 1 A 2 ∗ A 3 A 4 + A 2 A 3 ∗ A 1 A 4 = A 1 A 3 ∗ A 2 A 4 a 2 + A 2 A 3 ∗ A 1 A 4 = ( 2 a cos n π ) 2 A 1 A 4 = a ( 4 cos 2 n π − 1 ) n o w , A 1 A 2 1 = A 1 A 3 1 + A 1 A 4 1 2 cos n π [ 4 cos 2 n π − 1 ] = 4 cos 2 n π − 1 + 2 cos n π cos n π = t 8 t 3 − 4 t 2 − 4 t + 1 = 0 a n s w e r − > cos 7 π , cos 7 3 π , cos 7 5 π n = 7
@Deepanshu Gupta , @Azhaghu Roopesh M check out this solution too i hope you would like it
Log in to reply
Nice solution Cody :)
Sorry but I have made some changes in your solution since I thought it was lacking somewhere , no offence !!
Just to make it look good , I did so . I believe you would want to copy the Latex off some portions and modify your solution .
∠ ( A 1 A 2 A 3 ) = n ( n − 2 ) π A 1 A 3 = A 2 A 4 = 2 a cos n π now , A 1 A 2 ⋅ A 3 A 4 + A 2 A 3 ⋅ A 1 A 4 = A 1 A 3 ⋅ A 2 A 4 a 2 + A 2 A 3 ⋅ A 1 A 4 = ( 2 a cos n π ) 2 A 1 A 4 = a ( 4 cos 2 n π − 1 ) now , A 1 A 2 1 = A 1 A 3 1 + A 1 A 4 1 2 cos n π [ 4 cos 2 n π − 1 ] = 4 cos 2 n π − 1 + 2 cos n π cos n π = t 8 t 3 − 4 t 2 − 4 t + 1 = 0 answer ⇒ cos 7 π , cos 7 3 π , cos 7 5 π n = 7
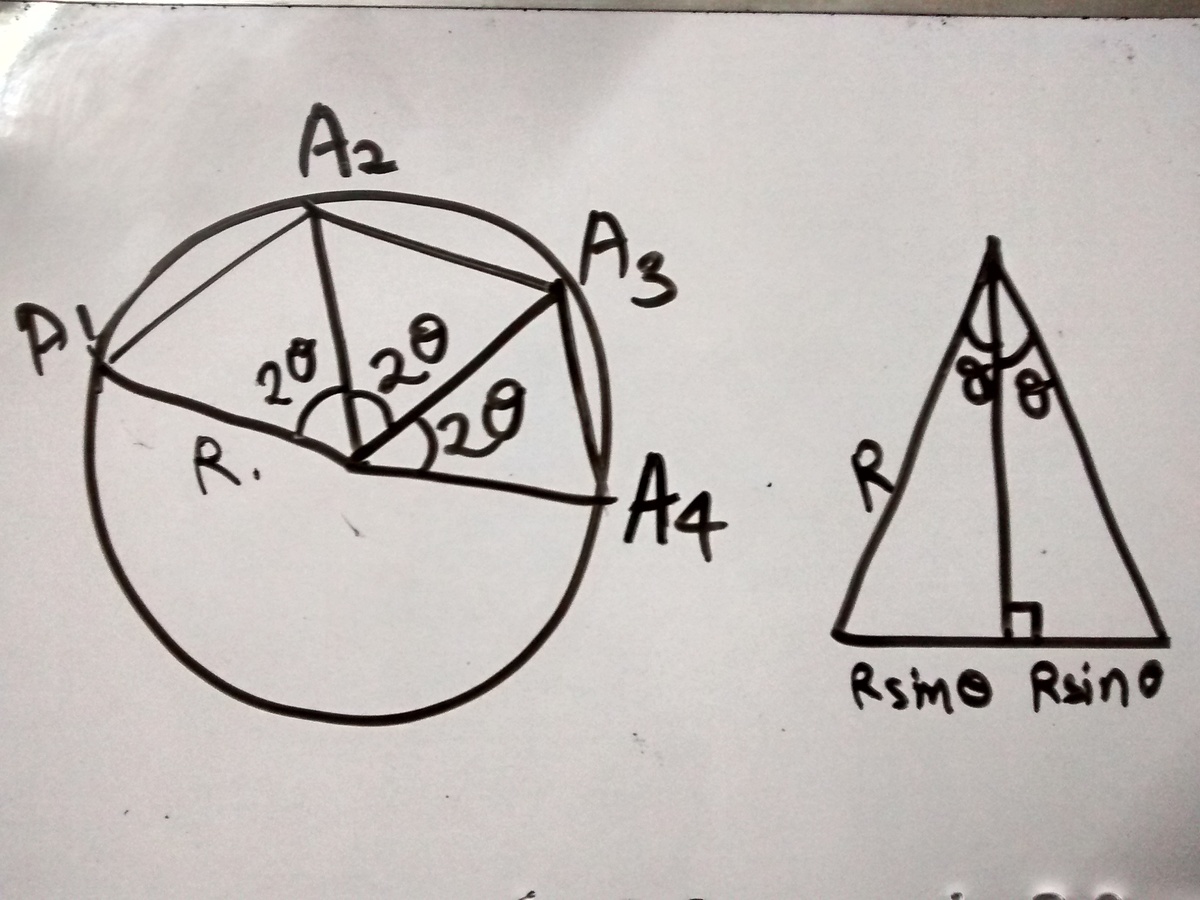
We construct a circumcircle. Thus, 2 n θ = 2 π . And θ = n π .
A 1 A 2 = 2 R sin θ , A 1 A 3 = 2 R sin 2 θ , A 1 A 4 = 2 R sin 3 θ .
sin θ 1 = sin 2 θ 1 + sin 3 θ 1
sin θ 1 − sin 3 θ 1 = sin 2 θ 1
sin θ sin 3 θ sin 3 θ − sin θ = sin 2 θ 1
sin θ sin 3 θ 2 cos 2 θ sin θ = sin 2 θ 1
2 cos 2 θ sin 2 θ = sin 3 θ
sin 4 θ = sin 3 θ
4 θ = π − 3 θ
θ = 7 π
n = 7