Which Triangle is greater in Area?
![\[\Large{\text{Which Triangle is greater in Area?}}\]](../../brioche/uploads/FAs7a8H5Xl-untitled001.jpeg?width=1200) Which Triangle is greater in Area?
Which Triangle is greater in Area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Used the same theorem. Thank you for teaching me about it.
Log in to reply
Sure, welcome, and thank you for trying my problem. Hope you liked it :)
Using negative space theorem gave a 9.5 vs 9 unit area
Log in to reply
Those numbers are far too large. Triangle A is contained in a 4x2 rectangle. See Michael's solution.
@Drago . , I got 8-5=6-3 using negative space
Hi Mahdi Raza. Seems like you too are in 10th grade like me. How have been preparing for board exams? And how do you balance your preparation for board exams with competitive exams like NTSE, PRMO,RMO etc. Please let me know. Don’t look at my account name as I am using my father’s name.My name is Chandraprakash. I am also a fellow 10 th grader(in Tamilnadu,India)
Log in to reply
Hi Chandraprakash. Yes, I am in 10th grade but in the IB board (different from CBSE) where we have to do a year-long project and write a full-fledged report, instead of giving boards. The final marks come late after our projects and reports are checked externally outside India. I don't have boards exam thus, but instead, school assessments of each subject on which we get the year-end report cards with a heavy weightage of our single year-long projects. These projects are independently done by students and no major help is used from teachers.
So for me, I don't have board exams. Coming to competitive exams, these are actually very difficult and I believe one has to study themselves with determination to crack those olympiads. I have a profound interest in Mathematics, thus I learn more and more of that. And along with a good chunk of practice, I developed a sufficient amount of prepartion for olympiads. Hope that helps.. feel free if you have any questions to ask!
Thanks! This is very interesting. I will upvote your solution :D
Log in to reply
Thank you Páll
Log in to reply
Just a question: Which is your first name? My first name is Márton :)
Log in to reply
@A Former Brilliant Member – Ok Márton, but why does it read Páll Márton then?
Log in to reply
@Mahdi Raza – Because in our country in the correct order the first name is the second. And we don't say that this is my first name or last name. If i translate that: first n.=cross name; last n.=family name. Or maybe I entered my name incorrectly.
Same Solution - fine classic theorem.
I used coordinate geometry. I regarded the lowest leftmost point as the origin, but I got it wrong...
Log in to reply
Co-ordinate may get complex really fast... Better luck next time!
I used the same theorem. I liked your problem a lot.
That is a nice solution!
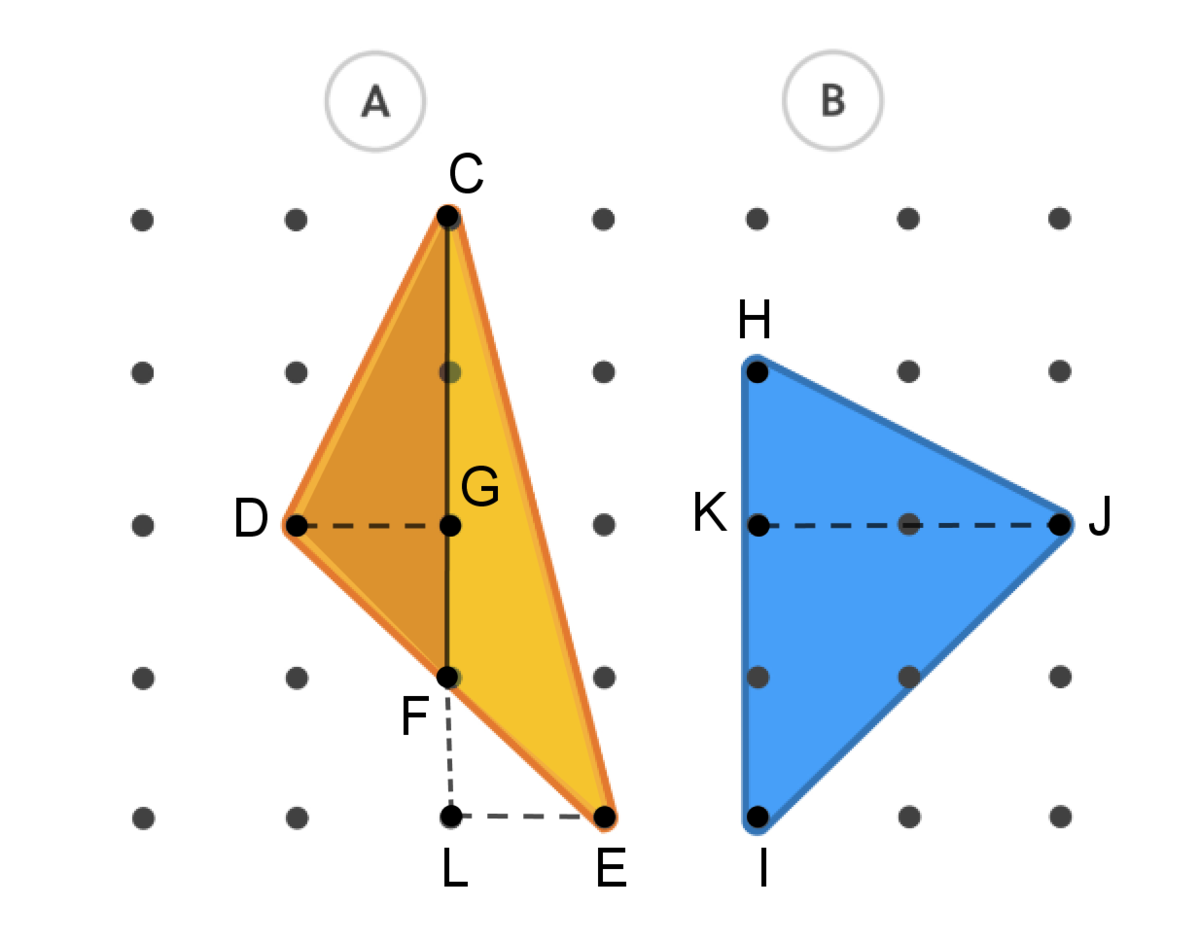
Area of △ A = Area of △ C D F + Area of △ C F E = 2 1 C F ⋅ D G + 2 1 C F ⋅ E L = 2 1 × 3 × 1 + 2 1 × 3 × 1 = 3
Area of △ B = 2 1 H I ⋅ J K = 2 1 × 3 × 2 = 3
Hence, Area of △ A = Area of △ B .
Nice dissection, same as Jerome's solution from today's problem

We can cut the top half of the orange triangle A into two smaller triangles a and b . Flip a over and place it on top of the bottom half of the orange triangle. Place b by the side of the bottom half of the orange triangle. We get a reflection of the blue triangle B . Therefore A = B in area.
Nicely done! I like it!
i liked your method
The blue (B) triangle has a base length 3 (left side) and height 2 (from right vertex to base). Triangle area = 2 b ∗ h = 2 2 ∗ 3 = 3. The gold (A) triangle area can be found by subtraction. Look at the rectangle starting at the left vertex of the triangle and 4 units tall and 2 units wide ending at the lower right vertex. that rectangle consists of 4 areas - the gold triangle and 3 right triangular spaces surrounding it. The rectangle is area = 8. The upper left space is a triangle with base = 1 height = 2, area = 1. The upper right space is a triangle with base = 1 height = 4, area = 2. The lower left space is a triangle with base = 2 height = 2, area = 2. So by subtraction, the gold (A) triangle's area = 8 - 1 -2 - 2 = 3. The triangles have the same area, 3. The gold (A) triangle area can also be found using Pick's Theorem. Arrea = 2 + 2 4 - 1 = 3.
2 1 ∥ ∥ ∥ ∥ ∥ ∥ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ∥ ∥ ∥ ∥ ∥ ∥ = A r e a ∴ ∵ ∵ ∵ ∵ 2 1 ∥ ∥ ∥ ∥ ∥ ∥ 0 2 1 1 4 1 2 0 1 ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ 2 0 1 4 1 1 0 2 1 ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ 2 0 0 4 1 1 0 2 − 1 ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ ∥ 2 0 0 4 1 0 0 2 − 3 ∥ ∥ ∥ ∥ ∥ ∥ 2 × 1 × 3 = 2 1 ∥ ∥ ∥ ∥ ∥ ∥ 0 0 1 0 3 1 2 2 1 ∥ ∥ ∥ ∥ ∥ ∥ = ∥ ∥ ∥ ∥ ∥ ∥ 1 0 0 1 3 0 1 2 2 ∥ ∥ ∥ ∥ ∥ ∥ = 1 × 3 × 2 = 6 = 6
Or a simple version:
A r e a = 2 1 ( x 2 y 3 − x 3 y 2 )
If the third( x 1 ; y 1 )point's coordinates are ( 0 ; 0 ) .
Pick's Theorem states that -- Area = Interior Points(I) + Boundary Points(B)/2 - 1
Using Pick's Theorem we get area as
For Triangle A -- I = 2, B = 4 Area = 2 + 4/2 - 1 = 2+2-1 = 3
For Triangle B -- I = 1, B = 6 Area = 1 + 6/2 - 1 = 1+3-1 = 3
Area of Triangle A = Area of Triangle B
Please consider upvoting, I went through the trouble of learning Pick's theorem from 4 different sites and then some books. Peace!!
Log in to reply
Keep learning. Upvoted!
Dimensions of A : Base = 2 2 , Height = 1 . 5 2 ⇒ Area = 3
Dimensions of B : Base = 2 , Height = 3 ⇒ Area = 3
Therefore A A = A B
Dunno aby theorems, dunno how to put the pure logic and simple maths into these fancy formulas. Got to the correct answer by just ADDING UP/SUBSTRACTING THE HALVES AND QUARTERS of grid point squares and rectangles. I wish I could do it the ‘academic way’ though
The both have same base that is 3 and altitude of first triangle is 2 and altitude of the orange triangle is sum of two altitudes both equal to 1 Hence both blue and orange triangles have same area.
Solution: Pick's theorem
For Triangle A: I = 2 , B = 4 ⟹ Area = 2 + 2 4 − 1 = 3
For Triangle B: I = 1 , B = 6 ⟹ Area = 1 + 2 6 − 1 = 3
A = B