Whiplash!
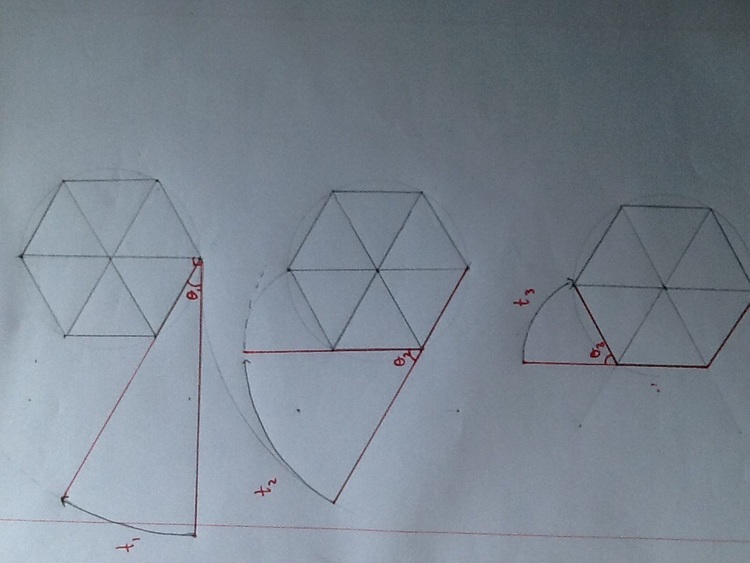 Consider a rope attached to one vertex of a regular hexagon, and originally resting at right angles with the symmetry line through that vertex. The rope moves towards the edge with a certain angular velocity. Once it comes in contact with the first edge, the rope bends around the first edge, and moves with the same linear velocity towards the second edge. Once it reaches the second edge, it curves around the edge and reaches the third side. Let the rope be
3
times the side length of the hexagon.
Consider a rope attached to one vertex of a regular hexagon, and originally resting at right angles with the symmetry line through that vertex. The rope moves towards the edge with a certain angular velocity. Once it comes in contact with the first edge, the rope bends around the first edge, and moves with the same linear velocity towards the second edge. Once it reaches the second edge, it curves around the edge and reaches the third side. Let the rope be
3
times the side length of the hexagon.
Let the time taken to reach the first side be t 1 . Let the time to go from the first edge to the second edge be t 2 . Let the time to reach the third edge after reaching the second edge be t 3 . Let the total time of motion of the rope be T .
Find ( t 1 ) ( t 3 ) ( t 2 ) ( T )
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I have an alternative way of thinking about it.
I know that ω = 2 π f , ω = T 2 π , T = ω 2 π
I also know that v = ω r , ω = r v
Rearranging I get the following:
For T 1 = r v 2 π , T 1 = v 2 π r .
As the motion progresses:
T 2 = v 2 π ⋅ 3 2 r , T 3 = v 2 π ⋅ 3 1 r ,
Here 'T' indicated the time period for a full circular path. However for T(1) only 1/12 of the period is completed and for T(2) and T(3) only 1/6 are completed. Hence
T 1 = 6 v π r , T 2 = 9 v 2 π r , T 3 = 9 v π r
T = 9 v 1 . 5 π r + 9 v 2 π r + 9 v π r = 1 8 v 9 π r = 2 v π r
Following rearrangement into the form of the answer, and because we know that 'v' is constant and clearly the length of 'r' decreases by a third for each edge 'completed':
( T 1 ) ( T 3 ) ( T 2 ) ( T ) = 6 v π r ⋅ 9 v π r 9 v 2 π r ⋅ 2 v π r = 5 4 v 2 π 2 r 2 1 8 v 2 2 π 2 r 2 = 1 8 π 2 r 2 v 2 1 0 8 π 2 r 2 v 2 = 6
In this case the solution is once again 6. :)
Only one correction: the statement "The linear velocity '' of the free end of the rope will be the same throughout since no force is acting on it in that direction" doesn't seem right to me as this is not a dynamics problem. Linear velocity remains same because it is given so, not because of absense of some force. Nice solution otherwise. :)
Log in to reply
point noted! changes made! :)
Log in to reply
u shud hv mentioned it is the linear velocity of free end
Log in to reply
@Mayank Shrivastava – Over rated problem!!!!!!!
Just use conservation of angular momentum
W1(3r)^2 = W2(2r)^2=W3(r)^2
W=(theta/time)
9w1=4w2=w3. And now since theta is the same
9t3=t1 t2=4t3 T=14t3
now 56/9=6.2 or6
Suppose the rope has initial angular velocity ' ω 1 '. After bending at 1st side, it becomes ' ω 2 ' and bending at 2nd side, it becomes ' ω 3 '
Let side of hexagon be ' a '. Therefore length of rope = 3 a
Now, the initial angle between rope and first face of hexagon is 6 π . When rope completely covers one edge, it makes an angle of 3 π with next edge. ∴ ω 1 = t 1 6 π ω 2 = t 2 3 π ω 3 = t 3 3 π
The linear velocity ' v ' of the free end of the rope will be the same throughout as it is given so in the problem statement.
Now, v = 3 a ∗ ω 1 ∴ t 1 = 2 v a π v = 2 a ∗ ω 2 ∴ t 2 = 3 v 2 a π v = a ∗ ω 3 ∴ t 3 = 3 v a π ∴ T = t 1 + t 2 + t 3 = 2 v 3 a π ∴ ( t 1 ) ( t 3 ) ( t 2 ) ( T ) = ( 2 v a π ) ( 3 v a π ) ( 3 v 2 a π ) ( 2 v 3 a π ) = 6