Equally Divided 10 Points

Probability Level 3

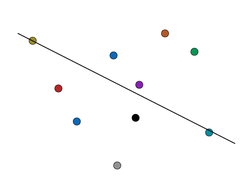Consider all set of ten points which lie in a plane and no three of them are collinear.

There are at least $x$ lines which pass through exactly two of these points, and divide the plane into 2 regions which each contain four of the remaining points.

What is the largest possible value of $x$ ?

The answer is 5.

3 solutions

Lavneesh Nyol
Oct 20, 2014

Take 10 random points in a plane with no 3 of them collinear. Choose any 1 point and start connecting it with remaining of the points.

There will only be one other point which when connected with this point divides the remaining 8 points in half (4 on each side).

For each point there is only one line which divides the remaining points in half. Hence there should be 10 lines. But, we have counted each line twice, as there will only be one line for two points.

Hence the answer is 10/2 = $\boxed{5}$

that's brilliant

Mehul Chaturvedi - 6 years, 7 months ago

Here's another: Another Another

Guiseppi Butel - 6 years, 7 months ago

How did you placed the image here (there's no option there)

Mehul Chaturvedi - 6 years, 7 months ago

@Mehul Chaturvedi I've updated the question given Guiseppi's comment. Can you review it for accuracy?

Calvin Lin Staff - 6 years, 7 months ago

@Mehul Chaturvedi As mentioned, your solution is wrong because the claim of

There will only be one other point which when connected with this point divides the remaining 8 points in half (4 on each side).

is not true.

It is true if the convex hull of the 10 points is the 10 points.

For a simple counter-example, take the vertices of a regular 9-gon, along with the center. Then, any vertex connected to the center gives us a line which splits the points into 2. Thus, there are (at least) 9 lines. You can easily see how this violates the claim of "there will only be one other point".

Calvin Lin Staff - 6 years, 7 months ago

Thanks to correct me Really thank u sir...

Mehul Chaturvedi - 6 years, 7 months ago

What about this? I count 7 lines. Dividing A Plane

Guiseppi Butel - 6 years, 7 months ago

I did consider the Green to Purple and Purple to Blue but they are very close, too close for comfort. I think there has to be at least 5.

Venture HI - 6 years, 7 months ago

Thanks! The issue with the solution is that "There will only be one other point which when connected with this point divides the remaining 8 points in half (4 on each side)" need not be true. It is true for points on the convex hull, but not necessarily true for points in the interior (like the purple point).

I agree that changing the question to ask for the greatest lower bound would be better.

I think this will make for an interesting discussion, and moved it to Dividing Line

Calvin Lin Staff - 6 years, 7 months ago

Toan Pham Quang
Nov 2, 2014

I disagrees with the answer 5. I think the answer is 4. For example, a line passes through 3 points, divides the plan into 2 regions which one contain 3 points and the other contain 4 points. In this case, I'm only get at least 4 lines which satisfy the condition.

Sorry about that, I have updated it to say "no three are collinear" instead.

In future, if you spot any errors with a problem, you can “report” it by selecting the “dot dot dot” menu in the lower right corner. You will get a more timely response that way.

Calvin Lin Staff - 6 years, 5 months ago

Dominick Hing
Oct 24, 2014

It's easier to imagine if we suppose that these 10 points are arranged in a circle. Then we can tell that for each point there is 1 other that is [almost] directly across that divides the remaining 8 points into 2 sets of 4.

There are 5 such lines that divide the rest into equal groups since for each point there is only one other point to which you can connect with a line and divide into 2 sets of four. We divide 10 by 2 since we don't want to count each line twice.

The answer is 5

Note: It is not necessary that the 10 points are arranged in a circle, or that we can manipulate it such that the 10 points are arranged in a circle.

Calvin Lin Staff - 6 years, 7 months ago

True, but doing it that way made it easier for me to see.

Dominick Hing - 6 years, 7 months ago

That is a good way to get an initial sense of the problem.

However, note that it doesn't represent all possible scenario. The problem was initially wrongly stated, as it did not cover all the possible cases, but only those that are similar to what you described.

Look at how the question changed, and think about how your solution should be updated.

Calvin Lin Staff - 6 years, 7 months ago

@Calvin Lin – Sir @Calvin Lin please remove the image of points given ion question it has became too easy, by just counting it

Mehul Chaturvedi - 6 years, 7 months ago

@Mehul Chaturvedi – I disagree. As Guiseppi pointed out, the image has 7 dividing lines, while the answer is 5.

Remember that this is the image which disproved the original version of your problem.

Calvin Lin Staff - 6 years, 7 months ago

@Calvin Lin – Would u please change the answer of it/Correct it

Mehul Chaturvedi - 6 years, 7 months ago

@Mehul Chaturvedi – The answer is 5. If one uses the image, it gives 7, which is (intentionally?) wrong.

On the other hand, as currently stated, there's this phrase "three of them are collinear" instead of "no three of them are collinear", which bumps the answer further down to 4...

Ivan Koswara - 6 years, 6 months ago

Equally Divided 10 Points

The answer is 5.

3 solutions

0 pending reports