Who likes to cut it that way?

Assume the pizza has radius $1$ .

We can find that $4 * \angle BAO = \angle BOC$ from inscribed angles. The area of the isosceles triangles $\triangle ABO$ and $\triangle ACO$ are each $\sin{x}\cos{x}$ which can be found by dividing them into two smaller right triangles with hypotenuse $1$ (see below). Using the sector area formula, the area of sector $BCO$ is $\frac{1}{2}4x*1^2=2x$ . Therefore, $2\sin{x}\cos{x}+2x=\frac{\pi}{3}$ . Solving this gets $x \approx 0.268133$ , so $\angle BOC = 4x \approx 1.072534$ . We find that $\angle BOA = \angle COA \approx 2.605326 \approx \boxed{143\%}$ larger than $\angle BOC$ , and the same perecentage applies to the crust of each slice.

Here, $DO = \sin{x}$ and $AB = 2\cos{x}$ , so the area is $\frac{1}{2}\sin{x}*2\cos{x}=\sin{x}\cos{x}$ .

We can break up the middle piece as follows, where $AC$ and $AD$ are the two cuts, $O$ is the center of the pizza circle, $AB$ is the diameter, $x$ is the measurement of $\angle BOC$ , and $r$ is the radius of the pizza circle.

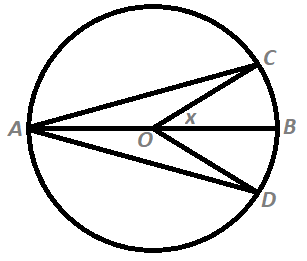
Then the area of sector $BC$ is $A_{sector} = \frac{x}{2\pi}\pi r^2 = \frac{x}{2}r^2$ , and the area of $\triangle AOB$ is $A_{\triangle} = \frac{1}{2}r^2\sin(\pi - x) = \frac{1}{2}r^2\sin(x)$ . By symmetry, the area of sector $BD$ is the same as the area of sector $BC$ and the area of $\triangle AOD$ is the same as the area of $\triangle AOB$ .

Since all of these parts must add to one third the area of the circle, we have $\frac{1}{3}\pi r^2 = 2(\frac{x}{2}r^2 + \frac{1}{2}r^2\sin(x))$ , which simplifies to $\pi = 3 \sin(x) + 3x$ . Solving numerically gives $x \approx 0.53626698$ .

Since the crust of the upper slice is $\pi - x$ , and the crust of the middle slice is $2x$ , its percent increase is $\frac{\pi - x - 2x}{2x} \cdot 100\% \approx \boxed{143}\%$ .

Calling $2\theta$ the angle of the smallest arch seen by the centre of the pizza, expressing the area of the central slice as function of $\theta$ reduces to solving numerically $\theta+\sin\theta=\frac{\pi}{3}$

I've done this iteratively

$\theta_0=\frac{\pi}{3}$

$\theta_{i+1}=\frac{\theta_i + \pi/3 - \sin\theta_i}{2}$

After 9 iterations this gives 0.536266979

The rest is straightforward, $X=\frac{\pi-3\theta}{2\theta}*100=143$

The area of the top piece is the area of a segment of a circle. This can be found by taking the area of the sector that contains it and subtracting the area of the triangle in that same sector. Let's call the central angle of this sector measured in radians x. Area of sector

1/2 x * r^2

Area of triangle

1/2 * 2 sin(x/2) * cos(x/2) * r^ 2=

1/2 sin(x) r^2

Let's say r = 1 to simplify calculations The area of this segment has to be equal to 1/3 of the total area, which is pi/3

Area of sector - Area of triangle

x - sin(x) = 2pi/3

x approximately = 2.605 The crust of this segment is x And the crust of the large segment is 2pi - 2x Solving for both of these, finding the percent increase, and rounding to the nearest integer gives

143