Who Needs a Calculator

Rewrite the equation as

$\sec^{2}(\theta) - 1 = \sec(\theta) \Longrightarrow \sec^{2}(\theta) - \sec(\theta) - 1 = 0$

$\Longrightarrow \sec(\theta) = \dfrac{1 \pm \sqrt{5}}{2}$ .

Now since we are looking for the smallest positive value of $\theta$ we take the positive root for $\sec(\theta)$ and then calculate the corresponding value for $\tan(\theta)$ :

$\tan(\theta) = \sqrt{\sec^{2}(\theta) - 1} = \sqrt{\frac{3 + \sqrt{5}}{2} - 1} = \sqrt{\frac{1 + \sqrt{5}}{2}}$

$\Longrightarrow \theta = \tan^{-1}(\sqrt{\frac{1 + \sqrt{5}}{2}})$ .

Thus $a + b + c = 1 + 5 + 2 = \boxed{8}$ .

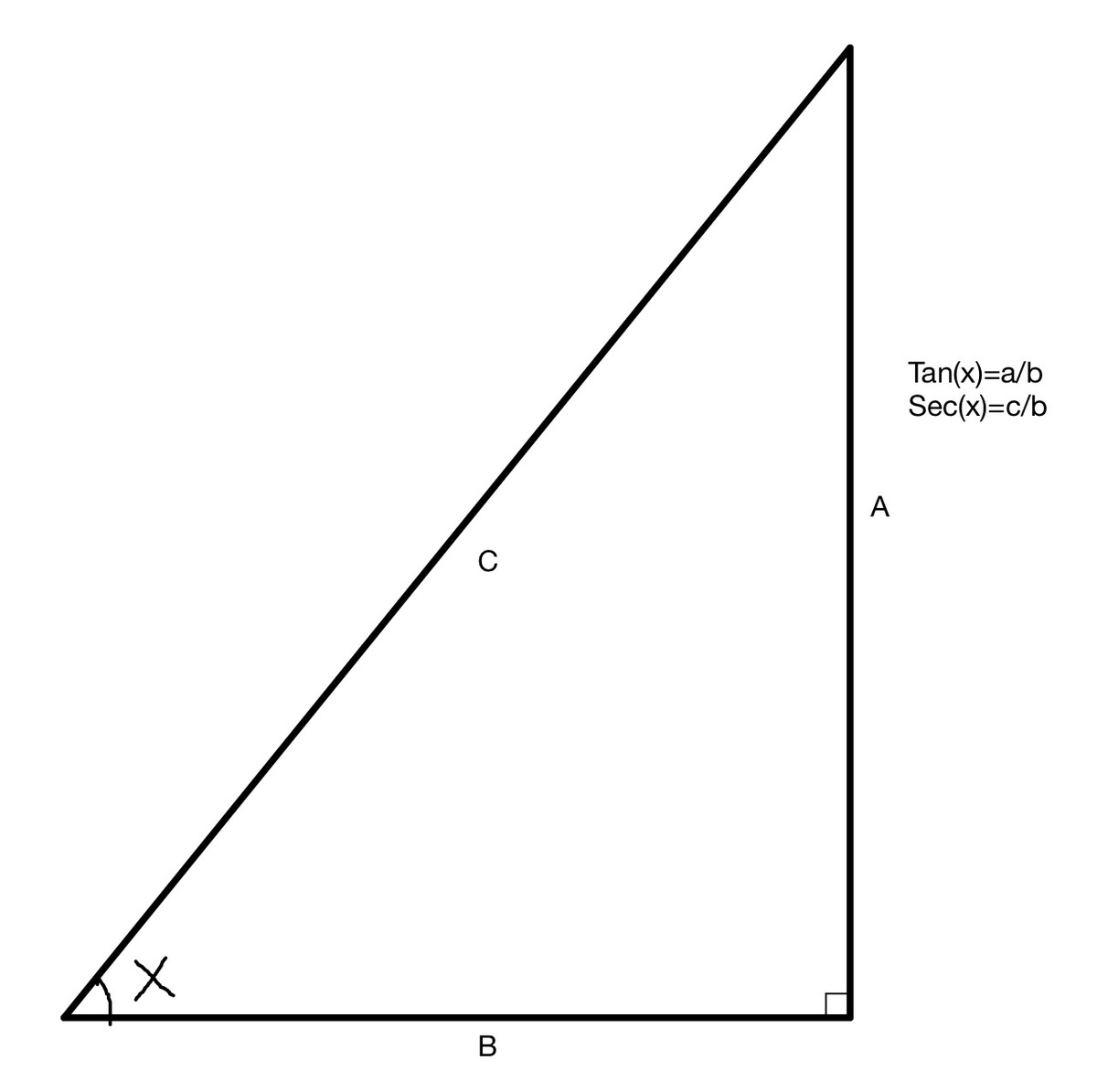
Begin with the triangle depicted above. Btw, I replace $\theta$ with $x$ cuz I'm too lazy to type \theta lol.

We have $\tan(x)=\frac{a}{b}$ and $\sec (x)=\frac{c}{b}$

$\therefore \tan^2(x)=\sec(x)\Rightarrow \frac{a^2}{b^2}=\frac{c}{b}$

$c=\frac{a^2}{b}$

Now, Pythagorean theorem yields

$c^2=a^2+b^2\Rightarrow \dfrac{a^4}{b^2}=a^2+b^2$

$a^4-a^2b^2-b^4=0$

Since we are looking for real positive roots, we ignore both $\pm$ and make them positive,

$a=\sqrt{\dfrac{b^2+\sqrt{b^4+4b^4}}{2}}$

$a=b\cdot \sqrt{\dfrac{1+\sqrt{5}}{2}}$

Therefore, since $\tan(x)=\frac{a}{b}$

$\tan(x)=\dfrac{1+\sqrt{5}}{2}$

$x=\boxed{\tan^{-1}\left(\dfrac{1+\sqrt{5}}{2}\right)}$

Therefore, $a+b+c=1+5+2=8$

Using the Pythagorean identity for tangent-secant: ${tan}^{2} \theta = \sqrt{{tan}^{2} \theta+1}$

Let $u={tan}^{2} \theta$ ; hence, $u= \sqrt{u+1}$ . Squaring both sides yields the golden ratio quadratic ${u}^{2} -u-1=0$ . Thus $\theta = {tan}^{-1} \left(\frac{1+\sqrt{5}}{2} \right).$