Who takes two language subjects?
Out of a group of students, 60% are taking mathematics, 65% French, and 75% German, but none are taking all 3 subjects.
Is there a student who is taking neither French nor German?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Very straight forward I over-thunk the problem.
I started reading this half expecting a troll. Simple solutions are so elegant
Log in to reply
That's cause my teacher used to penalize me when my answer is not the shortest. So i am always trying to make my solutions as simple as possible :)
None of them taking "3" actually
Where is it specified that there are only these 3 subjects? What if every french student is doing german, then 75% are doing French or German. Maybe a few of the rest are doing maths.
PS that would be me
Log in to reply
As far as I can see, whether any other subjects exist makes no difference to the solution, since we care only about the numbers of people doing these particular subjects (individually or in combination). Or am I missing something?
can you please explain your solution more clearly. Thanks in advance
Log in to reply
The number of subjects taken is twice the number of students (200%). Then there are two cases: 1) N are taking 3 subjects, N are taking 1 subject, and the rest are taking two subjects. 2) All of them are taking 2 subjects. As none are taking all 3 subjects we must be in the second case.
Log in to reply
Why is this not your solution??? You current solution does not explain it at all.
Log in to reply
@Chris Arsenault – Cause I prefer short solutions. And I want you to work a little bit to understand it :)
So if 200% of the classes are being taken, and no one is taking 3 then no one can take one, so everyone is taking 2 classes
Nice solution. To help those who don't get it you could insert a line stating that 'On average each student takes two subjects. Then since none are taking three... etc
What I need to learn to solve like you did. Good Vibes!
That's how I solved it too!
If 50% of the students are taking only 1 class, then your solution is flawed. The information provided does not say all students were taking 2 classes you made an assumption they were. The question is poorly framed.
Log in to reply
How is it possible, under the constrains of the problem, for 50% of the students to be taking only one class?
Great solution!
It is a solution, definitely. Good job!
I don't agree. What if 25% of the students are taking only math? There is no constraints about that in the given info.
Log in to reply
How is this possible under the constraints of the problem? Please give a full set of percentages for the various combinations that satisfies both "25% of the students are taking only math" and the statements in the problem.
What an odd school where all of the students take exactly 2 classes. None of them take only one?
Consider the case when there are 20 students. Then 12 take math, 13 take French, and 15 take German. These numbers add up to 40, which is twice the actual number of students.
Let's imagine a student who takes French and math. This student counts towards the math and the French total, so the student is counted twice. Since the total is twice the number of students, that means that every student is counted twice, so every student takes two subjects. No student can be counted three times since no students take all three subjects.
This means there isn't a student who doesn't take French or German.
If there were a student which takes all three, there would be a student who takes just one subject, possibly math. Therefore, it's important to mention that none of the students take all three.
Log in to reply
Regardless...if there are 6000 students in this school, the question is supposing by saying out of a group only a portion are televant to the problem being asked about.
While that's all well and good, it doesn't follow logically because the question is framed poorly.
"Out of a group of students, 60% are taking mathematics, 65% French, and 75% German, but none are taking all 3 subjects.
Is there a student who is taking neither French nor German?"
The setup to the question specifies "Out of a group of students", implying a subset of all students. While the question "is there a student who is taking neither French nor German" does not specify that same subset. It does not say "Is there a student in that group" - it says, "is there a student..." The "correct" answer to the question hinges on ignoring the information specified in the question, and only approaching it from a face-first, obvious angle. How is this helpful or relevant?
Log in to reply
I agree with this. The phrasing of the question promotes closed thinking. Other questions have an "Impossible to know" answer choice so this seems to be a contradiction to me.
I agree the question was poorly framed.
We can imagine a easiest way like we know there are 60% students take Mathematics, the best situation for Mathematics' student is the rest of students (40%) take both French and German.
Then there are still gonna be 25% for French and 35% for German, since none are taking all 3 subjects, there will only be French-Mathematics and German-Mathematics students = 25% + 35% = 60%
Thus, there aren't going to be a student who only take Mathematics = neither French nor German.
The answer is No

The only grouping possible for 60% of the students taking Mathematics, 65% taking French, 75% taking German and none taking all three subjects is as shown the figure above. That is: 35% taking Mathematics and German + 25% taking Mathematics and French + 40% taking Frech and German = 100%. Therefore, there is no student taking neither French nor German.
This is how worked it out using a circular scale, same result but my drawing was rubbish.
Here's a solution using a Venn-diagram:
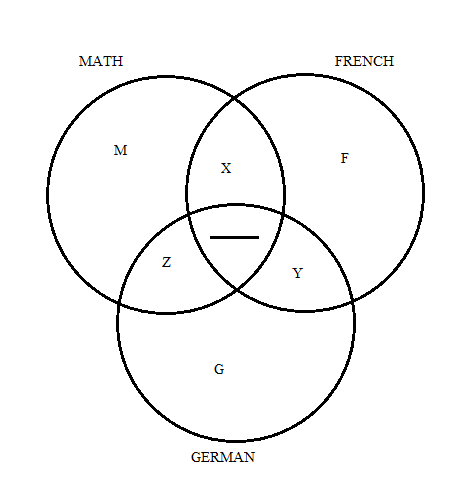 We know that:
M
+
X
+
Z
=
6
0
,
F
+
X
+
Y
=
6
5
,
G
+
Y
+
Z
=
7
5
,
Which gives us :
M
+
F
+
G
+
2
X
+
2
Y
+
2
Z
=
2
0
0
.
We know that:
M
+
X
+
Z
=
6
0
,
F
+
X
+
Y
=
6
5
,
G
+
Y
+
Z
=
7
5
,
Which gives us :
M
+
F
+
G
+
2
X
+
2
Y
+
2
Z
=
2
0
0
.
We also know that M + F + G + X + Y + Z = 1 0 0 so
1 0 0 + X + Y + Z = 2 0 0
X + Y + Z = 1 0 0
That means M + F + G = 0
so M = 0
Very good. Venn diagrams are the classic way to solve problems like this. But wouldn't your statement M = 0 also imply that F & G are also equal to zero in view of the equation M + F + G = 0 ?
Log in to reply
Exactly. Thats because there is no student who takes one subject alone.
I like this - but 1 question that’s bothering me. How do you know that M+F+G+X+Y+Z =100? The question never stated the total number of students is 100.
Log in to reply
Good question! You don't actually know, I just assumed because it's easier to think about percentages with 100 students. Assuming that there are 100 students in total doesn't influence the percentages or the solution so you can do it freely.
(You can also think about the 100 in the equation as 100%, not 100 students. You're right, I should've made this clear, thank for pointing this out. :D )
I looked at each course registered for by a student and created a table based on the problem assuming 100 students.
German 75
French 65
Math 60
Total 200
Students 100
Avg Courses 2
Since no student can register for more than 2 courses they can only register for 0 or 1 or 2.
Since the average number of courses registered for by the 100 students is 2, none can be anything other than 2, since any that take 0 or 1 would lower the average to less than 2.
 Changing who takes French or German from this would result in students taking all three subjects.
Changing who takes French or German from this would result in students taking all three subjects.
Man it's so easy "group of students" if you don't study you are not a student. Then the answer is no
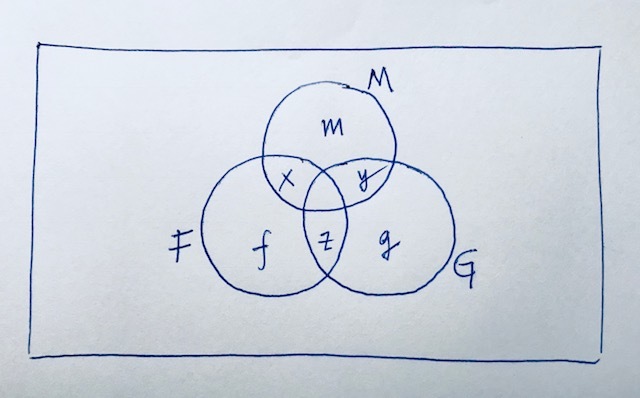
{ f + m + g + 2 ( x + y + z ) f + m + g + x + y + z = 2 0 0 % = 1 0 0 %
Subtracting the second equation from first gives x + y + z = 1 0 0 % , which means that m = 0 . Therefore, no student is taking math only.
Let there be 100 students in total . So 60 are take maths ,65 take French and 75 take German. Let there be one studen who is neither taking French nor German thus he has selected only maths. As there are 60 and 65 students in maths and French, at least 25 students have opted for both (60 +65 -100 =25) . So 75 students who opted for German must be the 75 students which are left (because there is no student who selected all three subjects) So there is no student who selected only maths.
improve more
If we create a Venn Diagram, and call the percentage of students that takes both Math and German a , the percentage of students that take both Math and French b and the percentage of students that take both German and French c , the percentage of students taking Math only will be 6 0 − a − b , the percentage of students taking German only will be 7 5 − a − c and the percentage of students taking French only will be 6 5 − b − c .
When we sum up all the values in the Venn diagram we end up with the total of the students, in this case it is 100 %.
6 0 − a − b + 7 5 − a − c + 6 5 − b − c = 2 0 0 − a − b − c = 1 0 0
Hence, a + b + c = 1 0 0 .
If there are no students taking both German and French we have c = 0 and a + b = 1 0 0 . But if so, the percentage of students taking only Math will be 6 0 − 1 0 0 = − 4 0 which is impossible!
Hence, we can conclude that must be some students that take both German and french and this number must be greater than 40% of the total.
Let's look at it another way, by inverting the percentages. We have 40% of the students not doing maths, and 35% not doing French. This means at least 25% of the students are doing both maths and French. By the same logic, at least 35% are doing both maths and German, and at least 40% doing both French and German. Since nobody is taking all three subjects, these three categories are disjoint. Hence, since the percentages add up to 100%, this means at least 100% of the students are taking two of the mentioned subjects. Since it can't be more than 100%, it must be exactly 100%. So every student is taking two of the three mentioned subjects. Ergo, nobody is taking neither French nor German. QED
To account for all students in the allowed combinations of two subjects only, some must take Maths and French (60% + 65% > 100%, so clearly some students take both), and some must take Maths and German (60% + 75% > 100%, so same story, some must take both). The case of students who take both French and German does not need to be considered in the context of the question. We can see that to account for all students, there is no possible solution that excludes both French and German.
The simplest solution to me seems to simply add people who take French and who take German, i.e. 65% + 75% = 140%. As this number is higher than 100%, there must be students who take both French and German.
Yes, but what if the values were 10% math, 60% french and 60% german? You'd be right in saying that some (at least 20%) must be taking both french and german, but the problem asked whether there can be students that AREN'T taking either...
Log in to reply
But that's my point. If there are students who MUST take both, there cannot be students who take neither.
65% are taking French, that leaves us with 35% who are not, In the best case all of them are taking German and out of the entire 75%, 40% are taking both. None of them can take mathematics so all the other 60% are taking Math. Let's assume not everyone who doesn't take French takes German than they must take all the 3 courses. In contradiction to the data.
Given 75% learn German so only 25% are not German students. Since 65% learn French, it is obvious that considerable number of students learn both.
Yes, at least 40% learn both, but the problem is asking about students that learn NEITHER...
Since French and German each exceed 50%, there must be students in each subject Ed Gray.
We have 65% + 75% + 60% = 200%. Since none is taking three subjects then all of them are taking two subjects. Then the answer is no.