Why are you in a hurry?
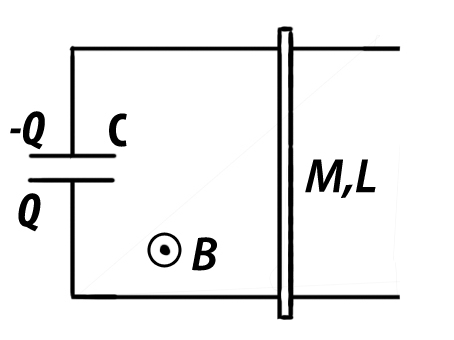 An arrangement of smooth pair of
long
conducting rails which are
non resisting
are joined to a
charged
capacitor. The rails are connected by a rod of mass
M
, length
L
, and Resistance
R
. A vertical Magnetic Field
B
is established in the region. The rod starts moving due to the influence of the Magnetic Field.
An arrangement of smooth pair of
long
conducting rails which are
non resisting
are joined to a
charged
capacitor. The rails are connected by a rod of mass
M
, length
L
, and Resistance
R
. A vertical Magnetic Field
B
is established in the region. The rod starts moving due to the influence of the Magnetic Field.
What should be the mass of the rod M (in mg) so that its Kinetic Energy in steady state is maximum ?
Details and Assumptions:
∙
L
=
1
m
∙
B
=
2
T
∙
C
=
1
μ
F
∙
R
=
1
ohm
∙
The Rod is initially at
rest
∙
The Magnetic Field is
constant
and
uniform
in nature
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I don't understand the last part, Why I got the derivative respect to M like this ( B 2 C L 2 + M ) 3 B 2 C L 2 − M but the rest is same M = B 2 L 2 C ?
Let, at a general time
t
,
Current through the rod
=
i
Then,
we know that the
Force
on the Rod
=
B
i
L
Hence,
B
i
L
=
M
a
, where
a
is the acceleration of the Rod
⇒
B
L
d
t
d
q
=
M
d
t
d
v
⇒
B
L
∫
Q
q
d
q
=
M
∫
0
v
d
v
⇒
B
L
(
q
−
Q
)
=
M
v
Also,
When the velocity of the Rod is
v
, the EMF induced in the rod is
B
L
v
Hence,
q
=
C
V
=
C
(
B
L
v
)
Substituting the value of
q
,
B
L
(
C
B
L
v
−
Q
)
=
M
v
⇒ v = M + C B 2 L 2 B L Q
Thus,
Kinetic Energy K
=
2
1
M
(
M
+
C
B
2
L
2
B
L
Q
)
2
Differentiating with respect to
M
,
d
M
d
K
=
0
2 1 − M + C B 2 L 2 M = 0
⇒ M = 4 × 1 0 − 6 K g = 4 m g
i = − d t d q , not d t d q , and hence, B L ( Q − q ) = M v
Log in to reply
Sorry, I forgot to put in the "-" sign.
Log in to reply
But if you were asked to find velocity as a function of time, all that followed would also have been wrong :P
Anyways, cute problem. A variation could also involve finding the heat loss.
Log in to reply
@Jatin Yadav – Thanks. I think I might post a couple more problems of this type involving capacitors, inductors etc., when I get free time...as I am working on Organic Chemistry notes and problems.
Log in to reply
@Anish Puthuraya – Wait! All that follows is still wrong :P
Log in to reply
@Jatin Yadav – Just ignore this solution...i dont know what I did. Yours is a much better solution.
Log in to reply
@Anish Puthuraya – 240 problems in 2hrs
@Anish Puthuraya – Do you yourself make these questions
In this problem , our primary aim is to find the steady state velocity. This can be done by two methods, method one is more important, as it involves more learning.
_ Method-1 : Finding v(t) _
Let us consider the given figure. Clearly the current will start flowing anticlockwise. Hence, lorentz force would act forward. Also, there will be an induced EMF due to the motion of rod. Let, at a time t , the current is i , charge at capacitor is q , and the velocity of rod is v .
Clearly, i = d t − d q (as q is decreasing.).
Also, the lorentz force is i L B , hence, the rate of change of velocity,
d t d v = M i L B = − d t d q M B L , note that i = B L M d t d v
Hence, we get : d v = − M B L d q ,
Integrate to get:
v = M B L ( Q − q ) ⇒ q = Q − B L M v
Now, we apply kirchoff's voltage law in the circuit, also considering the induced EMF, which clearly equals B v L .
B v L + i R − C q = 0
⇒ B v L + B L M R d t d v − C ( Q − B L M v ) = 0
Rearrange to get:
B L Q − ( B 2 L 2 C + M ) v d v = M R C d t
⇒ ∫ 0 v B L Q − ( B 2 L 2 C + M ) v d v = ∫ 0 t M R C d t
⇒ v ( t ) = B 2 L 2 C + M B L Q ( 1 − e − M R C B 2 L 2 C + M t )
Clearly, v in steady state would be v 0 = B 2 L 2 C + M B L Q .
Method-2 : Effortless.
Clearly, in steady state, the velocity becomes constant and hence the net force becomes 0 . Thus, i also becomes 0 . Hence, using Kirchoff's voltage law equation, we get:
q = B v 0 L C .
But we have already proved that v = M B L ( Q − q )
⇒ v 0 = M B L ( Q − B v 0 L C ) .
Solve to get v 0 = B 2 L 2 C + M B L Q
Maximising kinetic energy
Clearly, kinetic energy at steady state is K = 2 1 M v 0 2 = 2 B 2 L 2 Q 2 ( B 2 L 2 C + M ) 2 M
To maximise K , we have to maximise ( B 2 L 2 C + M ) 2 M , as other term is constant.
Rest part involves taking derivative with respect to M and putting 0 , i.e.
( M + B 2 L 2 C ) 2 M − B 2 L 2 C = 0 ⇒ M = B 2 L 2 C .
Put values to get M = 4 mg