Why don't you throw coins into wells and make wishes?
This picture does not necessarily show optimal play.
My friend and I play a game in which we take turns placing identical coins on a circular table one at a time.
- I place the first coin on the empty table.
- The coins are placed flat on the table. They cannot overlap or go over the edge of the table.
- The person who places the last coin on the table wins.
Which player can always win if they play optimally?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
My English is broken today. Sorry!
Log in to reply
There's nothing wrong with your English. I gave my solution to fit the answer "me". I'll fix it now.
Don't change anything.
Technically, answers are "I do"\"My friend does"(Whatever you want, since it is unreasonable given the premises of the game that there would be no winner.)
What if the table is smaller than one coin? Then the friend has a winning strategy...
Edit: sorry about that, I mean no one wins if the table is small. It is not true that the starting player has a winning strategy in all the cases
2nd Edit: The description of the problem changed, it is ok now, originally said "I go first" instead of "I place the first coin"
Log in to reply
I agree, this is a case that really needs to be stated in the problem. As it stands, cannot be determined is correct.
No. The friend does not win because he is not "the last one to place a coin." In order to be the last one to place a coin, one has to actually place a coin.
Log in to reply
Yes, sorry for that, but still no one wins in that case, so there is no winning strategy for the first player
The rules cannot be fulfilled in such a case, that is "I place the first coin on the empty table." cannot be followed as a rule. If the game cannot be played as described then it's not asking about the real game.
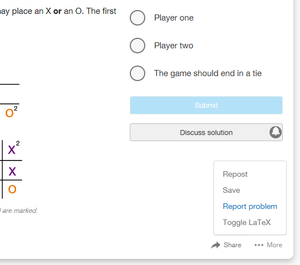
At any given point in time, starting with the orange guy, orange coins on the table should either be equal to the blue coins or 1 more than the number of blue coins. In the figure, I see 9 orange and 7 blue coins.
Log in to reply
The pictures in easy puzzles if not disclaimed below or instructed to what they are meant to mean are most often there to just give a visual cue without necessarily being accurate.
Log in to reply
I reckon the positioning of coins would play a part in deciding the final outcome, because if 2 orange coins were not placed near the circumference, the answer might as well be different
What you described is not what is pictured, so you have not determined which player has a winning strategy. I'm super confused.
It's never stated that the coin cannot be pushed when placing your coin. The blue can take the center.
The problem never states that coins cannot be pushed. Without that constraint, the problem is reduced to a circle packing problem, in which we determine if an even or odd number of circles of diameter d1 can be packed into a circle with diameter d2, and that can't be determined from the information given.
Log in to reply
It's a game-theory problem, not a sphere-packing problem.
Log in to reply
It’s intended to be a pretty straightforward game theory and spatial reasoning problem, I think, which is why it needs just that one little clarification. I’m sure it was clear to you, but it wasn’t to me and a couple others for the same reason.
Log in to reply
@Richard Peterson – Sorry, but it seems pretty obvious to me that coin-pushing is well outside the scope of the problem's framework. The language of "placing coins" does not reasonably allow a player to be moving previously placed coins.
It's OK to require the reader to make normal assumptions about the scope of a question. It's pretty much impossible to anticipate any wrinkles that some reader might want to introduce. Can the coins be placed on their edges?
Log in to reply
@Richard Desper – That’s fair. What’s obvious to one person won’t be obvious to another.
I figure that if a significant portion of the audience misunderstands a problem itself, in spite of having the prerequisite training or knowledge to solve the puzzle, then the problem may not be well specified. So does a significant portion of the audience misunderstand this problem? I don't know. What I do know is that I misunderstood it, in spite of having done well at a few discrete math courses and logic courses at school, and that another person in the comments misunderstood the problem in the same way. So that's two of us. Maybe we're the only ones.
I know I'm going to be accused of being pedantic, here, but you just outlined a strategy which results in the 1st player winning every time, but we don't know if this particular player is aware of that strategy. All we know is that he's going first. He might not even have a strategy. He might have consulted his horoscope for advice. Can it be demonstrated that the 1st player can't lose, regardless of how inept he is?
Log in to reply
Brilliant.org makes an effort to have the best wording in the Problems of the Week, and that the answer is correct and unique. But, oh well.
Log in to reply
Aaanyway...
I didn't mean to suggest there was anything wrong with your answer. What I probably should have said was something like: That's a good answer to a perfectly reasonable interpretation of a perfectly reasonable question, (and thank you, both) but if one was to be unreasonably pedantic... What follows is pure pedantry for the sake of pedantry. If that sort of thing offends you, stop reading now:
Consider a couple of scenarios:
1) Player 1 (not aware of the winning strategy) puts his coin on the table with the centre of the coin more than one coin radius from the centre of the table, but less than 2 radii. Player 2 mirrors this move and every subsequent move. Player 2 wins.
2) Player 1 is aware of the 'winning strategy'. So is player 2. Player 1 wants to go first. So does player 2. How do we decide who goes first? Does player 1 always get to choose who goes first? Then the game is rigged. Do we toss a coin? Then the winning strategy is dependent on circumstances beyond the player's control. This is not much of a strategy.
If the question was 'in order to guaranteed a win for myself, who should go first?' then your answer is perfect, but that isn't the way the question is worded. The question asks 'who has a winning strategy.' The answer assumes the first move was the result of strategy rather than luck, fate or impulse.
Like I said, though, it was a good question with a cunning solution. Cheers, both! :)
The question is whether there exists a winning strategy .
this strategy would certainly cause a win for the first player every time, but that strategy is not being employed here by player one. Also, as I noted below, there are too many orange coins on the table, of you take turns, and orange places first, there are too many orange/not enough blue.
The strategy appears to be orange cheating by placing an extra coin, and that strategy failed.
Apearently I was wrong (cannot be determined). As somebody said before me: Its just a picture nothing more (like orange extra turn). But some other pictures of other questions are crucial to solve the problem. So is there another thing about these riddles? Decide if picture is even relevant and not misleading for solve?
Log in to reply
The image has been updated and the problem has been clarified. Sorry for the confusion!
According to the picture, the blue wins the game since the number of blue coins is the number of orange coins minus 2. The orange started the game so it should always be one coin ahead of the blue. The difference 2 here means that it's now the blue's turn. Again based on the picture, the blue will be the last person to put a coin on the table since there is not enough space for a new coin in the next turn. So the blue wins! But it's not the correct answer. I'm not sure how your solution applies to this question since there are no coins at the center of the table.
I'm confused. I don't see any "orange" or "blue" coins. Are we talking about the same problem?
Log in to reply
The diagram has been updated since the problem was published. Substitute “heads” and “tails” for orange and blue.
Hello all. We had a user posting insulting comments in this thread. That user has been banned, and the offending comments have been deleted (as well as their responses). I apologize for the unpleasantness this has caused.
Log in to reply
Thank you.
Ikoz Manzukovski were creating uncomfort in me and some other people.
Thanks Andrew. It’s nice to focus on the problems and the learning. How did you discover the comments in question? Is there a reporting mechanism? I use the website, and I don’t see an option to report a user or comment.
Log in to reply
We currently do not have a mechanism to report users. The best way to reach the Brilliant staff is by using the "report" feature on the problem itself. Click on the 3 dots at the lower right side and select "report problem."
Noone can win. I'll place the last coin on the table, but it will fall from the edge. My friend will do the same, so I can do the same again. It is stated that "the person who places the last coin on the table wins". The one with most patience will.
Log in to reply
Lol I like this interpretation. Two people endlessly placing coins on the table edge. So whimsical.
Wonderful. You broke the game.
Log in to reply
My friend actually has the winning strategy, but too bad for him, I'm making the first move because of a coin flip. Buhwahahaha
The question asks "who has a winning strategy". Given the information above we have no idea whether the questioner ("I" in the question) has adopted the suggested solution (which is very clever and not something I had spotted) or not. So we can't determine who, if anyone, has a winning strategy.
Log in to reply
Yeah, I pointed that out but got nothing but opprobrium for it, so good luck. I'm glad someone agrees with me, though.
I suppose that, by "has a winning strategy", what is meant is "has available a strategy that will force a win". Whether this player actually plays by this strategy, or even knows it, is then another matter entirely.
The best way to win is to take all your opponents coins.
Please tell me if I'm looking at this wrong. If the table can optimally hold an even number of coins, Player 2 will always win. If the table can hold a maximum of an odd number of coins, Player 1 always wins. Until the game is played once, "optimally" there seems to be no way to determine what the outcome will be.
Log in to reply
The number of coins that can fit on the table depends on how the coins are placed. If you follow the method that Michael Mendrin gives, then the table will always have an odd number of coins on it when the game is over, and player 1 will always win.
Log in to reply
Slightly adjusting the diameter of the coin in relation to the diameter of the table will change the number of coins it takes IF played in a truly optimally manner. The way of playing that Michael is describing is not ALWAYS going to the optimal way. There are going to be possible permutations of the game (different combinations of the diameter of the table and of the coin being used) that will result in a gap large enough between each of the coins (if played the way Michael describes) that when added up, will result in enough room for one extra coin to be added assuming the coins are all shifted to allow the final coin to be placed. Assuming you're playing "optimally" (which in my opinion would be placing the coins in such a way that as many coins are placed as possible) then there certainly are possible permutations of the game that can be used where the person placing the second coin would win.
Log in to reply
@Don Alonzo – This is a game of placing coins. Pushing the coins is not allowed.
Log in to reply
@Andrew Hayes – Still, how can we be sure that placing a coin in the center guarantees that the number of all the coins will be odd? (I'm not saying it won't, I just don't feel that I grasp why that's the case).
Log in to reply
@Piotr Święs – Thành opens by placing a coin in the centre. Once the friend has placed a coin, Thành places a coin diametrically opposite it, so that the configuration has rotational symmetry of order 2 about the centre. Because of this symmetry, wherever the friend places a coin, Thành can place a coin diametrically opposite it, and the symmetry is maintained. So whenever Thành has just moved, if there is room for another coin anywhere on the table, there is also room for a coin in the diametrically opposite location.
@Piotr Święs – Notice that when player 1 mirrors player 2's moves, the available space is also mirrored. This ensures that the end state of the game is always similar to the situation below:
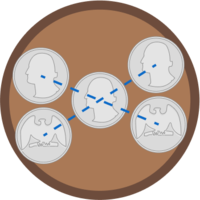
If the coins were packed optimally, then there would be room for 8 coins. However, the mirroring of the coins and available space ensures that there's only room for at most 7 coins.
Some places on the table may be blank but not enough to hold another coin
So if you place first and are the odd coin, player #2 will always be the even coin and every table size to every coin size will end as only odd numbers of coins fit, this is what it boils down to, if you place 1st you will always win because the last coin played will be odd everytime. so if only a odd number of coins fit on every table does it matter if you start in the center and mirror #2 if only an odd number of coins fit on the table?
Log in to reply
The number of coins that fit on the table depends on the way the players place the coins. The described strategy simply forces the number of coins that fit to be an odd number, however, under nonoptimal play, it could be even
Well it's very easy if you can intuitively make a reflection on a graph. Imagine the circle as a graph and divide it with x and y axis, make your first move in the center of the circle where x and y axis intersect, then whatever your opponent plays next, mark the opposite mirror of that point. For instance, if your opponent plays -1, -2 you will just have to play 1,2. You will never run out of reflections, whilst your opponent will run out of moves eventually.
The last coin placed on the table wins, the number of coins that fit on the table is undetermined. So if you place the first coin you will always be odd and if you place 2nd coin your always an even number, the final number of coins that fit on the table will determine the winner.
Log in to reply
The key is that if the first player takes the exact center, he can gauruntee that the table will only hold an odd number of coins
Log in to reply
The players would move the coins already on the table to fit theirs in. It doesn’t make any difference where the previous coins are placed - only the number of coins that fit on the table determines the winner.
Looks like orange has taken an extra turn. Orange has nine coins on the table while blue has only 7. At the end of blues turn they should have the same number of coins as orange. So somewhere orange has taken an extra turn.
So, this game, as depicted, is in violation of the rules as stated. But, that being as it is, when blue places his 8th coin as depicted, there will be no place for any additional coins. Blue wins even though Orange cheated.
Log in to reply
Thus it should be correct that blue has the winning strategy, but that answer is said to be incorrect. I don't think this question was created properly. I seem to have gotten it wrong, but the more I see in the solutions, the more I am convinced that I am correct.
It seems like this question was legit until there is this picture. Orange start first, Blue skip a turn. It seems it is blue turn now so no place for orange and blue would win according to the game rule.
one hundred percent agreed, the question is flawed. I thought I buggered it up, so I counted orange and blue a bunch of times, then placed bottlecaps down left to right to make sure, and orange has taken an extra tun.
So if the strategy was to cheat by taking an extra turn, the strategy failed.
It's just a picture. The question is about who has a winning strategy, not who will win the game in the picture.
How is going first a strategy? We cannot determine either players strategy from this question or the picture. You're inferring that he employed a winning strategy just because he went first...what if his strategy was to place as many coins around the edge of the table as possible? It's a bad question and the picture makes it worse.
Edit: Re-read the question for the 8th time and I finally get what they're trying to say. It's just worded so vaguely.
yup this is flawed because of the picture
Log in to reply
There is also not enough information. I see no option for one player to miss a go. Can the coin played be used to push another coin, ie., to budge it up a bit, or are they notionally stuck to the table? Dependant on the rules there are several results, but the answer to the question, as posed, must be that it cannot be detrermined.
Got completly stumped by the fact that there were different amount of colored coins.. They should remove the picture or clarify the problem.
Hello, the image has been updated and the problem has been clarified. Sorry for the confusion!
If you put your first coin exactly in the middle of the table, then copy your friend's moves on the other side of the table, you'll get a guaranteed win. Since you will be copying your friend's moves, you will always have a place to put your coin if your friend does (since you're copying him), and when all the space is occupied, you will have placed the last coin.
What if only an even number of coins fit on the table, if you go first you will always have an odd number.
I took the easy way. Since no restriction was placed on the table size I looked at the case where the table diameter D < 3d, where d is the coin diameter. Player one puts the coin in the exact center and player two can't play. Game over. I like Michael Mendrin's solution though.
I also took this approach initially and then expanded the table diameter to see why the answer still held.
Let me summarize the comment section
In the very unlikely but possible case where the table is smaller than one coin; no one can put down anything, hence there is no winner.
The illustration is misleading, as according to the problem, it is impossible to have 9 orange and 7 blue at any point in the game.
Some say we can push the other player's coins so the problem is basically a circle packing problem, and for each table radius we need the parity of the maximal number of circles we can fit in to determine the winner.
Now a solution for the problem provided the table is sufficiently large and we can not push coins is: The starting player puts a coin in the middle of the table and then he puts his coins at the reflection (to the center of the table) of the second player's each turn. This way the starting player can place a coin iff the second player can place a coin. So the one who can not place a coin can not be the strating player. The starting player always wins.
Oh my god. Thanks for commenting.
The table being smaller than the coin is an invalid assumption. I don't want to use the picture argument or the common sense argument, but the question mentions that the first player places the first coin on the table, and the coin cannot go over the edge. So even by words it is already assumed that the table is bigger than the coin, and the first player wins every time if that is true, no matter the size of the table. The people raising that point are just being anal about getting it wrong or something
Second, it should be naturally assumed that you CAN'T push another coin. The question mentioned that you can only place a coin, and no dictionary definition of placing means pushing of any sort. If it can be pushed, why not push it over the table, since the current coin placed can't go over the edge, but it didn't say the past ones cant? Why not remove a coin since it didn't say you can't? Again on the point about people being anal. That is not even nitpicking on the right things.
The illustration is misleading though, and I think that's why they changed it. Now all the past comments about blue and orange coins are confusing as hell!
Based on the drawing, 17 coins can fit there. Since they're 2 players, and orange starts, then orange is coin n1 and blue is coin n2. Every coin with an even number is therefore blue, and every coin with an odd number is orange. 17 is odd, then it'll be an orange coin. Therefore, "me" wins. Simple!
you have less coins so that means you might have missed so either you went same number of times or you did less so its more likely its your turn
Recursive solution :
Start with the table being at the size of the coin : The first player wins.
By stretching one radius of the table, it follows that the other radii stretch too. Thus, when a radius has enough length so we can put a second coin, the radius on the
opposite side also has enough length so we can put a third coin and it goes on.
Since the maximum is always an odd number of coins, it follows that the first player wins.
PS : However it should also be precised that the table should at least have the size of one coin :p !
PS2 : This solution is also very nice since it helps answering a more general problem : if the first player puts n coins, the second n + k, then the first n + 2k..., assuming the table is saturated of coins at n + xk, who wins ?
I think the problem is not well structured; need further assumption(s) - the radius of the circular surface of the table must be divisible by the radius of a coin and the division must result in an odd integer. Without the assumption it is not conclusive that who will win.
Every position of the coin in the table has a symmetrical opposite position. Except one place which is the centre.
You begin by placing the first coin at the centre. After this, your opponent places his coin. You just have to place your coin it's opposite position till all places to fill are exhausted.
It is because he said that the last person who flips the coin wins while he said he was the first one to place a coin, they both placed 4 coins and all I did is to look at the second clue so the second clue was the answer
Since the size of the table has not been mentioned if we consider that the table is of the same size as that of the coin.....initially whoever places the coin will leave the second one with no place at all....in that way....whoever places the first coin wins (me in this case).
Can I say that, assuming both players play optimally then each play they make is the best possible one, then the one who on his first turn has more space to put a coin is the winner? I thought the whole problem of the game is: it's my turn and I don't have space to put my coin on the table, right? So on the first turn of "my friend" he has less options(space) than me. I will win because I'm playing in the best possible way but I start the game with a better scenario, so to speak.
What if you shift the coins so it's possible to squeeze in another coin in the created space? simular to this puzzle: https://www.youtube.com/watch?v=I-SpRl-AxI0
The 1st player puts the first coin in the exact center. Thereafter, wherever the 2nd player puts his coin, the 1st player puts a coin in the exact opposite place from the center. So, whenever there is a space for the 2nd player, the 1st player will have a space also. The 1st player is the one with a winning strategy.