Why excircles?

Geometry Level 5

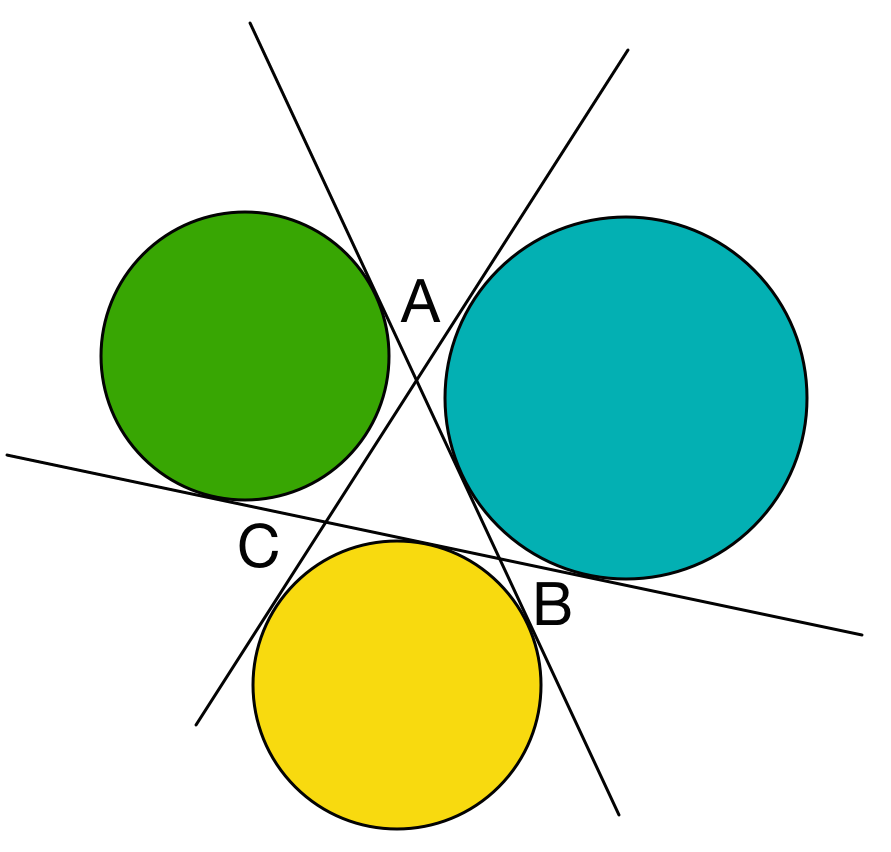
Let $I_1,I_2,I_3$ be the centres of the excircles of $\Delta ABC$ . Denote the area of $\Delta ABC$ by $\Delta_O$ and the area of $\Delta I_1I_2I_3$ by $\Delta_I$ .

Define the set $E$ as follows: $E=\left\{k\in \mathbb{R}\:|\:\Delta_I\geq k\Delta_O\: \text{for all triangles}\:\Delta ABC\right\}$

Enter the value of $\sup \{E\}$ up to three decimal places.

Notations:

$\sup$ denotes the supremum of a set.
$\mathbb{R}$ denotes the set of all real numbers.

This problem is part of my set: Geometry

The answer is 4.000.

2 solutions

Ameya Daigavane
Apr 7, 2016

If $I_1$ is the excentre opposite to $A$ , $AI_1 \perp AI_2, AI_1 \perp AI_3$ .
(The angle between internal and external angle bisectors is $\frac{\pi}{2}$ )

This means, $I_2 I_3$ passes through $A$ .
We conclude that the points $A, B, C$ lie on $\triangle I_1 I_2 I_3$ .
Now, from our first observation, $AI_1$ is in fact the altitude from $I_1$ to $I_2, I_3$ .
Thus, $\triangle ABC$ is the orthic triangle of $\triangle I_1 I_2 I_3$ .

From here, we can use the standard relations, to show that the ratio $\frac{\Delta_I}{\Delta_O}$ is at min $4$ .

Moderator note:

A more directly explanation for why $I_2 I_3$ passes through $A$ is that they lie on the exterior angle bisection of $A$ . This was already hinted at in your first sentence.

Exactly the intended solution! (+1)

A Former Brilliant Member - 5 years, 2 months ago

A bit more intensively we get the result via formula for the radii of the excircles giving the altitudes of the triangles that together with $\delta_{0}$ form $\delta_{I}$ .

Using the definition of E we consider triangel's inequalities which give us the possibility to perform a valuation for k upstairs finally resulting in: $k<=1+\frac{3}{1-\frac{c}{a+b}}$

From this we can conclude the maximum possible value (=Sup) k=4 since a+b>c must be fulfilled.

By the way: Very captious to wish the result "up to three decimal places"! ;-)

Andreas Wendler - 5 years, 2 months ago

Could you post it (with the details) as a solution?

Because I'm not getting what you're saying.

A Former Brilliant Member - 5 years, 2 months ago

@A Former Brilliant Member – $\Delta_{I}$ is constructed as the sum of $\Delta_{0}$ and the areas of 3 adjacent triangles each going through $I_{i}$ and having one side of the original triangle.

$\Delta_{I} = \Delta_{0} + \sum_{i=1}^{3} A_{i}$ with $A_{i}=0.5a_{i}r_{i}$

$r_{i}=\frac{ \Delta_{0}}{s-a_{i}}$ , $s=0.5\sum_{i=1}^{3}a_{i}$

Considering the definition of E it must be fulfilled:

$k<=1+0.5\sum_{i=1}^{3}\frac{a_{i}}{s-a_{i}}$

Now we have to find the minimum of the right side representing the supremum of k This is a problem of non-linear optimization whereat triangel's inequalities give restrictions. As result we find that all sides of ABC must be equal what denotes the equilateral triangle with $a_{i}=\frac{2}{3}s$ for i=1, 2, 3. Therefore sup{E}=4.

For numerical explanation we first express the sides of ABC in units of $a_{1}$ meanig we have sides 1, n, m and explore $f(n,m)=1+0.5(\frac{1}{s-1}+\frac{n}{s-n}+\frac{m}{s-m})$ for minimum. Triangle's inequalities restrict the allowed district defined by {(n, m): (0<n<=1 AND 1-n<m<1+n) OR (1<n AND n-1<m<n+1)}. We see that the borders have to be excluded!

Curves for f(n,m) mark f(1,1) = 4 as global minimum of f.

Andreas Wendler - 5 years, 2 months ago

@Andreas Wendler – OK. Just one thing, \Delta is displayed as $\Delta$ .

A Former Brilliant Member - 5 years, 2 months ago

@A Former Brilliant Member – Thanks and have a nice weekend!

Andreas Wendler - 5 years, 2 months ago

I think it's easier to understand the problem if we phrase it as "Find the infimium of $\{ \frac{ \Delta _I } { \Delta _O } \}$ taken over all triangles".

This avoid the multiple pharsing to understand the final question.

Calvin Lin Staff - 5 years, 2 months ago

I have not used $\dfrac{\Delta_I}{\Delta_O}$ as it might be undefined for degerate cases. For the question as it is, the answer is unchanged even if degerate cases are considered. However, if you insist, I'll change the statement.

Thanks for the image!

A Former Brilliant Member - 5 years, 2 months ago

what a simple solutions for a seemingly complicated problem, but i don't quite get why AI1 is perpendicular to AI2 and AI3, can you help me out? thanks!!!!!