Why this type of triangle has more properties?
Let
P
be an interior point of triangle
A
B
C
.
Let
Q
and
R
be the reflections of
P
in
A
B
and
A
C
, respectively.
If Q A R is a straight line, find ∠ B A C in degrees.
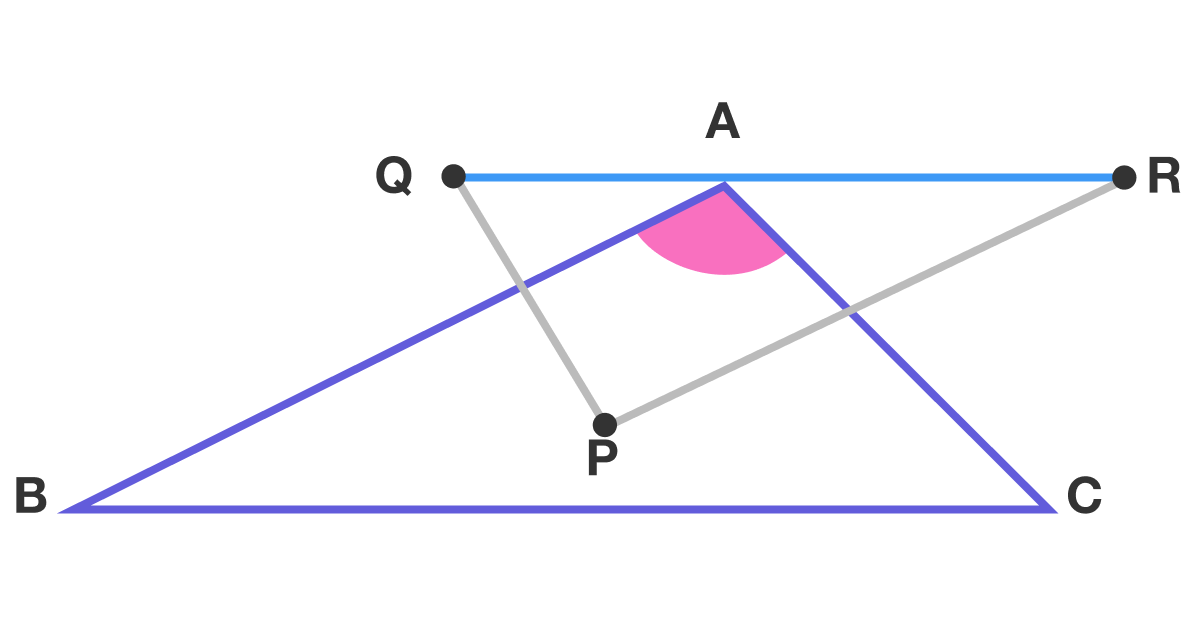
The image is not drawn to scale.
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
did the same
Did the same
Let the angle made by P A with A B and A C be α and β respectively.
Now, the fact that angle of incidence and angle of reflection are same shows that the following hold : ∠ P A Q = 2 α ∠ P A R = 2 β
As Q A R is a straight line, ∠ P A Q + ∠ P A R = 1 8 0 ∘ ⟹ ∠ A = α + β = 9 0 ∘
Can you please explain how you get ∠ P A Q = 2 α ? Thanks.
Log in to reply
This follows from the fact that angle of incidence is equal to the angle of reflection.
Log in to reply
It wold be better if this is mentioned in your solution.
Log in to reply
@Niranjan Khanderia – I've now added that justification.
Log in to reply
@A Former Brilliant Member – Thank you. It adds to the quality of solution.
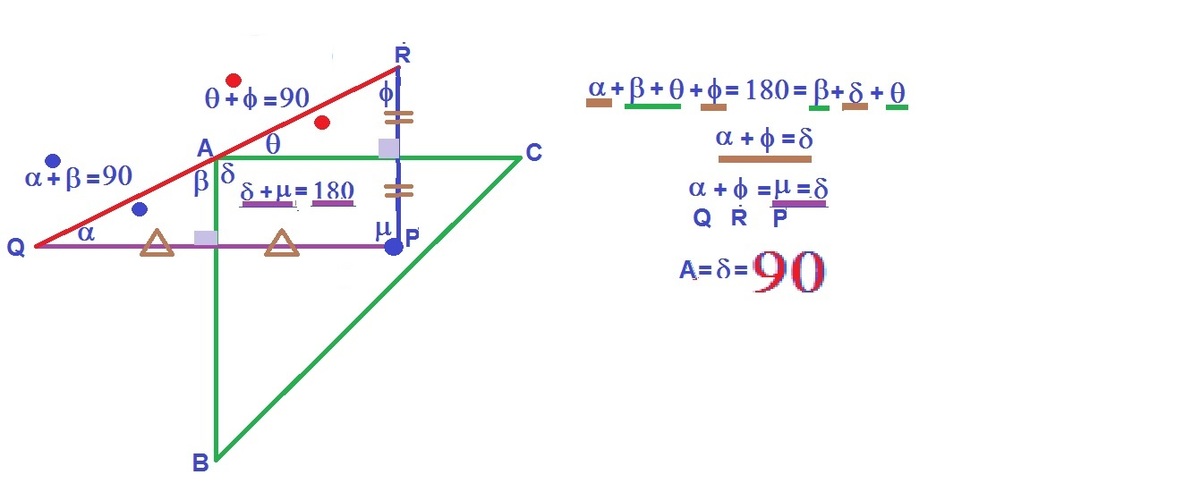
SOLUTION WITHOUT WORDS