Is Angle Chasing Useful?
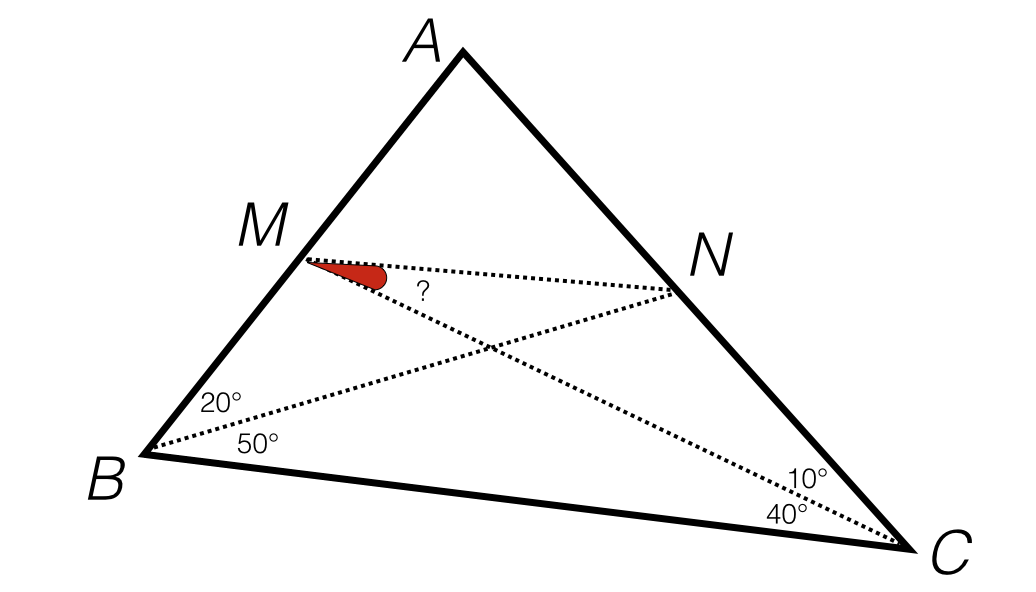
In triangle A B C , ∠ B = 7 0 ∘ and ∠ C = 5 0 ∘ . Point M is placed on side A B such that ∠ M C B = 4 0 ∘ and point N is placed on side A C such that ∠ N B C = 5 0 ∘ .
Find ∠ N M C (in degrees).
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Sir I m a moderate student of grade 8. it is difficult for me to understand without diagram. Therefore I request you to email me a diagram of your solution at [email protected] . I shall even be grateful to you for your act of kindness. Sir your little help can clear my concept.
I chased angles via trig. NB and CM turn out to be perpendicular (let's say they meet at O). I gave NC an arbitrary value of 10 (since I wasn't looking for lengths anyway, I was looking for a specific angle). I went counter clockwise through the (4) right triangles that meet at O.
Giving NC = 10, NO = 1.7365 and working thru to MO, MO = 3.0076.
Arctan NO/MO = 30 degrees.
How it can be NC = NM ??
Log in to reply
Oops. I gave NC the arbitrary value, I've corrected it.
Log in to reply
Sir, i don't think it's a right way to do so....because from your system the answer came 35.26 degree.....not 30 degree but its a nice and short way
Log in to reply
@Hassan Mahadi – I got 30 degrees exactly. I didn't show all of the similar trig ratios going around the four triangles meeting at O. But I did get exactly 30 degrees.
I liked your observation " NB and CM turn out to be perpendicular ". Your way of solution is out of the box. It is good to see such solutions.
I did this using trigonometry.
Let the lines B N and C M intersect at O . Now note that ∠ O C B = 4 0 ∘ and ∠ O B C = 5 0 ∘ . Hence ∠ B O C = 9 0 ∘ . i.e. lines M C and N B are perpendicular.
Let ∠ N M C = x . So we have tan x = M O N O , because △ N O M is a right triangle.
Similarly, from △ N O C we get, tan 1 0 ∘ = O C N O , and from △ M O B , we get tan 2 0 ∘ = O B M O . Finally from △ B O C , we have tan 4 0 ∘ = O C O B . Putting this all together we get:
tan 2 0 ∘ tan 1 0 ∘ = O B M O O C N O = M O N O O C O B = tan x tan 4 0 ∘
Hence, x = tan − 1 ( tan 2 0 ∘ tan 4 0 ∘ tan 1 0 ∘ )
Using a calculator, we get x = 3 0 ∘ .
Great solution.
Let angle NMC=x
Now angle BNC=80 and angle BMC=70
In triangle MNC:
MN/sin(10)=CN/sin(x)---------------------(1)
In triangle MNB:
MN=sin(20).BN/sin(70+x)----------------(2)
In triangle BNC:
BN=sin(50).BC/sin(80)----------------------(3)
From (2) and (3) we get
MN=sin(20).sin(50).BC/sin(80).sin(70+x)-----(4)
Again In triangle BNC:
CN=sin(50).BC/sin(80)-------------------------(5)
Now putting the value of MN and CN in equation (1)
sin(20).sin(50).BC/sin(10).sin(80).sin(70+x)=sin(50).BC/sin(80).sin(x)
or sin(20)/sin(10).sin(70+x)=1/sin(x)
or sin(20).sin(x)=sin(10).sin(70+x)
or 2sin(10).cos(10).sin(x)=sin(10).sin(70+x)
or 2cos(10)sin(x)=sin(70).cos(x)+cos(70).sin(x)
or sin(x)(2cos(10)-cos(70))=sin(70).cos(x)
or sin(x)/cos(x)=sin(70)/(2cos(10)-cos(70))
or tan(x)=0.57735027=1/sqrt(3)
or x=30 degree(ans)
∠ N B C = ∠ B C N , ∴ N B = N C . ∠ C M B = ∠ ( 1 8 0 − 2 0 − 5 0 − 4 0 ) = 7 0 . A p p l y i n g S i n L a w t o Δ s N M C a n d N M B , w e h a v e : − S i n ? S i n 1 0 = N C M N = N B M N = S i n ( 7 0 + ? ) S i n 2 0 O n e x p a n d i n g a n d r e a r r a n g i n g , S i n 1 0 S i n 2 0 = C o s 7 0 + S i n 7 0 C o t ? . ∴ C o t ? = S i n 7 0 S i n 1 0 S i n 2 0 − C o s 7 0 = 1 . 7 3 2 0 5 0 8 0 8 . ∴ ? = T a n − 1 1 . 7 3 2 0 5 0 8 0 8 1 = 3 0 o
Masbahul Islam's and my approach is the same. Use of Sin Law. His presentation is detailed and a little round about.
Let A'BC be the equilateral triangle. (A' is in the same side with A over BC).
Because ∠ N B C = 5 0 ∘ = ∠ C so N B = N C .
Because ∠ M C B = 4 0 ∘ so ∠ N C M = 1 0 ∘ = ∠ N B A ′ ( = 6 0 ∘ − 5 0 ∘ )
Because ∠ M C B = 4 0 ∘ so ∠ C M B = 7 0 ∘ = ∠ B , that leads to M C = B C = A ′ B
From the three above, we have △ A ′ B N = △ M C N so ∠ N M C = ∠ N A ′ B .
But because N B = N C and A'BC is an equilateral triangle so we can see ∠ N A ′ B = 3 0 ∘