Windows Calculator
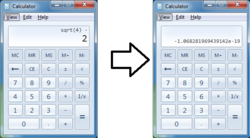I tried to find the value of
(
4
−
2
)
in my Windows calculator, and concluded that
4
<
4
. In which of these steps did I make a flaw in my logic?
Step 1 : The windows calculator evaluates that 4 − 2 = − 1 . 0 6 8 2 8 1 9 6 9 4 3 9 1 4 2 × 1 0 − 1 9 which is less than 0 . So we can conclude that:
4 − 2 < 0 .
Step 2 : Add 2 to both sides of the inequality to obtain:
4 < 2 .
Step 3 : Since both terms are positive, we can square both sides to obtain:
4 < 4
In which of these step did I make a flaw in my logic?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
It's how computers calculate. They calculate in binary and they're using special algorithms for caclulating. So you get something very, very close to 0, but not exactly 0.
Thus, Step 1 is wrong. You can't assume a calculator always gives the exactly value of an expression.
I just don't understand why this problem's an Algebra problem. It should be a problem of computer science.
Log in to reply
Thanks, I've edited this to CompSci
Log in to reply
Thank you.
Log in to reply
@Chung Kevin – Bro Might ur answer is right but Step 3 is always wrong... Squaring the numbers... l
but how can it be.. that this happens only when x − x type of expression is input ?
Log in to reply
Computers represent integers exactly, but they cannot represent all floating-point numbers exactly. x is computed numerically as a floating-point number. So, the result of x − x is a floating-point number.
Note that it does not only happen with x . For example, sin ( 9 0 ) − 1 and lo g ( 1 0 ) − 1 are also computed inexactly.
Right! The problem is flot number.
Symbolic computation done by Google or Wolfram Alpha gives you the right answer, zero.
I disagree that step 1 is a logical fallacy. It's earlier than that; it's a problem with the calculator. If the calculator was giving a correct output, then step 1 would be an entirely logical deduction. This is why I answered 'None of these choices'. Apparently my answer is wrong. I don't think so. Consider if the mathematician had completed an identical argument by calculating sqrt(3) - 2. The argument would be entirely valid, including step 1. It's what happens before step 1 that is invalid.
Log in to reply
I'm with you, deriving from the axiom that the numerical bug in the windows calculator is right, everything is pretty logical, and like those here said, float point calculation is not exactly precise.
Either way, you can still know that
1.
4
=
±
2
, not 2
2.
∣
4
∣
−
2
=
0
.
Ergo, this step is wrong, regardless of the medium of calculation.
Log in to reply
Sqrt of any number is always positive.
Rightly said and I also marked Step 3 thinking the same
Sqrt of any real number is positive
That did not format well! Do you want to try again Eric?
Log in to reply
@Martin Gibbs – OK, looking at the Latex formatting, I'm guessing you're trying to say that the square root symbol means plus or minus the square root. No, it doesn't. The square root sign applied to positive real numbers means the principal square root, i.e. the positive one. I'll try to use Latex formatting to demonstrate what I mean, but I've never used it before.
Log in to reply
@Martin Gibbs
–
4
=
2
±
4
=
±
2
4
=
−
2
Log in to reply
@Martin Gibbs – Well, the formatting isn't working at all. Experienced users, is this because I need to install some extension for my browser or something? Or is it because we're doing it wrong? Rishabh's solution at the top displays fine, but Eric and my posts look awful. Are they displaying for other people?
Log in to reply
@Martin Gibbs – Anyway, the third paragraph of this: http://en.wikipedia.org/wiki/Square_root and this http://mathworld.wolfram.com/SquareRoot.html refute what I think you're saying Eric.
This is not a very good problem. I do not understand why it was posted.
Log in to reply
I think it proved to be somewhat useful 'cause I didn't even know that this happens in windows calculator and many others would have also not known.
Log in to reply
I would understand if it was posted as a note, but not a problem.
Log in to reply
@Colin Carmody – yeah.. that could have been done. Anyway I got something new and that's what I need. :)
@Colin Carmody – If it isn't a very good logic question, then why have only 44% gotten it right? This is a great troubleshooting question. And good for teaching not to simply accept the data as presented
Log in to reply
@Christopher Giddens – Probably because they thought it was a trick question, but it wasn't. It is my opinion that it is not a good problem, but if you beg to differ, I will not argue.
@Christopher Giddens – Some of us disagree with the 'correct' answer. See my earlier post.
Agreed. This is CompSci, not Maths.
How to replicate this behavior:
a) Press 4 then √ then - then 2. Enter.
b) Press 4 then √ then -. Enter.
I am not sure what is going on here. My guess is that it's a bug.
Interesting bug. The computer thinks that the square root of 4 is 2 in the second problem, thus the answer is 2-2 or 0
Sqrt(4) = 2; thus 2-2 should be 0.
The answer to Sqrt(4) - 2 according to Excel is 0.
Log in to reply
The value would greatly depend on which calculator you are using, and the degree of accuracy that you put it in.
My windows calculator was giving the value as
4 − 2 = − 8 . 1 6 4 8 4 6 5 9 5 5 5 1 4 2 8 7 1 6 8 5 2 1 1 8 0 1 2 2 9 2 8 × 1 0 − 3 9
I don't get how this value is coming
But, on putting -
4 − 2 = − 8 . 1 6 4 8 4 6 5 9 5 5 5 1 4 2 8 7 1 6 8 5 2 1 1 8 0 1 2 2 9 2 8 × 1 0 − 3 9
4 = 2 + ( − 8 . 1 6 4 8 4 6 5 9 5 5 5 1 4 2 8 7 1 6 8 5 2 1 1 8 0 1 2 2 9 2 8 × 1 0 − 3 9
4 = 2 (It is the value given by calculator.)
So, 4 = 4