WMC 2018 Senior Problem 3
True or False?
The sum a + b + c varies depending on the location of P .
Clarification : Point P lies inside of this equilateral triangle, at perpendicular distances a , b , and c from the sides of the triangle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Dennis Engel October 15, 2018
Consider the given position of point P.
Extend the normal b by an amount d to point P’. From P’ drop perpendiculars onto the other two normal lines.
Inspection of the triangles formed shows that a and c are each reduced by d cos60 = ½ d. The sum of the changes in length of b, a and c is: 1 – 2(½ d) = 0. Therefore the sum a + b + c is constant.
Log in to reply
Doesn't this only work for when PP' is perpendicular to the side of the triangle?
The answer Of FALSE only accounts for a 2 dimensional triangle on a flat plane with only 2 dimensions (x, y). If you were to move point P up or down a Z axis in a 3 deminsonal grid (x, y, z), the answer would then be TRUE. But these kinds of criteria are never accounted for or specified/eliminated when questions are asked on here. They tried by saying clarification, point P lies inside the equilateral triangle, but technically (depending on your viewpoint) P can still be inside the equilateral triangle even when the Z axis is changed which will make that sum of a+b+c vary.
Log in to reply
Christopher -- Doesn't the term 'triangle' explicitly imply a two-dimensional geometric figure ?
What if the triangle was not Equilateral? What would be the condition under this would be?
Log in to reply
Then condition is not true, try to draw some triangles and measure the distances.
This is also a theorem known as Viviani's Theorem , which states that the sum of the distances from any point in the interior of an equilateral triangle is in fact the length of the altitude of the triangle.
It the image, a, b and c look like the distance between P and the triangle side, not the area.
Log in to reply
I think you commented on the wrong solution...
The area calculation was used to get an expression for a+b+c ... which turns out to be a constant based on the triangle’s side length.
Let the side length of the equilateral triangle be s . Then the area of the triangle is A △ = 2 1 s ( a + b + c ) . Since the area of the triangle A △ is the same wherever P is, therefore, a + b + c must be a constant.
False , the sum a + b + c does not depend on the location of P .
This answer is great on so many levels. Upvoted.
A[triangle] = 1/2 sa + 1/2 sb + 1'2 sc = 1/2 s (a + b + c). From there, go to Chew-Seong Cheong proof above.
Better proof and more simplistic and intuitive.
Indeed it's true for any regular n − gon and the required sum of distances is given by a 2 × S , where a and S respectively denote the area and side of the n − gon or, equivalently n × r , where r = inradius of the circle inscribed in the n − gon Q . E . D
There is a typo in the first formula: it should be S 2 × a . Great generalization anyway!
Consider three very long lines which meet at P at 120 degrees, one line being vertical. So we have a Y-shape. Now place an equilateral triangle with a horizontal base over this so that P is enclosed (and the three original lines extend beyond the three sides of the triangle). The three lines segments inside the triangle are the a, b and c in the question. As in the question, let b be vertical. Let a + b + c = k. Now, if the triangle is shifted parallel to any of its sides, let's pick the horizontal one and shift right, b will remain unchanged. This will make a shorter and c longer by equal amounts (simple geometry). So a' + b' + c' = k again. This shifting process can be repeated parallel to any of the three sides to create all possible formulations of the problem. Therefore, in all situations, a + b + c = k where k is constant.
A great visual proof of the problem (Viviani's theorem): https://youtu.be/uf2ChRpFTZk
Connect the point with the three corners. You will get three triangles forming the big triangle. let h be the height of the big triangle.
So its area is 2 1 ⋅ h ⋅ s and the added area of the three small triangles is 2 1 ⋅ a ⋅ s + 2 1 ⋅ b ⋅ s + 2 1 ⋅ c ⋅ s .
Therefore 2 1 ⋅ h ⋅ s = 2 1 ⋅ a ⋅ s + 2 1 ⋅ b ⋅ s + 2 1 ⋅ c ⋅ s
and so 2 1 ⋅ h ⋅ s = 2 1 ⋅ s ⋅ ( a + b + c ) and h = a + b + c So the sum of a,b and c is always equal to the height of the triangle .
Drawing lines from the point P out to each of the vertices, three triangles are created whose areas make up the area of the original equilateral triangle. Each of the perpendicular distances a, b, and c can be seen as the height of each of the new triangles created. Because the bases of each of these new triangles remains constant (as well as the 1/2 component of the area formula), their areas are only changed with a change in their height (represented by a, b, or c). Using the fact that the sum of these areas must always equal the original area of the equilateral triangle and that the bases of the triangles remain constant, a + b + c must always remain constant. Else, the area of the triangles would not fill out the original triangle correctly.
Let l be a line perpendicular to the segment of length b that contains P . Notice that, if we move P along l , the lengths a and c vary linearly , which implies the sum a + c also does. However, notice that there is a point where the lengths of a and c ``swap'' with relation to their original position, that is, there are two different positions of P where a + c is the same, implying that a + c is constant when P is moved along l . Since the length b does not vary at all in this process, the sum a + b + c is preserved. An analogous reasoning can be applied to demonstrate that, for any line perpendicular to any of the three segments that contains P , moving the point along that line preserves the sum.
Finally, notice that, for any position inside the triangle, it is possible to relocate P to that position by successive movements along such perpendicular lines (move the point along one line, adjust the positions of the lines, move again). That implies that, for any possible position of P , the sum a + b + c is constant.
Hopefully my reasoning is clear enough. If need be, I can get more formal.
I think it would be helpful if the problem made it a little more clear which of the two statements we are asking about.
What "two statements"?
Log in to reply
Nevermind... The problem has been changed since I made that comment.
Log in to reply
Yeah, i thought that was the case... Do you remember what were those previous statements? ;-)
Log in to reply
@C . – Previously, the clarification at the bottom looked more like a second statement... ;)
Consider the extremes. As line segment a approaches bisecting the equilateral triangle into two 30-60-90 triangles, it is twice the length of b or c when a approaches zero.
Connect the vertices of the triangle to point P . Now the area of the Larger Triangle is sum of the areas of the smaller 3 Triangles . But the area of smaller triangles is 1/2 base times altitude . Assuming the base to be B( side of the Equilateral Triangle ) , the area of the Equilateral triangle is 1/2 x B x ( a+b+c ) . Now regardless of the location of point P , the base B and area of the Equilateral Triangle stays the same and hence a+b+c has to be constant . Hope it was short and sweet .
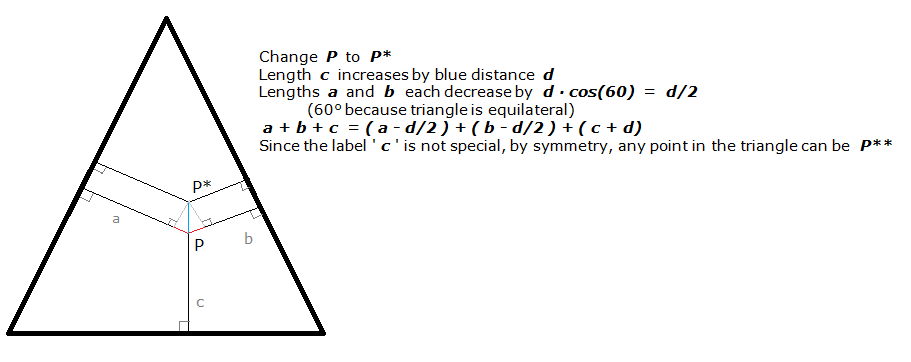
Let the side length of the triangle be s . Then its area is 4 s 2 3 .
The sum of the areas of the red, green, and blue triangles is:
2 1 s a + 2 1 s b + 2 1 s c = 2 1 s ( a + b + c ) = 4 s 2 3
Therefore, a + b + c = 2 s 3 , which will not vary based on the location of point P .