Woodworking
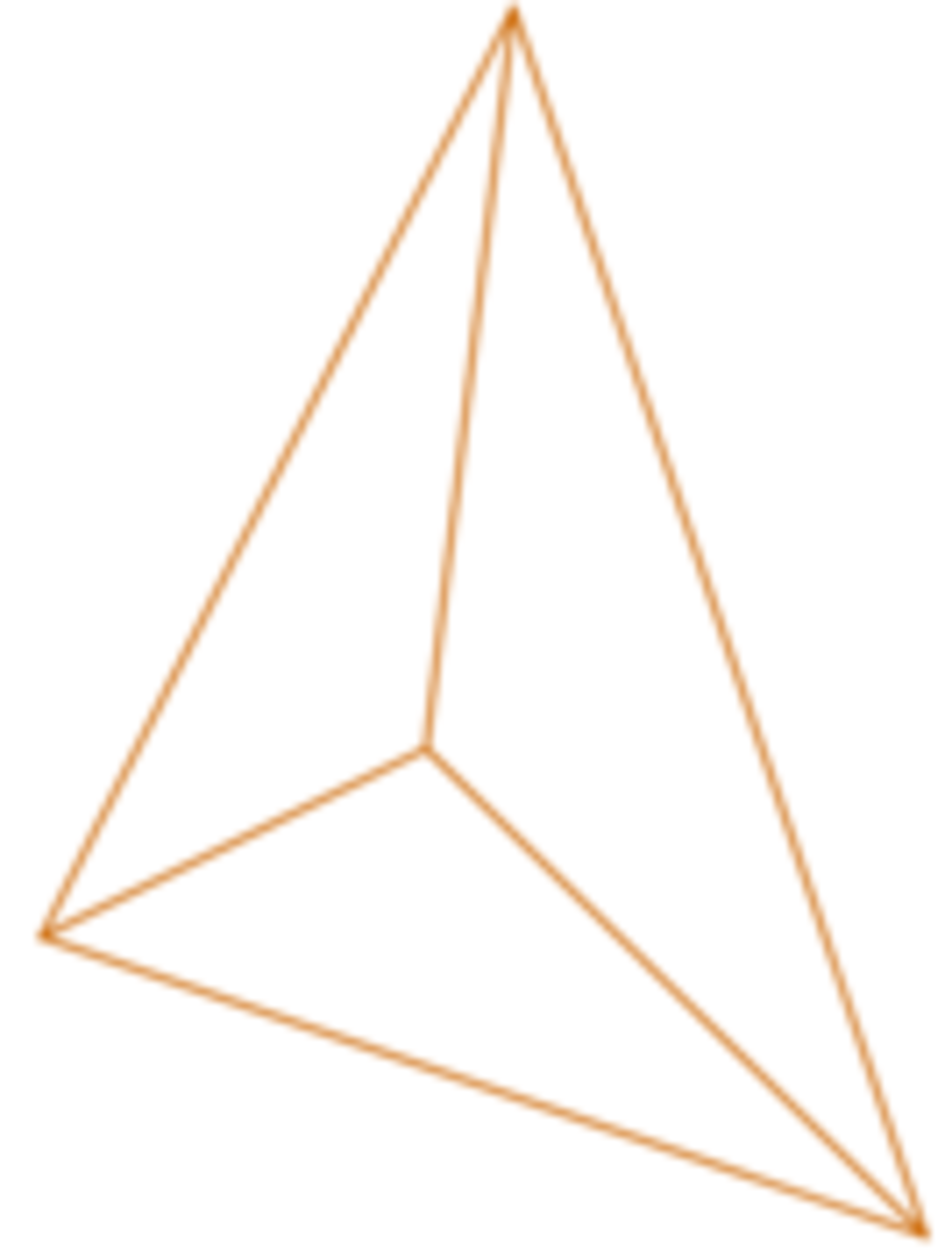
A person finds a piece of wood in a shape of irregular tetrahedron with base edges of length: 5, 6, 7 cm and the remaining three edges of length 8 cm.
Because the surface of the wooden block is damaged, the person decides to take 0.5 cm off each face of the tetrahedron. After doing so, he notices further damage near the vertices of the tetrahedron so he decides to make a sphere shape. What is the radius r of the largest sphere he can make of the remaining wooden block?
Submit your answer as ⌊ 1 0 0 0 0 r ⌋ .
Try also Woodworks II
The answer is 7968.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since V is the volume of the tetrahedron and S A is the surface area, shouldn't the formula for the inradius be S A 3 V ? This is what you must have used to get the answer. The volume of a tetrahedron is 3 1 × base × height, and so the volume of the tetrahedron is the sum of 3 1 r A , where A is the area of each of the faces and r is the inradius, in other words the volume is 3 1 r S A .
Log in to reply
Thank you. I corrected the typo in the solution.
I kept thinking there was some subtle trickery involved in shaving off that 0.5 cm from the faces.
It would be interesting to do a proper proof for that. I think it would be equivalent to proving that original solid and the shaved one are similar.
Just found something interesting. The inradius formula for any solid is the same. Further read can be found here .
Log in to reply
The link you posted is bad. Try again. here
However, it should be pointed out that finding the inradius of a solid depends on all of its faces being tangent to the insphere. That's not always the case. Think of an ordinary shoebox.
Log in to reply
One time I did not check a link and got a bad one; fixed now. The author uses a term "CIRCUMSOLIDS", which would not apply to a shoebox.
I just did more thorough checking of the result, working face by face, and it looks correct to me.
Log in to reply
@Maria Kozlowska – Oh, I don't have any doubt that your answer is correct, it's just that you made me think two or three times to make sure I wasn't falling into some kind of a trap.
Insphere is the largest sphere that can fit inside a given tetrahedron. First we are going to calculate radius of the insphere of the original tetrahedron. The formula is given as
r = S A 3 V
where S A is a Surface Area and V = 3 ! 1 2 3 1 d e t ( 1 , 0 a i j 2 , 1 )
a i j denotes an edge connecting vertex A i and A j and
d e t ( 1 , 0 a i j 2 , 1 ) = d e t ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 0 a 1 , 2 2 a 1 , 3 2 a 1 , 4 2 1 a 1 , 2 2 0 a 2 , 3 2 a 2 , 4 2 1 a 1 , 3 2 a 2 , 3 2 0 a 3 , 4 2 1 a 1 , 4 2 a 2 , 4 2 a 3 , 4 2 0 1 1 1 1 1 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎞
Our determinant:
d e t ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 0 8 2 8 2 8 2 1 8 2 0 5 2 6 2 1 8 2 5 2 0 7 2 1 8 2 6 2 7 2 0 1 1 1 1 1 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎞ = 3 5 4 1 6 8
which gives volume of 4 9 1 9 / 2 .
S A ≈ 8 1 . 1 2 2 0 0 4 6 0 7 3 4
r ≈ 1 . 2 9 6 8 5 3 7 3 2 5 9 5
After removing 0 . 5 cm off each face the insphere's radius will be:
r 2 = r − 0 . 5 ≈ 0 . 7 9 6 8 5 3 7 3 2 5 9 5 .
The answer is 7 9 6 8 .