Like poison chocolate...

Probability Level 1

The coin can only be moved up, left, or diagonally up-and-left.

Charlie and Tracy are playing a game on a $5 \times 3$ grid with a coin in its lower right corner. The rules are as follows:

Charlie goes first, then they take turns moving the coin.
The coin can only be moved one space up, left, or diagonally up-and-left.
The first one to move the coin to the upper left corner wins.

If both play optimally, who will always win?

Charlie Tracy Either player can win

13 solutions

David Vreken
Jul 29, 2018

Any player who can move his or her coin in either of the blue or red squares (colored below) will win the game.

This is because if Player A moves his or her coin to a blue square, then the only way to move afterwards is to move up, so Player B must move to a white square, Player A must move to a blue square, and so on, until Player A wins the game. Likewise, if Player A moves his or her coin to the red square, then the only way to move afterwards is to move left, so Player B must move to the white square to the left of it, and Player A will move to the to the winning square and win the game.

Therefore at the beginning of the game, the optimal strategy would be to avoid moving into the second column, because then the opponent can move to one of the blue squares and win the game. So each player should choose to move up.

This strategy is fine until someone (in this case, Charlie) must move off of the green square. Then no matter which of the possible squares he moves to, the other player (Tracy) can move to either a blue, purple, or red square and then win the game.

So if both play optimally, Tracy will always win the game.

I think it would good to state explicitly in the problem that a move can only go one step in any of the three allowed directions. So a player only gets to pick the direction, but not the length, of his/her next move.

Matthew Feig - 2 years, 10 months ago

Indeed. Charlie wins by moving the coin up three steps.

Willem Monsuwe - 2 years, 10 months ago

Although I didn't interpret the problem in this way, I think your reply clearly illustrates why the one step-requirement is necessary.

Roland van Vliembergen - 2 years, 10 months ago

@Roland van Vliembergen – One reason I interpreted it this way is because I recently watched a video from James Grime (singingbanana) on a game isomorphic to Wythoff's Game. (Short version: One queen, chessboard, only left and/or down, alternate moves, move into corner wins)

Willem Monsuwe - 2 years, 9 months ago

Generalization:

Claim. For $m \times n$ grid, if either $m$ or $n$ is even, the first player is guaranteed to win if play optimally; if both $m$ and $n$ are odd, then the second player is guaranteed to win if play optimally.

Proof. Let me first prove that if both $m$ and $n$ are odd, then the second player is guaranteed to win.

For each $m \times n$ grid, players have to move $m-1$ spaces up and $n-1$ spaces left and the winner is the one who first comes to the point $(m,n)$ . Since players are allowed to move by one space in either one or both directions and if $m-1$ and $n-1$ are both even (ie. $m$ and $n$ are both odd), then the second player has an advantage because he can always correct the parity and return it to even again until $m-1 = 0$ and $n-1 = 0$ when he's the winner. He does this "correction" by mimicking the move of the first player.

If either $m$ or $n$ is even, the first player can always do such a move to set the parity to odd-odd. Now, he becomes the second to play with $m$ and $n$ both odd, a situation where he is guaranteed to win as we shown above.

Uros Stojkovic - 2 years, 10 months ago

Uros -- In the second paragraph of Proof. don't you mean 'n-1 spaces left' instead of 'n-1 spaces right' ? The coin is initially at the bottom right corner of the grid and the players are moving it to the top left corner.

Jesse Otis - 2 years, 10 months ago

Yes, I do. Thanks for pointing that out to me.

Uros Stojkovic - 2 years, 10 months ago

Jeremy Galvagni
Jul 29, 2018

If you start your turn on an L you will lose because you can only move to a W If you start your turn on a W you will win because it's possible to move to an L. (The upper left has an L because if the counter is there after your opponent moved, you have lost.) Since the starting square has an L, Charlie will lose, Tracy will win.

Edited to fix the picture. I did it right on paper but drew it wrong in Paint. Thanks, GU and CM for your corrections.

You have mislabeled some squares. If you are in the centre square, you can move the coin left and force the other player to lose.

Chris Maitland - 2 years, 10 months ago

While the idea is right, the winning and losing squares are wrongly labeled. If the position of starting square is (1; 1) and for the winning one is (3;5), then losing squares are only (1; 1), (3; 1), (1; 3), (3; 3), (1;5). For example, (2;1) is not losing because you can move to (3; 1).

Gediminas Usevičius - 2 years, 10 months ago

I took a similar approach to yours. I marked the winning square as W and employed the following rules for each square: If it's possible to reach a W or a 0 in one move, mark it as a 1. Otherwise, mark it as a 0. Using this you can work up and get a similar pattern to yours, and you can tell if your square is winning based on if it's a 1 or a 0, marking the one who starts in the bottom right to lose.

Simeon Widdis - 2 years, 10 months ago

Nice. I made a follow-up to this that will be a featured problem for the coming week. I hope you enjoy it.

Jeremy Galvagni - 2 years, 10 months ago

Carlos Higuera
Jul 29, 2018

There are three possible number of moves, depending on the number of diagonal moves used:

Game Moves	4	5	6
Diagonal Moves	0	1	2
1st Turn	C	C	C
2nd Turn	T	T	T
3rd Turn	C	C	C
4th Turn	T	T	T
5th Turn		C	C
6th Turn			T

Charlie will only win if exactly 1 diagonal move is used in the game. He can't make his first move diagonally since this would allow Tracy to move diagonally again, finishing the game with 2 diagonal moves. He also can't move left because this would allow Tracey to move left again (hitting the wall), which would block any diagonal moves for the rest of the game. This forces him to always play upwards. Tracy can't move left or diagonally because this will allow Charlie to finish the game with 1 diagonal move. So she can only move upwards. This repeats until they arrive at the top right square, at which point they can only go left, making the total number of moves 6 and hence Tracy wins.

Your row Diagonal Moves should go from 2 down to 0, if I'm correct? RIght now it says 1,2,3 which makes no sense given the text below, and given the problem. 0, 1, or 2 diagonal moves can be used, and the more diagonal moves occur, the shorter the game is.

Roland van Vliembergen - 2 years, 10 months ago

You're right, thanks for pointing that out

Carlos Higuera - 2 years, 10 months ago

you can get it in 5 moves by going diagonal left up up up so either player can win

Seth Colquhoun - 2 years, 10 months ago

Interliser 727
Jul 24, 2018

The answer is quite simple. Just move the coin into the white boxes as below.

Kaelyn Willingham
Aug 2, 2018

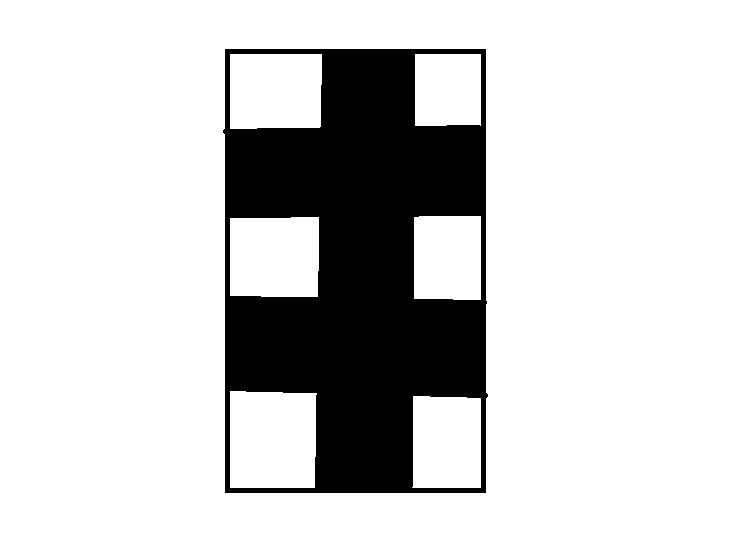
The optimal path from lower-right to upper-left corner is by taking the shortest path. In this case, that would be moving along a diagonal, then taking 2 moves up. This path requires 4 individual moves, which means Tracy will always win since she takes the even-numbered moves (2 & 4).

Maroš Paliga
Jul 31, 2018

Longest route is even. So Charlie cant afford to prolong as much as possible. Therefore he must do shortcut by diagonal move in which case Tracy gonna do the same and finish on even again.

Stewart Gordon
Aug 5, 2018

Whatever move Charlie pays, Tracy can just copy it (i.e. move by the same vector). With the small number of possibilities, it's easy to see that this process will eventually lead to the top left corner on Tracy's move.

Ervyn Manuyag
Aug 1, 2018

Try playing it with a friend

Arousse Fares
Jul 31, 2018

We can do it backwards :

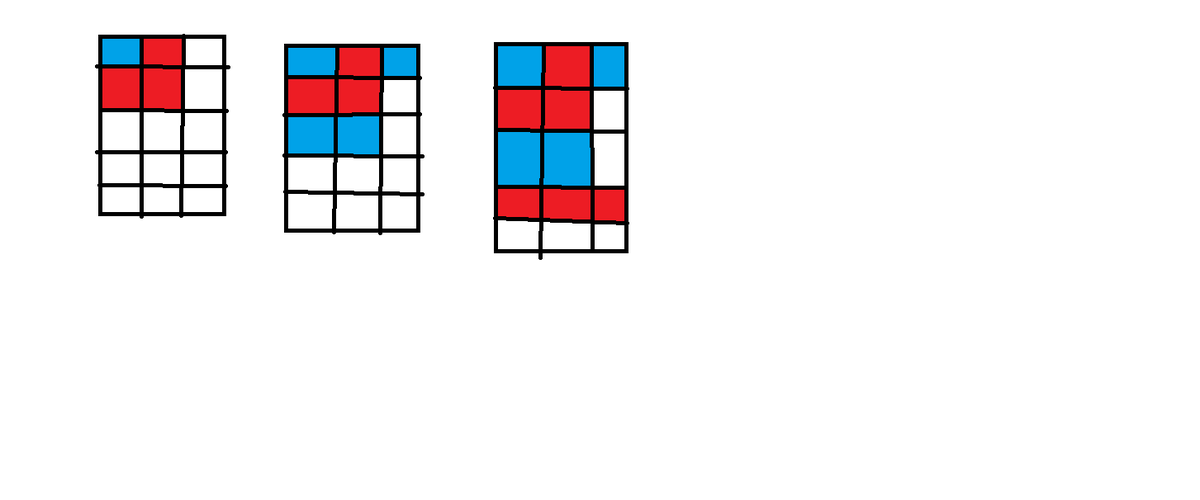
Step 1 : If it's your turn and you go to a red square, you loose.

Step 2 : If it's your turn and you go to a blue square, you win.

Step 3 : If it's your turn and you go to a red square, you loose. But since player 2 can force player 1 to go to one of those red squares, player 2 wins !!

Here is a little variant : What would happen if you take away the square on the bottom left ? Awesome, right ? :D

A Former Brilliant Member
Jul 30, 2018

The simplest way to understand this is economic rather than mathematic. Anyone who starts always has a +1 'effect' on the game, or in other words modifies the grid relative to the other player by -1 square each time.

Vinod Kumar
Jul 30, 2018

For Player A to win, he has to reach the target in odd number of steps, however, Player B is able to force A to cover it in even number of steps in all the three options. Thus, Player B wins in all the three options.

Bart Meijer
Jul 30, 2018

If the number of moves from start to finish is even, Tracy wins. By moving diagonally, Tracy can make sure this number is always even.

Hoh Shu Hao
Jul 30, 2018

If you reach the top left tile you win, by counting the number of moves back you can deduce that Tracy will always win.

Like poison chocolate...

13 solutions

0 pending reports