Would You Like a Cube With That?
a 3 + b 3 = 2 5 9 3 0 8 0 , a + b = 2 1 0 , a b = ?
The answer is 10584.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Moderator note:
Nice use of colours to visualize your work. Splendid!
Nice solution! upvoted!
There is another way to solve this, it is as follows.
we know that, ( a + b ) 3 = a 3 + b 3 + 3 a b ( a + b )
Substituting the values in the equation above we get, ( 2 1 0 ) 3 = 2 5 9 3 0 8 0 + 3 a b ( 2 1 0 )
Or, 9 2 6 1 0 0 0 − 2 5 9 3 0 8 0 = 3 a b ( 2 1 0 )
Or, 6 6 6 7 9 2 0 = 3 a b ( 2 1 0 )
Or, 3 a b = 2 1 0 6 6 6 7 9 2 0 = 3 1 7 5 2
Or, a b = 3 3 1 7 5 2
Or, a b = 1 0 5 8 4
Moderator note:
Nice way of isolating the variables. Great work!
G r e a t !
Log in to reply
Thank you!
Sir, Please take this suggestion, do press enter twice so that the solution looks good. Thank you!
Log in to reply
T h a n k y o u v e r y m u c h f o r s u g g e s t i o n !
who give you the permission to put or we use or only for either connection . if ab=0 then either a=0 or b=0 but in this case or can't work so replace it with implies inorder to get the logic is correct
I did something similar. Good work.
Where did 9261000 come from?
a 3 + b 3 ⇒ 2 5 9 3 0 8 0 ⇒ a b = ( a + b ) ( a 2 + b 2 − a b ) = ( a + b ) [ ( a + b ) 2 − 2 a b − a b ] = ( a + b ) [ ( a + b ) 2 − 3 a b ] = 2 1 0 ( 2 1 0 2 − 3 a b ) = 3 1 ( 2 1 0 2 − 2 1 0 2 5 9 3 0 8 0 ) = 3 4 4 1 0 0 − 1 2 3 4 8 = 3 3 1 7 5 2 = 1 0 5 8 4
Moderator note:
Yes, the conventional sum of two cubes identity works too. Nicely done!
Good solution sir! upvoted!
the solution is very simple based on the factorization of a 3 + b 3
so as we know that a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) , keep in your mind we
need a + b and not a − b so we will add − 2 a b + 2 a b = 0 to the second term to get :
a 3 + b 3 = ( a + b ) ( a 2 + 2 a b − 2 a b − a b + b 2 )
by using ( a + b ) 2 = a 2 + b 2 + 2 a b
we obtain a 3 + b 3 = ( a + b ) ( ( a + b ) 2 − 3 a b )
back word substitution to get :
2 5 9 3 0 8 0 = ( 2 1 0 ) ( ( 2 1 0 ) 2 − 3 a b )
thus 1 2 3 4 8 = 4 4 1 0 0 − 3 a b
therefore a b = − 3 1 2 3 8 4 − 4 4 1 0 0 = 1 0 5 8 4
a 3 + b 3 = ( a + b ) ( a 2 + 2 a b + b 2 )
2 5 9 3 0 8 0 = ( a + b ) ( a 2 + 2 a b + b 2 )
2 5 9 3 0 8 0 = ( 1 2 0 ) ( a 2 + 2 a b + b 2 )
1 2 3 4 8 = ( a 2 + 2 a b + b 2 ) − − − ( 1 )
We know that
( a + b ) 2 = a 2 + 2 a b + b 2
a 2 + 2 a b + b 2 = 2 1 0 ∗ 2 1 0 = 4 4 1 0 0 − − − ( 2 )
Use systems of linear Equation on (1) and (2)
3 a b = 3 1 7 5 2
a b = 1 0 5 8 4
Moderator note:
Concise and correct!
Typo: In lines 1 through 4, you should replace 2 a b with − a b .
Typo: On line 3 replace 120 with 210.
a^2 + b^2 + 2 a b = 210^2 ................... (1)
a^2 + b^2- a b = 2593080/210 ..........(2)
(1) - (2)
3 a b = 31752
a b = 10584
Identity: a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 )
2 5 9 3 0 8 0 = 2 1 0 ( a 2 − a b + b 2 )
2 1 0 2 5 9 3 0 8 0 = a 2 − a b + b 2
My own derived identity: ( a + b ) 2 − 3 a b = 2 1 0 2 − 3 a b = a 2 + 2 a b + b 2 − 3 a b = a 2 − a b + b 2
Substitute:
2 1 0 2 5 9 3 0 8 0 = 2 1 0 2 − 3 a b
3 a b = 3 1 7 5 2
a b = 1 0 5 8 4
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 )
2 5 9 3 0 8 0 = ( 2 1 0 ) ( a 2 − a b + b 2 )
1 2 3 4 8 = a 2 − a b + b 2
a b = ( a 2 + b 2 ) − 1 2 3 4 8
In order to solve the problem, you'll need to get the value of a 2 + b 2 . We know that,
( a + b ) 2 = a 2 + 2 a b + b 2
4 4 1 0 0 = a 2 + 2 a b + b 2
4 4 1 0 0 − 2 a b = a 2 + b 2
Now substitute the value of a 2 + b 2 to the equation.
a b = ( 4 4 1 0 0 − 2 a b ) − 1 2 3 4 8
3 a b = 3 1 7 5 2
a b = 1 0 5 8 4
nicely solved.
Dk why the number are so big (needed to use a calculator (T-T))
You can do it by hand using long division.
Why cannot a and b have other values?
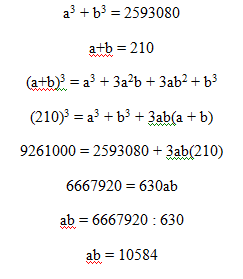
a 3 + b 3 = 2 5 9 3 0 8 0 a + b = 2 1 0 a 3 + b 3 = 2 5 9 3 0 8 0
( a + b ) ( a 2 − a b + b 2 ) = 2 5 9 3 0 8 0
( 2 1 0 ) ( a 2 − a b + b 2 ) = 2 5 9 3 0 8 0
a 2 − a b + b 2 = 1 2 3 4 8
a 2 − a b + 3 a b + b 2 = 1 2 3 4 8 + 3 a b
a 2 + 2 a b + b 2 = 1 2 3 4 8 + 3 a b
( a + b ) 2 = 1 2 3 4 8 + 3 a b
2 1 0 2 = 1 2 3 4 8 + 3 a b
4 4 1 0 0 = 1 2 3 4 8 + 3 a b
3 1 7 5 2 = 3 a b
a b = 1 0 5 8 4